 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Момент импульса. Пусть материальная точка массой движется со скоростью относительно точки О, а
Пусть материальная точка массой 
движется со скоростью 
относительно точки О, а 
радиус-вектор этой материальной точки, проведённый из точки О (рис. 3.9).
Определение. Моментом импульса материальной точки относительно точки О называется векторное произведение радиуса-вектора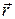 
на вектор импульса 
:
Направление 
перпендикулярно плоскости, в которой лежат векторы 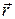и 
, в соответствии с правилом правого винта, например момент импульса электрона, двигающегося по круговой орбите в боровской модели атома.
Свяжем момент импульса с моментом инерции и угловой скоростью. Пусть радиус-вектор 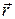некоторой частицы массой лежит в плоскости рис. 3.10, скорость перпендикулярна ей («от нас»), частица движется по окружности радиусом 
.
Модуль момента импульса 
. Линейную скорость 
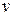можно связать с угловой 
относительно оси 
как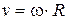 
, тогда 
. Проекция вектора на ось вращения равна
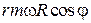. Как видно из рис. 3.10, 
, т.е.
Для системы материальных точек (твёрдого тела) выражение связ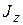и 
, 
и формально такое, как и для материальной точки:
Но под 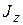здесь подразумевается сумма моментов инерции материальных точек системы:
Можно показать (см., например, в [1]), что для однородного тела, симметричного относительно оси вращения, суммарный момент импульса тела 
. Он направлен вдоль оси вращения в ту же сторону, что и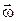 
, т.е.
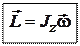
(Для несимметричного тела в общем случае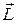 
не совпадает по направлению с вектором ).
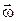5. Уравнение моментов. В дальнейших преобразованиях условимся для упрощения записи индекс 0 у ,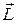 
и других величин не писать, но подразумевать, что он есть.
Продифференцируем выражение для момента импульса материальной точки: 
. 
.
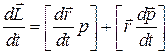Учтём, что 
, а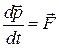 
.
Рассмотрим первое слагаемое (см. в лекции № 1 «Векторное произведение»).
= 
(так как угол между и 
равен нулю).
Второе слагаемое в выражении для 
(по определению момента силы).
В результате получаем:
Уравнение моментов (оно связывает момент импульса с моментом силы).
Производная по времени момента импульса материальной точки относительно точки О равна моменту действующей силы относительно точки О.
Поиск по сайту: