АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Уравнение моментов для твёрдого тела

Читайте также:
  1. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  2. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  3. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона
  4. Волна вероятности. Уравнение Шредингера
  5. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  6. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЁРДОГО ТЕЛА
  7. Временное и стационарное уравнение Шредингера. Решения.
  8. Вязкость жидкости. Уравнение Ньютона. Закон Пуазейля
  9. Гармонические колебания и их характеристики. Дифференциальное уравнение свободных гармонических колебаний.
  10. Гипербола. Каноническое уравнение гиперболы и его свойства.
  11. Давление газа с точки зрения молекулярно-кинетической теории. Уравнение состояния идеального газа.
  12. Давление газа. Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона). Изопроцессы.

Рассмотрим систему частиц, на которую действуют как внутренние, так внешние силы. Моментом импульса 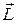системы относительно точки О называется сумма моментов импульса 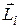отдельных частиц 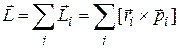. Дифференцирование по времени даёт, что

.

Для каждой из частиц можно написать уравнение моментов

,

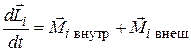где 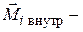момент внутренних сил, а 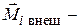момент внешних сил, действующих на -ю частицу. 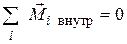(по 3-му закону Ньютона, так как внутренние силы образуют пары, равные по величине, противоположные по направлению и действующие вдоль одной прямой, т.е. образуют равные по величине и противоположно направленные моменты сил).

Получаем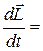

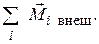
Обозначим 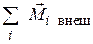= 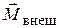, получаем окончательно

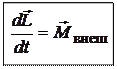
Производная по времени от момента импульса механической системы относительно некоторой точки О равна суммарному моменту относительно той же точки всех внешних сил, приложенных к системе (уравнение моментов).


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)