ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ

План

1. Первый закон Ньютона и понятие инерциальной системы отсчёта.

2. Второй закон Ньютона как уравнение движения. Понятия массы, силы, импульса.

3. Третий закон Ньютона и пределы его применения.

4. Неинерциальные системы отсчёта. Абсолютные и относительные скорости и ускорения. Силы инерции (центробежная сила и сила Кориолиса).

5. Центр инерции (центр масс). Теорема о движении центра инерции.

1. 1-й закон Ньютона. Материальная точка, не подверженная внешним воздействиям, либо находится в покое, либо движется равномерно и прямолинейно. Такое тело называется свободным,его движение – свободным движением, или движением по инерции.

Классическая механика постулирует, что существует система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно. Такая система называется инерциальной системой отсчёта. Таким образом, 1-й закон Ньютона выражает критерий инерциальности системы отсчёта.

2. 2-й закон Ньютона. Производная импульса материальной точки по времени равна действующей на неё силе.

где – импульс (количество движения), векторная величина, равная для материальной точки произведению её массы на скорость и направленная вдоль ;

– масса – мера инертности тел.

Импульс механической системы равен геометрической сумме импульсов всех точек системы.

Сила в механике – мера механического действия на данное материальное тело других тел. Это действие может иметь место как при непосредственном контакте, так и через посредство создаваемых телами полей (электромагнитным, полем тяготения). Сила – величина векторная и в каждый момент времени характеризуется численным значением, направлением в пространстве и точкой приложения. Сложение сил производится по правилу параллелограмма. В современной физике различают 4 вида взаимодействий:

1) гравитационное (обусловлено всемирным тяготением);

2) электромагнитное (осуществляется через электрические и магнитные поля);

3) сильное, или ядерное (обеспечивающее связь частиц в атомном ядре);

4) слабое (ответственное за многие процессы распада элементарных частиц).

Пример использования 2-го закона Ньютона как уравнения движения:

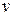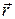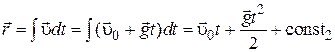Дано: , , .	Решение: , , , . При , , , , , . При , , , .
Найти:

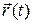
3. 3-й закон Ньютона. Силы взаимодействия двух материальных точек равны по величине, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки.

Третий закон, как и 1-й и 2-й, справедливы лишь в инерциальных системах отсчёта. Кроме того, отступление от 3-го закона наблюдается в случае движения тел со скоростями, сравнимыми со скоростью света.

В случае движущихся зарядов необходимо учитывать также взаимодействие с магнитными полями, создаваемыми ими. Пусть два положительных заряда и двигаются со скоростями и (рис. 2.1). На каждый заряд со стороны другого действует как кулоновская , так и лоренцева силы . Направления векторов индукции магнитных полей и 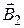, создаваемых частицами и , определяются по правилу правого винта (буравчика).

Рис. 2.1

Магнитные силы Лоренца и не совпадают по направлению. Результирующие силы и не равны друг другу и не направлены противоположно.

4. Неинерциальные системы отсчёта. Силы инерции. Изобразим две системы отсчёта, из которых К является инерциальной, а система движется относительно К с некоторым ускорением и, следовательно, неинерциальная (рис. 2.2).

Рис. 2.2

В случае, когда система движется относительно К поступательно:

где радиус-вектор точки m в системе К; радиус-вектор начала координат ; радиус-вектор точки m в системе . Продифференцируем дважды выражение :

,

,

где 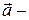ускорение частицы m в системе К;

– ускорение начала системы относительно системы К;

– ускорение частицы в системе .

; умножим обе части этого уравнения на m, получим

, здесь по 2-му закону Ньютона сила, действующая на частицу со стороны других тел , тогда:

То есть относительно системы частица ведёт себя так, как если бы кроме силы на нее действует дополнительная сила . Эта сила называется силой инерции.

Движение относительно выбранной условно неподвижной системы называется абсолютным. Вектор даёт абсолютную скорость, абсолютное ускорение, а и относительные скорость и ускорение.

Поиск по сайту: