Таблицы перегретого пара

В табл. III приведены термодинамические свойства воды и перегретого пара. По этим таблицам для заданных давлений и температур можно найти удельный объем, энтальпию и энтропию однофазной среды – воды и перегретого пара.

В первом столбце указаны температуры перегретого пара, расположенные в порядке их возрастания, начиная от 0 до 1000 ^оС. Для каждой температуры даются значения v, h и s, расположенные в последующих столбцах при различных давлениях перегретого пара.В строках по горизонтали указаны давления начиная от 1 кПа до 100 МПа. Таким образом, эта таблица дает возможность непосредственно или интерполяцией найти значения указанных в ней параметров, не прибегая к вычислениям.

По табл. IV можно определить истинную массовую изобарную теплоемкость воды и водяного пара в зависимости от давления и температуры. В табл. V определяется скорость звука в воде и водяном паре. Пользуясь табл. VI, можно определить поверхностное натяжение воды σ, изобарную теплоемкость , теплопроводность λ, динамическую вязкость µ, число Прандтля Pr для воды и пара в состоянии насыщения. В табл.VII–IX определяется динамическая вязкость µ, теплопроводность λ и число Прандтля Pr воды и водяного пара.

Рис. 6.4. Термодинамические свойства воды и перегретого пара

6.3. sT- диаграмма

Для изображения в системе sT- координат процесса парообразования необходимо пользоваться такими соотношениями для этого процесса, которые были бы выражены через параметры s и Т. При построении sT- диаграммы для первой стадии парообразования – нагрева 1 кг воды от 0 ^оС до температуры кипения – пользуются уравнением:

, (6.1)

в котором Т ≤ 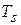и s ≤ .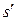

Если Т равно 273 К (т.е. 0 ^оС), как видно из уравнения, s = 0 и, следовательно, точка, определяющая это состояние воды, должна лежать на оси ординат. Обозначим эту точку через А (рис. 6.1).

Рис. 6.1. Изображение процесса парообразования при постоянном давлении

в осях sТ

Если воду подогреть до температуры, положим, Т ₁, то энтропия, увеличиваясь, станет равной s ₁, и состояние воды будет определяться точкой 1. Если подогреть воду больше, то температура ее будет возрастать, принимая значения Т ₂, Т ₃ и т.д. до температуры 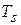, когда вода начнет кипеть. При этом энтропия воды будет также все время увеличиваться и принимать значения соответственно s ₂, s ₃и, наконец, s’ (при температуре, равной ).

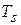Состояние пара при указанных значениях температуры и энтропии будет на диаграмме определяться точками 2, 3 и т.д. точкой В. Если через все эти точки провести плавную кривую, то она будет графически изображать характер изменения энтропии при нагревании воды от 0 ^оС до .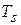

При дальнейшем подводе теплоты вода начнет превращаться в пар, энтропия будет продолжать увеличиваться, но температура не будет изменяться, поэтому линия процесса для этой стадии парообразования изобразится в виде прямой ВС, параллельной оси абсцисс. Точка С определяет состояние, в котором вся вода превратилась в пар (состояние сухого пара). Изменение энтропии в процессе парообразования, т.е. от точки В до точки С, может быть подсчитано по уравнению

. (6.2)

При дальнейшем подводе теплоты пар перейдет в область перегрева, при этом будут возрастать энтропия и температура его. Линия процесса для данной стадии парообразования CD строится по уравнению

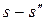= 2,3 lg . (6.3)

Таким образом, весь процесс получения перегретого пара изобразится ломаной линией ABCD.

Значение энтропии пара в точке С может быть подсчитано по уравнению

. (6.4)

Изменение энтропии изобразится на диаграмме суммой отрезков и ВС; следовательно,

ВС, (6,5)

откуда следует, что

ВС = . (6.6)

Если процесс парообразования не доводить до конца, т.е. остановиться на какой-нибудь точке Е, которая будет определять состояние влажного пара степени сухости х, то изменение энтропии можно подсчитать по уравнению

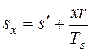. (6.7)

На диаграмме

ВЕ, (6.8)

откуда следует, что

ВЕ = . (6.9)

Деля уравнение (6.9) на уравнение (6.6), получим

= х.

Следовательно, отношение равно степени сухости пара. Если повысить давление воды, из которой был получен перегретый пар, то очевидно, что при температуре, соответствующей точке В, кипение еще не наступит; для того чтобы вода закипела, ее необходимо подогреть до более высокой температуры, при этом увеличится и энтропия. Момент начала кипения определится точкой , расположенной на продолжении линии АВ, а состояние сухого пара – (рис. 6.2).

Если же давление воды понизить, то момент начала кипения изобразится какой-нибудь точкой В ₁, лежащей также на прямой АВ, но ниже точки В. При этом давлении состояние сухого пара изобразится точкой С ₁.

Беря разные значения давлений воды, получим ряд точек: В ₁, В ₂, В ₃ и т.д., соответствующих началу кипения воды, и ряд точек: С ₁, С ₂, С ₃ и т.д., соответствующих состоянию сухого пара. Если через эти точки провести плавные линии, то на диаграмме получатся две кривые АК и DК: первая из них будет являться кривой жидкости, разделяющей области жидкости и влажного насыщенного пара, разделяющей области влажного и перегретого паров. Как видно на чертеже, эти линии сходятся и точка пересечения их, очевидно, является критической точкой К, о которой уже говорилось раньше.

Если на линиях ВС, В ₁ С ₁, В ₂ С ₂ и т.д. нанести точки Е, Е ₁, Е ₂, Е ₃ и т.д., соответствующие какому-нибудь значению степени сухости, и провести через них плавную кривую, то получим так называемую линию постоянной степени сухости (или постоянного паросодержания) КЕ ₄.

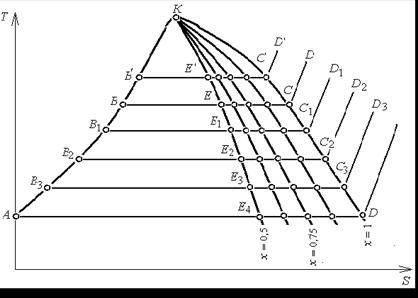
Рис. 6.2. sT ― диаграмма водяного пара (схема)

Таких линий для различных значений степени сухости можно нанести на диаграмме несколько; тогда получим ряд кривых, также сходящихся в критической точке.

В sT -диаграмме площадь, ограниченная линией процесса, осью абсцисс и крайними ординатами, определяет количество теплоты, участвующей в процессе. Применим это свойство sT -диаграммы к процессу парообразования, который изобразим линией Ааbс (рис. 6.3).

Процесс превращения кипящей воды в пар при этом изобразится линией ab. Согласно указанному свойству площадь прямоугольника abmn должна определять теплоту парообразования r. Действительно, для конечной точки этого процесса – точки b, когда пар превратится в сухой, значение энтропии находят по уравнению:

.

Откуда

.

Рис. 6.3. Изображение в осях sT теплоты в процессе парообразования

На рис. 6.3 значение температуры 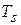определяется отрезком an, т.е. высотой прямоугольника abmn, а 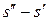– отрезком nm, равным основанию этого прямоугольника.

Для других стадий парообразования площадь 0 Aan определяет количество теплоты , которое требуется подвести к воде, взятой при 0 ^оС, чтобы довести ее до кипения, а площадь mbcf – количество теплоты, затрачиваемый на перегрев.

Понятно, что сумма площадей 0 Aan и nabm представляет величину полной теплоты сухого пара . Если же к эти двум площадям прибавить еще и площадь mbcf, то получим графическое изображение величины полной теплоты перегретого пара λ. Для влажного пара, состояние которого определяется, например, точкой е, теплота будет равна сумме площадей 0 Aan и naet. Обратное протекание процесса от точки с к точке А связано с уменьшением энтропии, а следовательно, и с отводом теплоты от рабочего тела. При этом указанные площади будут представлять собой количества отведенной теплоты.

6.4. hs- диаграмма

sT- диаграмма является очень наглядной при различных исследованиях, связанных с теплотой. Однако в расчетной работе эта диаграмма неудобна тем, что для нахождения по ней количества теплоты, участвующей в процессе, нужно измерять площадь. В тех случаях, когда линия процесса является кривой, это представляет некоторые затруднения. Поэтому в теплотехнических расчетах часто пользуются диаграммой, в которой по оси ординат отложены величины энтальпии, а по оси абсцисс – изменение энтропии. Для того чтобы найти величину энтальпии по такой диаграмме, а следовательно, и количество теплоты, необходимо измерить лишь длину соответствующего отрезка по оси ординат, что, конечно, гораздо проще, чем измерять площадь. Эта диаграмма получила название
si- диаграммы.

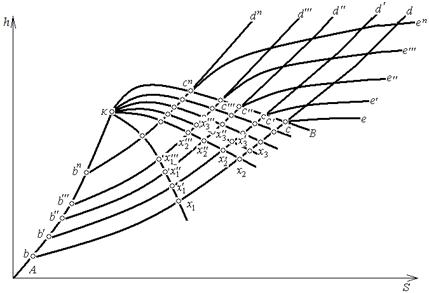
Рис. 6.4. si- диаграмма водяного пара (схема)

На нее наносятся обычно те же линии, что и в sT -диаграмме, т.е. кривые жидкости и сухого насыщенного пара, линии постоянных давлений и линии постоянных степеней сухости. Кроме того, на si- диаграмме наносятся линии постоянных температур, которые в sT -диаграмме имеют вид горизонтальных линий. АК – линия жидкости, КВ – линия сухого пара.

На практике обычно не приходится иметь дела с очень влажными парами, область которых находится в нижней части si- диаграммы. Поэтому для практических целей пользуются только правой верхней ее частью, что дает возможность выполнить ее в более крупном масштабе и сделать более подробной и удобной для пользования. Такая диаграмма построена профессором Вукаловичем.

Поиск по сайту: