Ексудат контролювати

При планировании перевозок возникает необходимость в определении кратчайших расстояний между АТП, пунктами производства и потребления, местами тяготения пассажиров и т.д. Кроме того кратчайшие расстояния являются основой при оплате клиентами транспортных услуг. Они необходимы также для определения грузооборота АТП, учета расхода топлива, расчета заработной платы водителей.

Для нахождения оптимального решения используются математические методы, при применении которых необходима в качестве исходных данных транспортная сеть, отражающая транспортные связи между точками города (местности). Множество всех дорог города (района) составляют дорожную сеть, но понятие транспортной сети несколько уже в ней учитываются только те улицы и дороги которые пригодны для движения по ширине проезжей части и качеству покрытия. Модель такой сети может быть представлена в виде графа.

Граф – это фигура, состоящая из точек (вершин) и отрезков (ребер) их соединяющих.Ребра характеризуются числами, которые могут иметь различный физический смысл (расстояние, время движения в мин., стоимость проезда и т.д.).

Рис.1

Ребра, ориентированные по направлению называются дугами. Всякое не ориентированное ребро включает две равноценные дуги. В зависимости от того все или часть ребер имеют направление, граф является ориентированным или смешанным. Существует ряд различных математических методов для определения кратчайших расстояний. Некоторые из них требуют применения ЭВМ, есть и доступные ручному расчету.

Рис. 2.

На любом этапе определения кратчайших расстояний от заданной вершины все множество вершин разбивается на три группы:

1). Вершины до которых кратчайшие расстояния уже найдены.

2). Вершины смежные с вершинами первой группы.

3). Все остальные.

Решение задачи состоит из нескольких этапов:

1). Выбирается вершина из первой группы с минимальным кратчайшим расстоянием от начального.

2). Определяются расстояния до неё от смежных с ней вершин.

3). Вершина с минимальным кратчайшим расстоянием переводится из группы 2 в группу 1.

4). По завершении определения всех кратчайших расстояний лишние связи из графа убираются.

ДАЛЕЕ ЗАДАЧА 1 и 2.

Основные понятия теории вероятности, используемые в задачах моделирования движения автомобилей.

Из основных понятий теории вероятности, прежде всего, рассматривается событие и его количественная характеристика (вероятность события). Под событием понимается любой факт, который может произойти, либо не произойти, в результате некоторого эксперимента, опыта или наблюдения при осуществлении определенного комплекса условий.

Например, время безотказной работы двигателя можно считать событием, прибытие автомобиля к перекрестку и т.д. Чтобы количественно сравнить между собой события по их степени возможности нужно с каждым событием связать определенное число, которое тем больше, чем более возможно само событие. Таким числом является вероятность события, которую отождествляют с опытным понятием относительной частоты или частости. Частость события называют статической вероятностью и определяют по формуле:

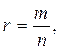
где m – число появлений исследуемого события,

n – общее число произведенных опытов.

Например из нескольких участков продольного профиля автодорог с твердым покрытием, проходящих по резко пересеченной местности выбирается один и определяется количество элементов с постоянным уклоном В результате подсчета выявлено, что из общего количества различных уклонов равного 200 уклоны встречались 28 раз.

частость.

Частость события носит случайный характер и может заметно изменяться от одной группы опытов к другой. Однако при увеличении числа опытов частость события проявляет тенденцию стабилизироваться.

Таким образом, в качестве экспериментальной характеристики любого события естественно принимать его относительную частоту, представляющую собой отношение числа опытов, в которых данное событие появилось к числу всех произведенных опытов.

Для достоверного события, т.е. события которое обязательно происходит в результате опыта частость равна 1. Для невозможного события частость равна 0. Характерное для каждого события число около которого стремится стабилизироваться частость события при большом числе опытов называется вероятностью события.

Фундаментальным в теории вероятности является понятие случайной величины, играющей большую роль в приложениях. Случайной называется величина, которая в результате опыта может принять то или иное, но только одно значение, причем заранее неизвестное. Поскольку в теории вероятности и математической статистики оперируют массовыми явлениями, то случайная величина характеризуется возможными значениями и вероятностями этих значений. В практики выделяют два основных типа случайных величин дискретные и непрерывные. Дискретными называют случайные величины, которые принимают только отделенные друг от друга значения, причем можно их заранее перечислить. Например, количество автомобилей на заданном участке дороги может принимать только целочисленные значения 1,2,3 и т.д.,для дорог 1 категории уклоны могут принимать значения ,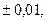

а для дорог 2 категории, еще, т.е. принимают значения кратные 0,01, которые можно рассматривать как целочисленные.

Чаще встречаются случайные величины другого типа – непрерывные, которые играют исключительно важную роль в технических приложениях. Непрерывной случайной величиной называется такая возможные значения которой непрерывно заполняют некоторый промежуток (интервал числовой оси). Очевидно, что интервал может быть конечным или бесконечным. Например, углы открытия водителем дроссельной заслонки карбюратора, скорость движения автомобиля на заданном участке, ошибки измерений относят к непрерывным случайным величинам.

Случайные величины обозначаются заглавными буквами латинского алфавита, а их возможные значения соответствующими маленькими буквами:

Пусть событие А – наличие на автодороге дискретного значения уклона равного 0,06. Тогда вероятность этого события Р(А). Если продолжительность проезда по заданному участку дороги характеризовать непрерывной случайной величиной Т, то запись Р(0,8<T<1) будет читаться как вероятность того, что автомобиль будет преодолевать участок дороги за время от 0,8 до 1 часа.

Формы представления закона распределения случайной величины могут быть различными. Простейшей формой задания закона распределения случайной величины Х является ряд распределения или таблица вероятных значений:

Чтобы ряд распределения дискретных случайных величин имел более наглядный вид его часто изображают графически. С этой целью откладывают по оси абсцисс все возможные значения случайных величин, а по оси ординат соответствующие вероятность.

Для непрерывной случайной величины ряд распределений вообще построить нельзя. Это вызвано тем, что непрерывная случайная величина характеризуется бесчисленным множеством возможных значений, которые заполняют некоторый промежуток. Однако различные диапазоны возможных значений случайной величины являются неодинаково вероятными и для непрерывной случайной величины существует распределение не конкретных значений, а величин интервалов.

Более наглядное представление о характере распределения непрерывной случайной величины в окрестности различных точек дает функция, которая называется плотностью распределения вероятности. Плотностью распределения случайной величины в точке является предел отношения вероятности попадания непрерывной случайной величины на элементарный участок от х до х+ х к длине этого участка, когда последняя стремится к нулю.

Плотность распределения f(x) указывает на то как часто появляется случайная величина в некоторой окрестности точки Х при многократном повторении опытов. Кривая изображающая плотность распределения случайной величины называется кривой распределения.

Для количественной характеристики распределения непрерывной случайной величины используют вероятность события Р(X<x). Вероятность этого события является какой-то функцией распределения случайной величины F(x)=P(X<x), где F(x) называется интегральной функцией распределения или интегральным законом распределения.

При решении многих практических задач часто возникает необходимость указать только отдельные числовые параметры называемые числовыми характеристиками случайной величины и характеризующие существенные особенности того или иного распределения. О каждой случайной величине необходимо знать ее некоторое среднее значение, около которого группируется возможное значение случайной величины или степень разбросанности этих значений относительного среднего. Важнейшей числовой характеристикой, определяющей положение случайной величины на числовой оси, является математическое ожидание М[x]=a, которое иногда называют средним значением случайной величины.

Для дискретной случайной величины Х математическое ожидание определяется как:

Следовательно математическое ожидание для дискретной случайной величины есть сумма произведений возможных значений на их вероятности.

Для непрерывной случайной величины:

Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Для дискретной случайной величины:

Для непрерывной случайной величины: .

В практике часто используется другая числовая характеристика случайной величины – среднее квадратическое отклонение:

Каждое исследование в области случайных явлений связано с экспериментом, опытными или статистическими данными. Разработка методов регистрации, описания и анализа экспериментальных данных, получаемых в результате наблюдений массовых явлений составляет предмет прикладной науки – математическую статистику, которая дополняет теорию вероятности. Одной из основных задач математической статистики является определение закона распределения случайной величины. Она включает следующие этапы:

1). Представление экспериментальных или статистических данных в форме статистического ряда.

2). Определение параметров закона распределения.

3). Проверка согласия теоретического и статистического распределения по критерию Пирсона

4). Построение графика теоретической кривой распределения, если это необходимо.

При моделировании движения автомобиля с использованием метода статистических испытаний применяют различные законы распределения случайных величин. Для наиболее распространенного нормального закона возможными значениями случайной величины являются все действительные числа как положительные, так и отрицательные. Кривые плотности вероятности нормально распределенной случайной величины симметричны относительно ординаты в точке x=a=M[X].

Нормальный закон распределения имеет место практически во всех случаях, в которых случайная величина Х образуется в результате суммирования очень большого числа случайных величин одного порядка малости.

Моделирование находит применение во всех отраслях инженерной деятельности и в первую очередь в следующих ее областях: проектирование систем и их составных частей; планирование и анализ функционирования существующих систем; инженерный анализ и обработка информации; управление динамическими системами.

В основе детерменированных моделей лежит функциональная зависимость между отдельными показателями, например, скоростью и дистанцией между автомобилями в потоке. В стохастических моделях транспортный поток рассматривается как вероятностный процесс.

Все модели транспортных потоков можно разбить на три класса: модели-аналоги, модели следования за лидером и вероятностные модели. В моделях-аналогах движение транспортных средств уподобляется какому-либо физическому потоку (гидро- и газодинамические модели).

В моделях следования за лидером существенно наличие связи между перемещениями ведомого и головного автомобиля. По мере развития теории в моделях этой группы учитывалось время реакции водителя, исследовалось движение на многополосных дорогах, изучалась устойчивость движения.

В вероятностных моделях транспортный поток рассматривается как результат взаимодействия транспортных средств на элементах транспортной сети. В связи с жестким характером ограничений сети и массовым характером движения в транспортном потоке складываются отчетливые закономерности формирования очередей, интервалов загрузок по полосам дороги и т.д.

Закон сохранения транспортного потока

Рассмотрим поток транспорта на однополосной дороге, то есть при движении без обгонов. Плотность автомобилей в момент времени t обозначим q. Число автомобилей в интервале (S_1;S₂) в момент времени t равно: qdS.

Пусть v – скорость автомобилей в точке S в момент t.Число проходящих через S (единицу длины) автомобилей в момент t есть qv. Найдем уравнение изменения плотности. Число автомобилей в интервале (S₁;S₂) за время t изменяется в соответствии с числом въезжающих и выезжающих автомобилей:

(1)

Интегрируя по времени и полагая, что q и v – непрерывные функции, получим .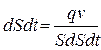

Поскольку S₁, S₂, t₁, t₂>0 произвольны получим (2).

Найдем уравнение для скорости v. Положим, что v зависит только от плотности q. Если дорога пуста (q=0), то автомобили едут с максимальной скоростью v_max. При наполнении дороги скорость падает вплоть до полной остановки (v=0), когда автомобили расположены «бампер-к-бамперу» (q=q_max). Эта простейшая модель выражается следующим линейным соотношением

.

Тогда уравнение (2) примет вид:

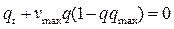. (3)

Очевидно, что это закон сохранения количества автомобилей. Интегрируя (3) по S получим:

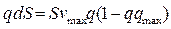
Следовательно количество автомобилей постоянно для любых значений t.

Основы статистической обработки результатов наблюдения.

Часто при проведении каких-либо исследований, например, при измерении скорости движения автомобилей в транспортном потоке, получают ряд числовых значений изучаемой изучаемого параметра, величину которых нельзя предсказать заранее исходя из условий эксперимента.

Установление закономерностей, которым подчиняются массовые случайные явления, основано на изучении статистических данных, т.е. сведений о том какие значения принял в результате наблюдений интересующий параметр.

Статистическая обработка начинается с установления шкалы интервалов в соответствии с которой группируются результаты наблюдений. Для определения оптимальной величины интервала, при которой построенный интервальный ряд не был бы слишком громоздким и в тоже время позволял выявить характерные черты изучаемого явления, можно использовать формулу Стерджеса, в соответствии с которой:

где N – общее число наблюдений.

Если h оказывается дробным числом, то за величину интервала следует взять либо ближайшее целое число, либо ближайшую несложную дробь. За начало первого интервала рекомендуется принимать величину равную 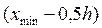. Тогда начало следующего интервала будет: . Построение интервалов продолжается до тех пор, пока начало следующего по порядку интервала не будет равным или большем . После установления шкалы интервалов приступают к группировке результатов наблюдений. Обычно все вычисления в математической статистике проводят в табличной форме, которая более удобна, т.к. позволяет проверять вычисления на каждом этапе благодаря своей наглядности.

Интервал значений	Средний интервал	Частота	Частость ,%	Накопленная частость ,%

Средние значения в интервалах необходимы для того, чтобы заменить интервальный ряд дискретным и в дальнейшем использовать зависимости применяемые при обработке дискретных случайных величин.

Частость:

Накопленная частость.

Определяется как последовательная сумма частостей каждого интервала. По данным таблицы строят гистограмму, полигон, кумулятивную кривую, которые являются графическим изображением статистического ряда. Они позволяют в наглядной форме представить основные закономерности изменения значений исследуемого параметра.

Гистограмма служит для изображения только интервального статистического ряда. Для её построений по оси абсцисс откладывают отрезки, изображающие интервалы варьирования и на этих отрезках как на основании строят прямоугольники с высотами равными частости.

Полигон служит для изображения как дискретных, так и интервальных статистических рядов. Для его построения в прямоугольной системе координат наносят точки с координатами 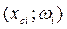и последовательно соединяют.

Кумулятивная кривая строится в прямоугольной системе координат. По оси абсцисс откладывают интервалы, а по оси ординат значения накопленной частости. Построив кумулятивную кривую можно приблизительно установить число элементов ряда, для которых значения параметра меньше или равно данному числу.

Если выборка имеет приближенно нормальный закон распределения, то справедливо следующее выражение:

где САО – среднее абсолютное отклонение,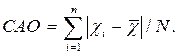

Задача стр.23.Есть выборка из 100 значений мгновенных скоростей автомобилей, движущихся в потоке. Необходимо определить средние скорости потока, медленно едущих автомобилей, автомобилей двигающихся со скоростью выше средней скорости потока. Определить числовые характеристики распределения и оценить нормальность распределения.

Основы математического моделирования дорожного движения

Для оценки природы и характеристик транспортных потоков могут показаться полезными непосредственные наблюдения за транспортными потоками в условиях, когда дорожные контроллеры реализуют различные алгоритмы управления. Однако этот метод практически не осуществим, так как, во-первых, трудно найти подходящие транспортные потоки; во-вторых, это принципиально недопустимо, так как случайное экспериментирование на реальном объекте может привести к транспортным заторам и даже к ДТП. Следовательно, мы нуждаемся в модели действующей транспортной системы. Такая модель может иметь большое значение при проектировании систем управления дорожным движением. Другими словами созданная модель должна представлять реалистичную картину транспортного потока и быть доступной для систематического анализа. Затем необходимо найти эффективные концепции управления дорожным движением и получить возможность предсказывать поведение и характеристики управляемого движения.

Моделирование дорожного движения встречает ряд дополнительных трудностей, связанных сложностью сети дорог и случайным поведением водителей. Бессмысленно создавать модель, которая точно представляет все детали системы, поскольку это приводит к усложнению процесса ее проектирования. Поэтому при моделировании всегда используется ряд апроксемации реальных свойств системы. Хорошая модель, если такая существует, должна быть одновременно и точной и простой. Однако такие модели трудно создать в случае большой и сложной системы. Поэтому при исследовании характеристик системы в целом используют грубые модели, где ряд деталей опускается.

Моделирование – это средства (способ) изучения заданной системы путем ее замены более удобной для экспериментального исследования другой системой (моделью), сохраняющей существенные черты оригинала и позволяющей производить испытания моделей методом проб.

При изучении любого процесса методом моделирования в первую очередь необходимо построить математическое описание или математическую модель изучаемого процесса и определить величины, характеризующие процесс с количественной точки зрения.

Математическая модель – это результат формализации процесса, то есть построение четкого формального (математического) описания с необходимой степенью приближения к действительности. Математические модели представляются в форме уравнений. Недостатком такого метода является необходимость вводить грубые аппроксимации с целью нахождения приемлемого решения.

Нематематические методы включают как аналоговые модели, в которых используются специальные моделирующие устройства, представляющие реальную систему набором аналоговых электротехнических характеристик, так и цифровые имитационные модели на ЭВМ, в которых система моделируется с помощью программного обеспечения.

Подобные нематематические модели при правильном построении дают более точное представление объекта с меньшими аппроксимациями, чем математические модели, но требуют больших затрат на их создание, а также обеспечивают меньшую степень глубины исследования и прогноза поведения системы при серьезных изменениях в исходных концепциях. Следовательно, для получения характеристик всей системы в целом желательно использовать в качестве первого приближения математическую модель, а для детального уточнения характеристик элементов системы использовать нематематические методы.

Транспортный поток, движущейся по дорожной сети, состоит из множества автомобилей, которые управляются по более или менее свободному желанию водителей и маневры каждого автомобиля могут быть расценены как вероятностные события.

Недетерминированной (вероятностной, стохастической) является такая модель, в которой функционирование отдельных элементов или входные значения зависят от случайных параметров, т.е. описываются законами распределения случайных величин. Результат функционирования такой модели может быть предсказан только в вероятностном смысле, т.е. представляет собой среднее значение (математическое ожидание) или закон распределения.

Если обсуждаются условия, влияющие на безопасность движения на дороге или стартовые характеристики автомобилей, начинающих движение от регулируемого перекрестка, необходимо занимать вероятностную позицию и использовать, так называемые микроскопические модели, которые представляют движение отдельных автомобилей. Однако в случаях, часто наблюдаемых в большом городе или на скоростной дороге, когда много автомобилей движутся в группе (порционно), транспортный поток может быть рассмотрен как детерминированный и непрерывный (макроскопические модели).

Детерминированная модель – аналогическое представление закономерностей системы, при котором для заданного множества входных значений может быть получен на выходе только один единственный результат. Например, скорость движения автомобиля на заданном участке продольного профиля автодороги может быть определена в результате решений дифференциальных уравнений движения автомобиля. Тогда детерминированной моделью являются дифференциальные уравнения.

Модель или совокупность моделей, описывающих явление или систему в целом, вместе со средствами анализа их поведения образуют имитационную моделирующую систему. Примером имитационной системы, позволяющим определить основные регулирующие показатели движения автомобиля, может служить комплекс, состоящий из уравнений, которые описывают процесс движения автомобиля и дорожные условия.

Моделирование на ЭВМ – это разновидность математического моделирования. Оно имеет по сравнению с другими методами исследования известные преимущества: универсальность, гибкость, экономичность. Это позволяет в значительной мере решить одну из основных проблем современной науки и техники – проблему сложности.

Преимущества метода моделирования на ЭВМ:

1). Применение моделирования на этапах замысла и предварительного проектирования системы позволяет заранее определить успешность ее функционирования, что исключает непроизводительные затраты на построение нерациональных систем. Ответы на многие вопросы функционирования системы можно получить без дорогостоящего метода создания системы и ее апробации.

2). При помощи моделирования можно исследовать особенности функционирования системы в различных условиях. При этом параметры системы и окружающей среды можно варьировать для воспроизведения любой обстановки, в том числе и нереализуемой в натурных экспериментах.

3). Применение ЭВМ для моделирования, которое нельзя осуществить с помощью лабораторных и натурных экспериментов или аналитических методов часто является единственным реализуемым способом решения задачи. При этом продолжительность испытаний системы на моделе сокращается до минут, а на реальном объекте составляет дни месяцы.

4). С помощью метода моделирования необходимая информация, отражающая реальные условия, может быть быстро и в нужных количествах получена искусственным путем с учетом вероятностной природы ее элементов. Это достигается широко распространенными различными видами моделирования, в том числе методом статистического моделирования реализуемого на ЭВМ.

Классификация математических моделей транспортного потока

Пропускная способность автодорог и улиц и их пересечений является важнейшим критерием, который характеризует функционирование и эксплутационное состояние путей сообщения.

Изучение и обоснование этой характеристики явились первостепенными задачами, послужившими развитию моделирования транспортных потоков. Основы математического моделирования закономерностей дорожного движения были заложены в 1912г. профессором Г. Д. Дубелиром. Первая попытка обобщить математические исследования транспортных потоков в виде самостоятельного раздела прикладной математики, была сделана в 1963 г.Ф.Хейтом. Дальнейшие исследования и разработки в этой области нашли отражение в работах многих зарубежных и отечественных ученых. Нашедшие практическое применение в ОДД математические модели разделяются на две группы - детерминированные и вероятностные.

Детерминированные модели (ДМ).

Простейшей математической моделью описывающей поток автомобилей является»упрощённая динамическая модель». Её применяют для определения максимально возможной интенсивности движения по одной полосе дороги, при известной скорости потока

где А – кэфициэнт размерности;

динамический габарит; При выражении скорости км/ч, а в метрах приведенная формула является выражением для определения пропускной способности полосы:

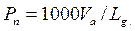
Данная динамическая модель составлена на основании двух упрощающих допущений:

1).скорость всех транспортных единиц в потоке одинакова;

2).транспортные средства однотипны (имеют одинаковые динамические габариты).

Динамический габарит автомобиля определяется длинной T.G плюс дистанция безопасности и плюс зазор до остановившегося впереди автомобиля (1-3 м):

Существует три принимаемых разными авторами подхода и определению динамического габарита:

1).При расчёте минимальной теоретической дистанции исходят из абсолютно равных тормозных свойств пары автомобилей и учитывают только время реакции ведомого водителя: .

Тогда учение: приобретает линейный характер. В этом случае возможная интенсивность транспортного потока не имеет приделы по мере увеличения скорости, одного это не соответствует реальным характеристикам потока и приводит к завышению возможной интенсивности.

2).При расчете на «полную безопасность» исходит из того, что дистанция d должна быть равна полному остановочному пути заднего автомобиля. Тогда динамический габарит:

.

В этой упрощённой формуле не выделен отрезок проходимый за время нарастания замедления, а учитывается только установившееся замедление ja. В этом случае уравнение приобретает вид квадратичной функции, а интенсивность имеет предел при определённом значении скорости.

3).Наиболее реальный подход, основанный на той предпосылке, что при расчёте дистанции безопасности d необходимо учитывать разницу тормозных путей или замедлений автомобилей, а так же то обстоятельство, что «лидер» в процессе торможения так же перемещается на расстояние равное своему тормозному пути. Тогда дистанция безопасности будет равна,

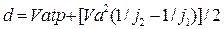
Если принять время реакции водителя tp=1с, а разность максимальных замедлений на сухом асфальте при экстренном торможении однотипных легковых автомобилей с учётом эксплутационного состояния тормозной системы в допустимых нормативами пределах около 2м/с , то динамический габарит выразится формулой:

Изложенный метод приемлем для ограниченных по составу и скорости транспортного потока условий, расчёт пропускной способности с учётом последнего выражения для непрерывного потока типичных легковых автомобилей даёт расчётное значение пропускной способности потока Рп:

при скорости .

Безопасность движения в такой плотной колонне с точки зрения психологического состояния водителя может быть обеспечена лишь при ограниченных скоростях движения выше 80км/ч время реакции водителя может достичь 2с, кроме того, из-за несовершенства тормозных систем автомобилей даже на дорогах с высоким коэфициэнтом сцепления при экстренном торможении автомобилей не гарантированно сохранение их устойчивого прямолинейного движения. Поэтому третий подход может быть рекомендован для скоростей не выше 80км/ч.

В зависимости от подхода к изучению характеристик дорожного движения совокупность разработанных математических моделей делится на макро и микро модели транспортных потоков. В результате изучения транспортных потоков высокой плотности и специальных экспериментов была предложена теория, следования за лидером: математическим выражением которой является микроскопическая модель транспортного потока.

Микроскопической её называют потому, что она рассматривает элемент потока – пару следующих друг за другом ТС. Особенностью этой модели является то, что в ней отражены закономерности комплекса ВАДС. В частности психофизиологический аспект управления автомобилей. Он заключается в том, что при движении в плотном транспортном потоке действия водителя обусловлены изменениями скорости лидирующего автомобиля и дистанции до него.

Экспериментальная проверка основного уравнения осуществлялась методом натурного имитационного моделирования. Дистанцию между автомобилями определяли киносъемкой или специальной амортизирующей лебедкой. Однако такой эксперимент уже в своей постановке содержит некоторую искусственность, искажающую реальный процесс (специальный подбор водителей, определенный режим движения и т.д.). Дорожные условия и общая транспортная ситуация рассматриваются в данной модели не в качестве отдельных параметров, а как проявляющиеся в значении скорости движения. Уравнения теории следования за лидером описывает взаимодействие между автомобилями с учетом реакции водителя на изменения в транспортном потоке, называемые стимулами.

Координаты скорости:

Ускорения: .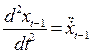

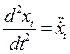Реакция на определенный стимул равна ускорению или замедлению движения ведомого автомобиля. Стимул принимается равным разности скоростей автомобилей:

«Чувствительность» - обратно пропорциональна дистанции между автомобилями и выражается при помощи коэффициента пропорциональности – а:

С учетом неизбежного запаздывания реакции водителя в соответствии с принятыми обозначениями можно записать уравнение теории следования за лидером:

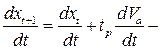основное уравнение теории следования за лидером.

В результате микроскопического подхода разработана динамическая модель движения плотного потока автомобилей, описывающая динамический габарит. Развитие этой модели привело к более сложной динамической теории следования за лидером, которая описывает процесс движения группы автомобилей при изменении скорости движения лидера. Взаимное расположение лидера и ведомого автомобиля можно выразить зависимостью:

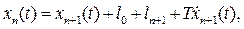
где расстояние между автомобилями в условиях затора, длина ведомого автомобиля, постоянная пропорциональности, имеющая размерность времени и характеризующая чувствительность.

Дифференцируя уравнение по времени, получим:

Откуда следует:

- уравнение первого основного закона для группы автомобилей теории «следования за лидером».

Ускорение ведомого автомобиля в любой момент времени прямо пропорционально разности скоростей ведущего и ведомого автомобилей. Принимая величину Т пропорциональной расстоянию между автомобилями d (T≈d), можем записать:

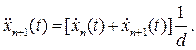
В таком виде мы получаем второе основное уравнение теории «следования за лидером». Ускорение ведомого автомобиля в любой момент времени Т прямо пропорционально разности скоростей ведущего и ведомого автомобилей и обратно пропорционально расстоянию между ними.

Г. И. Клинковштейн предложил уравнение теории следования за лидером в таком виде:

где а – константа пропорциональности, имеющая размерность скорости, 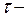запаздывание реакции водителя, 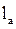- длина расчетного автомобиля.

В результате наблюдений установлены значения коэффициента пропорциональности а для различных типов автомобилей:

- для легковых среднего класса а=7,7; для грузовых автомобилей средней грузоподъемности а=6,4; для городских автобусов а=5,9; для автопоездов и троллейбусов а=4,4.

Приведенные динамические модели построены в предположении, что обгоны отсутствуют. В результате макроскопического подхода устанавливаются зависимости между основными характеристиками транспортного потока: интенсивностью, плотностью и скоростью. Основой для вывода таких зависимостей являются экспериментальные данные, анализ граничных условий, физические аналоги. При макромоделировании допускают, что движение однородно и допускают и исследуют средние характеристики транспортного потока.

Примером макромодели транспортного потока является уравнение состояния потока автомобилей:

На основании экспериментальных данных в 1934 году появилась первая модель Гриншилдса для однорядного потока. Она выражает зависимость между скоростью и плотностью транспортного потока. Лежащая в ее основе гипотеза гласит: когда плотность (степень насыщения дороги автомобилями) растет, водители снижают скорость для обеспечения безопасной дистанции, что математически записывается выражением:

или - модель Гриншилдса.

Гриншилдсом было установлено, что максимальная пропускная способность имеет место при:

, .

Эта модель предполагает линейную зависимость между скоростью и плотностью потока. Экспериментальные наблюдения показали, что эта зависимость нелинейна. Другие модели учитывают криволинейный характер зависимости в диапазонах малых и высоких плотностей потока. Д. Дрю предложил математическую модель ТП в предположении, что уравнение состояния дифференцируется по плотности:

При q=q₀, получаем .

или , , .

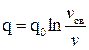Можно построить модель, в которой уравнение Гриншилдса является частным случаем. В общем случае, когда плотность повышается, водители снижают скорость и наоборот. Тогда:

, при п=-1,

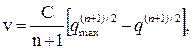при п не равном 1,

, при п=1.

Такая модель впервые была получена Гринбергом и лучше воспроизводит экспериментальную зависимость между скоростью и плотностью.

Модель Лайтхилла-Уизема позволила перейти от статистических функциональных зависимостей параметров транспортного потока к описанию их динамической связи по времени и координате. Этот переход был достигнут фактически формальным применением гидродинамического формализма. Таким образом, транспортный поток в их модели был представлен как непрерывный с плотностью , равной числу машин на единицу длины и расходом , равным числу машин, пересекающих черту за единицу времени. Тогда скорость потока равна:

,

то есть средняя скорость является детерминированной функцией плотности .

На участке дороги без съездов – въездов количество машин сохраняется:

.

Данное уравнение можно обобщить и на участок дороги с пересечениями:

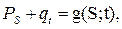
где обозначает скорость притока/оттока автомобилей.

Два последних уравнения образуют полную систему. Произведя подстановку получим:

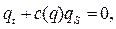
где 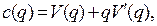скорость распространения возмущений.

Ударные Волны в транспортном потоке.

Рассмотрим модель Гриншилдса. Пусть скорость V лежит в пределах 0<V<V₀. Если по какой-либо причине скорость некоторой части потока снизится на , то интенсивность движения понизится на 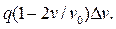Плотность этой части потока повысится и скорость будет далее снижаться. Возмущение скорости является незатухающим, что демонстрирует неустойчивость поведения ТП. В этом случае автомобили вынуждены неоднократно трогаться с места и останавливаться. Это явление носит название ударной волны.

На основании принципа неразрывности потока, как сплошной среды, получено выражение для вычисления скорости ударной волны:

Скорость движения ударной волны определяется тангенсом угла наклона прямой, которая соединяет две заданные точки основной диаграммы транспортного потока tgß и равен скорости ударной волны: tgß= .

К макромоделям также относят модели гидродинамической теории. Наиболее известны две из них, основанные на использовании аналогии в поведении транспортного потока и потока жидкости. Первая основана на уравнении неразрывности, которое обуславливает постоянство количества жидкости при ее протекании по водостоку и имеет вид в обозначениях принятых для транспортного потока:

В результате преобразований и упрощений имеем:

Вторая гидродинамическая модель использует известное из гидравлики понятие о потенциале давления жидкости и предполагает, что движение автомобиля выражается в виде функции некоторого «потенциала давления», зависящего от дорожных условий и психофизиологического состояния водителя с учетом согласования скорости со скоростью окружающих автомобилей в потоке.

Принципиальный подход к описанию транспортной модели.

Сложность задачи оптимизации транспортной системы в том, что, прежде всего, необходимо решить вопросы организации, обработки и анализа огромных массивов информации, а также в выборе математической модели в достаточной степени полно и точно имитирующей реальную динамику транспортной системы района, города или региона. Необходимость многогранного статистического исследования информации в области транспорта, а также алгоритмизация принципов обработки данных требует генерацию банка данных, как основы информационной модели.

Информационный уровень банка данных позволяет выполнить центральную задачу информационной модели – многоцелевое информационное обеспечение задач транспортной тематики.

При решении задачи исследования и минимизации количества ДТП содержание банка данных должно включать следующие массивы:

- массив документов о ДТП, описывающий происшествия одного или нескольких регионов (местоположение ДТП, время, тип, причины и т.д.);

- массив о состоянии транспортной инфраструктуры региона (геометрические элементы дороги, параметры транспортных потоков, дорожные знаки и т.д.).

Наряду с исследованиями в традиционных направлениях в области транспорта в последнее время интенсивно используются имитационные методы, позволяющие решать более широкий круг проблем, а также учитывать большое количество факторов, влияющих на поведение изучаемой системы.

Рассмотрим один из вариантов построения модели транспортной сети. Реальная система представляет собой функционирующую сеть перегонов и транспортных пересечений. Обычно сложность моделируемых систем обуславливает расчленение их на ряд подсистем. Выделим две подсистемы: перекрестки и перегоны, каждая из которых рассматривается иерархически с позиции едущего автомобиля и движения очереди в целом.

Рассматривая ij-перегон подразумеваем, что это перегон между i-тым и j-тым перекрестком. Рассматривать можно в общем случае ijkl-ный автомобиль (k-номер автомобиля, l-номер полосы). Аналогично расшифровывается индексация очередей.

Рассмотрим модель подсистемы перегон. В каждый момент времени t каждый ijkl-ный автомобиль может быть описан набором характеристик:

Т_ijkl(t) – тип автомобиля; N_ijkl(t) – номер автомобиля от начала вхождения в охватываемый моделью микрорайон и до выхода из него; С_ijkl(t) – расстояние от автомобиля до следующего перекрестка; V_ijkl(t) – cкорость автомобиля; А_ijkl(t) – ускорение или замедление автомобиля; D_ijkl(t) – случайная величина, характеризующая направление дальнего маршрута автомобиля при выходе с перегона; В_ijkl(t) – промежуточная величина, характеризующая одно из следующих качественных состояний:

1) автомобиль на входе;

2) ускорение;

3) желаемая скорость;

4) скорость менее желаемой;

5) замедление;

6) блокировка светофором;

7) блокировка лидером;

8) блокировка ДТП;

9) переход на другую полосу;

10) конец перегона.

В каждый момент t каждая ijl – ная очередь может быть описана набором характеристик:

N_ijl(t) – счетчик очереди; Ф_ijl(t) – фаза светофора, принимает значения (0;1); Ω_ijl(t) – остаточное время до поступления очередного автомобиля на перегон; τ_ijl(t) – остаточное время до смены фазы светофоров; τ¹_ijl(t) – остаточное время до момента ДТП; С_ijl(t) – расстояние от лидера очереди до последующего перекрестка; V_ijl(t) – скорость очереди; А_ijl(t) – ускорение очереди; М_ijl(t) – счетчик лидеров, покинувших перегон; В_ijl(t) – промежуточная величина, характеризующая качественное состояние ijl – ной очереди:

1) равномерное продвижение очереди;

2) ускорение;

3) замедление;

4) блокировка по фазе светофора;

5) блокировка по ДТП;

6) состояние отсутствия машин на полосе;

7) перестроение очереди на другую полосу;

8) растягивание очереди.

Рассмотрим состояние двух автомобилей: В_ijkl(t) – состояние первого автомобиля; В_ij(k-1)l(t) – состояние второго автомобиля (лидер).

Для первого автомобиля расстояние до последующего перекрестка: С_ijkl(t), а для второго - С_ij(k-1)l(t). Автомобиль лидер находится ближе к перекрестку, значит: С_ijkl(t)< С_ij(k-1)l(t). Если скорость очереди постоянна V_ijkl(t)= V_ij(k-1)l(t)= V_ijl(t), то время следования до последующего перекрестка тоже неодинаково: С_ijkl(t)/V_ijl(t)>С_ij(k-1)l(t)/V_ijl(t). Если выполняется условие: τ_ijl(t)> С_ijkl(t)/V_ijl(t)>С_ij(k-1)l(t)/V_ijl(t), то это означает, что ijkl–ный автомобиль в момент времени t движется с желаемой скоростью, имеет лидера, порядковый номер его не изменится в промежуток времени {t;t+1}, то есть смены лидеров не произойдет, автомобиль будет продолжать равномерное движение и перекресток будет пройден без остановки.

Стохастические модели.

Стохастические модели применяются для решения некоторых задач ОДД, когда необходимо располагать стохастическими характеристиками параметров транспортных потоков (н/п в зоне перекрестка). Исследованиями установлено, что для описания потоков сравнительно малой интенсивности, характеризующих вероятность проезда определенного числа ТС через сечение дороги применимо распределение Пуассона:

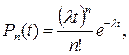
где вероятность проезда п–го числа автомобилей за время t; λ – основной параметр распределения (интенсивность авт/с); t – длительность отрезков наблюдения в с.; n – число автомобилей.

Практически для целей управления движением более необходимо располагать данными о характере распределения временных интервалов между следующими друг за другом ТС.

Если появление автомобилей характеризуется распределением Пуассона, то интервалы между автомобилями распределены по экспоненциальному закону:

где плотность распределения.

В транспортном потоке физически невозможно появление интервалов меньших, чем соответствующие длине типичного транспортного средства, поэтому более точным будет применение смещенного экспоненциального закона:

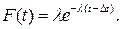
Упомянутые модели дают удовлетворительную сходимость с натуральными наблюдениями для однородных потоков, главным образом состоящих из легковых автомобилей. При смешанном потоке, а также воздействии некоторых внешних факторов может быть применено γ-распределение Эрланга (распределение к-го порядка):

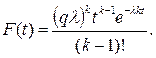
Движущиеся автомобили в общем случае разделяются на свободнодвижущиеся и следующие за лидером. Свободнодвижущиеся автомобили не имеют препятствия со стороны других участников движения и распределение интервалов времени для них может быть принято по экспоненциальному закону:

где φ – доля свободнодвижущихся автомобилей.

Движение ТС по дорогам в потоке большой интенсивности и, особенно, в зоне пересечений может быть рассмотрено на основании теории массового обслуживания. Задачи, решаемые с помощью этой теории, обычно сводятся к определению максимального числа «заявок», а также определению очереди в системе по истечении определенного промежутка времени. Применительно к транспортной задаче это означает возможность определения пропускной способности пересечения, задержек автомобилей и возникающих перед перекрестком очередей. Под «заявкой» понимают появление в сечении дороги одного транспортного средства.

Модель процесса обгона на двухполосной проезжей части

Моделирование производится в предположении, что появление автомобилей в заданном интервале τ подчинено закону распределения Пуассона. Время обгона определится как: ,

где динамические габариты автомобилей А и Б; 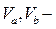скорости автомобилей А и Б.

Обгон быстроходным автомобилем А тихоходного автомобиля Б возможен, если выполнены следующие два условия:

- возникла необходимость обгона (перед автомобилем А в интервале времени τ появился хотя бы один тихоходный автомобиль Б);

- на встречной полосе в соответствующем временном интервале τ нет ни одного автомобиля.

Полное отсутствие автомобилей на встречной полосе при обгоне автомобилем А тихохдного автомобиля В возможно, если на встречной полосе не появится ни один автомобиль в интервале времени 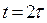. Вероятность отсутствия автомобиля на встречной полосе в интервале времени t равна:

,

где 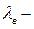основной параметр распределения (интенсивность движения по встречной полосе).

Эта формула определяет вероятность обгона сходу, т.е. без какого-либо следования за тихоходным автомобилем В. Если же на встречной полосе во временном интервале t находится автомобиль, то маневр обгона невозможен. Поскольку обгон сходу на двух полосных дорогах чаще невозможен рассмотрим процесс обгона со следованием за тихоходным автомобилем.

Модель строится следующим образом: все время следования разбивается на временные интервалы 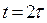. Если время следования меньше t, то данная модель не описывает процесс возможности обгона.

За время следования на встречной полосе во временном интервале t, начинающемся с момента окончания следования могут быть следующие явления:

- отсутствие автомобилей с вероятностью ;

- присутствие одного автомобиля с вероятностью ;

- присутствие двух автомобилей с вероятностью ;

- присутствие n автомобилей с вероятностью .

Вероятность того, что на встречной полосе присутствует хотя бы один автомобиль может быть представлена в следующем виде:

Вероятность возможности обгона со следованием в течение времени t включает в себя вероятность таких событий:

- вероятность того, что за время следования t на участке 1-2 (рис) отсутствуют автомобили ;

- вероятность того, что на участке 1-2 находится хотя бы один автомобиль, но к моменту прибытия автомобиля А в сечение 1-1 они успели освободить участок 1-2, необходимый для совершения маневра

Такая вероятность определяется зависимостью:

Тогда вероятность возможности обгона со следованием в течение времени t запишется:

вероятность обгона со следованием 1-го автомобиля; вероятность невозможности обгона.

Для того, чтобы обгон стал возможен по истечении времени 2t необходимо, чтобы встречная полоса на участке 2-3 к моменту прибытия автомобиля А в сечение 2-2 была свободна от автомобилей. Вероятность такого события выражается формулой:

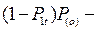вероятность, что полоса свободная.

Таким образом, вероятность возможности обгона после следования в течение времени 2t складывается из вероятности обгона по истечении времени t и вероятности возможности обгона по истечении времени 2t на участке 2-3:

После преобразований получим:

Аналогично определяется вероятность возможности обгона со следованием в течение времени 3t, 4t и т.д.

Тогда вероятность возможности обгона со следованием в течение времени nt определится по формуле:

Реализовать маневр обгона можно в том случае, если одновременно возникает необходимость в обгоне и возможность обгона. Выше рассмотрена вероятность возможности обгона. Вероятность необходимости обгона определяется появлением в прямом направлении хотя бы одного тихоходного автомобиля. Вероятность появления хотя бы одного автомобиля вообще определяется по распределению Пуассона:

где 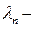интенсивность движения в прямом направлении.

Вероятность появления тихоходного автомобиля определяется содержанием таких автомобилей в потоке:

где 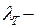интенсивность тихоходных автомобилей.

Таким образом, вероятность обгона одного автомобиля определится по формуле:

.

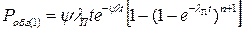В случае определения вероятности обгона пачки автомобилей, время обгона и вероятность обгона преобразуются к следующему виду:

.

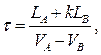
При математическом моделировании транспортных потоков особое внимание должно быть уделено выбору зависимостей, описывающих распределение случайных величин (явлений). В случае дискретных распределений используются биномиальные, отрицательные биномиальные, распределения Бернулли и т.д. Однако наиболее широко используется распределение Пуассона. К числу широко используемых непрерывных распределений относятся нормальное, распределение Вейбулла, Пирсона, показательное и т.д. Использование каждого из них должно быть тщательно обосновано. В ряде случаев сопоставление теоретических и фактических распределений позволяет ввести в известные зависимости поправочные коэффициенты.

Задача.

Элементы теории массового обслуживания

Одним из разделов теории вероятности, получившим большое развитие и практическое применение является теория массового обслуживания. Она направлена на решение задач организации и планирования процессов, в которых с одной стороны постоянно в случайные (или неслучайные) промежутки времени возникает заявка выполнения каких-либо работ, услуг, условий и т.д., а с другой происходит постоянное удовлетворение этих заявок, т.е. их выполнение.

Объектом изучения теории массового обслуживания (ТМО) является ситуация, когда имеется необходимость в обслуживании большого количества однородных заявок, которое может быть обеспечено одним и тем же средством. Заявка – это запрос на удовлетворение какой-либо потребности со стороны различных объектов (н/п появление автомобиля в сечении дороги, накопление очереди на выполнение работ (мойка, ремонт)). Удовлетворение этой потребности называется обслуживанием.

Средства, которые осуществляют обслуживание, называются обслуживающими аппаратами. Совокупность однородных обслуживающих аппаратов называется обслуживающей системой.

Общая схема ТМО автомобилей.

В большинстве задач массового обслуживания входящий поток зависит не от воли человека, а от ряда случайных факторов, что также относится и к времени обслуживания. Поэтому эти величины обычно описываются с помощью вероятностных характеристик.

От воли человека зависит организация системы обслуживания: каким образом распределить поступающие заявки между обслуживающими аппаратами, какое количество этих аппаратов необходимо выделить и каким образом их сгруппировать.

Поиск по сайту: