Сітки. Потоки на сітках. Задача про максимальний потік

До колонізації країн Африки звичаї зазнали впливу християнства, мусульманства, але він не був всепоглинаючим, тому що ні християни, ні мусульмани не укріпили панування своєї релігії, норми-звичаї продовжували діяти, навіть незважаючи на те, що вони суперечили новій вірі. Водночас вплив християнства та

>>>640>>>

ісламу зберігся й дотепер і позначається на характері формування правових систем.

Ефіопія стала християнською країною на початку IV ст., інші країни Африки і Мадагаскар — у XIX ст. Серед жителів Африки ЗО % — християни. Початок поширення ісламу в Африці припадає на XI ст. Регіони його впливу — країни Західної Африки, лише пізніше (XIV—XV століття) він охопив Сомалі та береги Індійського океану. 35 % населення екваторіальної Африки — мусульмани. Наслідком християнізації та ісламізації звичаєвого права Африки і Мадагаскару стала втрата віри в надприродне, магічне існування норм-звичаїв як створених світопорядком. Звичай став сприйматися лише тоді, коли він освячувався релігією. Це було першим кроком на шляху поступової втрати стародавніх звичаїв, їх авторитету. Відбувалося обмеження сфери їх впливу.

Другий крок у витисненні звичаєвого права припадає на період колонізації африканських держав (XIX -- 50—60-ті роки XX ст.). Насаджуються норми і судова система європейського лрава — англійського, бельгійського, португальського, французького. Французьке право введене у французьких колоніях Африки та Мадагаскарі; бельгійське — у Конго; португальське — в Анголі і Мозамбіку; загальне англійське право — в англійських колоніях; романо-голландське, а пізніше англійське загальне право — у Південної Африці[33]. Без правових норм колонізатори не могли створити необхідну систему виробничих відносин, яка забезпечувала б приплив сировини, збут продукції і т. под. Звичаєве право не могло створити необхідної правової бази, тому право запозичувалося від Заходу. Це стосується насамперед торгового, акціонерного, патентного, морського, трудового[34] права. Стали застосовуватися іноземні кодекси — французький Кримі-

>>>641>>>

нальний кодекс (із 1946 р. у французькій Західній Африці та Мадагаскарі), англійський Кримінальний і Кримінально-процесуальні кодекси (в англійській Західній Африці).

Правові форми особливо широко використовувала Англія при проведенні колоніальної політики. Вона створювала колоніальну імперію в Африці значною мірою через поширення там дії своєї юрисдикції. У кожній окремій колонії функціонувала система колоніальних судів, якій були властиві свої відмітні риси. Проте в цілому вона мала однакову структуру для всієї британської Африки. Нижчою судовою інстанцією всюди були традиційні місцеві суди, збережені англійцями відповідно до політики «непрямого управління», яку вони проводили. Вищою інстанцією були суди магістратів — власне англійські суди, створені для застосування в колоніях англійського права. Верховні суди також формувалися англійськими суддями.

Увійшовши до загальної системи колоніальних судів, традиційні суди стали територіальними, тобто правосудця відправлялося в рамках адміністративно-територіальних одиниць. Це суперечило характеру застосовуваних ними звичаєво-правових норм, тобто норм общини, а не території. Обмежувалося і застосування в судах норм звичаєвого права. Норми, що суперечили «справедливості і моралі» загального права, відкидалися.

Значних змін зазнало регулювання земельних відносин звичаєвим правом. За аналогією з судами в Англії земельні ділянки розглядалися суддями як власність. Общинна земля підлягала конфіскації та продавалася на виконання рішення про сплату боргів окремим особам. У результаті цього відчужувана земля ставала приватною власністю.

У витисненні звичаєвого права найзначнішу роль відіграли традиційні місцеві суди, ніж верховні суди і суди магістратів. Саме місцеві суди були зобов'язані відправляти правосуддя на основі норм звичаєвого права[35]. Верховні суди і суди магістратів керувалися звичаєвим правом у цивільних і кримінальних справах лише тоді, коли їх сторонами були тубільці.

Отже, колоніальні суди змінили звичаєве африканське право в напрямку оформлення дуалістичної системи права:

• право, уведене метрополіями;

• звичаєве право.

Сітки. Потоки на сітках. Задача про максимальний потік.

Сітка – це кінцевий граф без циклів і петель, орієнтований в одному загальному напрямку від вершини І, яка є входом (витоком) графа, до вершини S, яка є виходом графа (мал.1).

Будемо вважати, що по ребрам (і,j), де і<j, зі входу I у вихід S направляється деяка речовина (вантаж, ресурс, інформація і т. п.).

Максимальна кількість τіj речовини, яка може пропустити за одиницю часу ребро (і,j), називається її пропускною здібністю. В загальному випадку τ ≠ τ . Якщо вершини k і l на сітці не з’єднані, то τkl =τlk=0. На мал.1 пропускні здібності ребер вказані в дужках: перше число – пропускна здібність у напрямку від вершини і до вершини j, друге –в протилежному напрямку.

Мал.1.

Пропускні здібності ребер сітки можна задати квадратною матрицею n-го порядку (n-число вершин сітки). Оскільки τ = 0, то головна діагональ матриці складається з нулів. В таб.1 показана матриця R пропусних здібностей сітки, що зображена на мал.1

Таб.1.

Кількість х речовини, що проходить через ребро (і,j) за одиницю часу, називається потоком по ребру (і,j). В теорії потоків припускається, що якщо з вершини і у вершину j направляється потік величиною х , то величина потоку із j у і дорівнює -х , тобто.

х =-х (1)

Приймається також, що х =0.

Сукупність Х={х } потоків по всім ребрам (і,j) сітки називають потоком по сітці або просто потоком.

Потік по кожному ребру не перевищує його пропускну здібність:

х τ (і,j= ) (2)

Кількість речовини, що протікає у вершину, дорівнює кількості речовини, що з неї витікає

(і ) (3)

Формуючи потік на сітці, необхідно враховувати властивості (1) - (3).

Приклад 1. З формувати будь-який потік на сітці, що зображена на мал.1. Записати отриманий потік в матричний шлях 1-2-4-5. Ребро (4,5) на цьому не дозволяє пропустити по ньому потік, потужність якого перевищує одиницю. По повному шляху 1-2-5 можна було б пропустити 2 од.

Таб2.

J і
	-2
3	-3
		-1
		-1	-3	-1

Однак по ребру (1,2) вже передбачений потік в 1 од. Враховуючи це, пропускаємо по шляху 1-2-5 додатково 1 од. Розглядаючи повний шлях 1-3-5, помічаємо, що по ньому можна пропустити 3од. (тут граничним є ребро (3,5)). Таким чином ми організували на сітці потік, потужність f якого можна підрахувати, сумуючи або потоки х по ребрам (І,j), що виходить з вершини 1): х12+х13=2+3=5, або потоки х по ребрам (і,s), що виходять в стік S (у нас у вершину 5): х25+ х35+ х45=1+3+1=5.Числа х 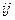створюють квадратну матрицю 5-го порядку, на головній діагоналі якої стоять нулі (х =0), а елементи,розміщені симетрично до головної діагоналі, рівні за абсолютною величиною і визначеннями побудована матриця отриманого потоку (табю2). Щоб відповісти на питання: чи буде цей потік максимальним, необхідно додаткове дослідження.

Із властивостей потоків по ребрам сітки випливає, що загальна кількість речовини, що виходить з витоку І, співпадає із загальною кількістю речовини, що поступає в стік S, тобто

f= (4)

Лінійну функцію (4) називають потужністю потоку на сітці. Виникає наступна задача лінійного програмування про максимальний потік: знайти сукупність Х={ } потоків по всім ребрам (і,j) сітки, яка задовольняє умовам (1)-(3) і максимізує функцію (4).

Щоб скласти алгоритми розв’язку цієї задачі, потрібні деякі важливі поняття. Нехай дана деяка сітка. Розділимо множину вершини цієї сітки на дві множини, що не перетинаються так, щоб виток І попав в підмножину Α, а в стік S –розріз, що відділяє витік І від стоку S. А саме: сукупність ребер (і,j), початкові вершини яких належать підмножині А, а кінцеві-підмножині В, називають розрізом сітки і позначають А/В. На мал.1 показаний розріз А/В, при якому вершини сітки опинились розбитими на підмножини А={1,2} і В={3,4,5}, а ребрами, що створюють розріз, сталі (1,3), (2,3), (2,4) і (2,5).

Якщо на сітці заданий деякий потік X={х }, то ребро (і,j) називають насиченим, якщо потік х по ньому співпадає з його пропускною здібністю τ (х = τ ), і ненасиченим, якщо потік менше пропускної здібності (х <τ ). Так на мал.1 ребро (1,2) насичене, як і ребра (4,5), (3,5), а всі інші ребра ненасичені.

Величина

R (А/В) = ,

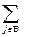
що являє собою суму пропускних здібностей τ всіх ребер розрізу, називається пропускною здібністю розрізу. Для розрізу на мал.1 R(А/В)=4+3+5+6=18.

Величина

Х(А/В)= ,

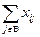що являє собою суму потоків х по всім ребрам розрізу, називається потоком через розріз. Для розрізу на мал.1 Х(А/В)=3+0+1+1=5.

В додатках важливе значення має теорема Форда-Фалкерсона: на будь-якій сітці максимальна величина потоку із витоку І в стік Ѕ дорівнює мінімальній пропускній здібності розрізу, що відділяє І від Ѕ.

Поиск по сайту: