 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задача про максимальний потік
Алгоритм побудови максимального потоку.
1. Побудувати деякий початковий потік Х  ={х
={х 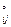 }.
}.
2. Організувати процедуру складання підмножини А вершин, що виходять з витоку І по ненасиченим ребрам. Якщо в цьому процесі стік S не попадає в підмножину А, то побудований потік максимальний і задача розв’язана. Якщо ж S попав у А, то перейти до п.3 алгоритму.
3. Виділити шлях із І в S, що складається з ненасичених ребер, і збільшити потік х  по кожному ребру цього шляху на Δ=min(τ
по кожному ребру цього шляху на Δ=min(τ  -
-  ), де мінімум береться по ребрам (і,j) вищезгаданого шляху. Тим самим буде побудований новий потік Х
), де мінімум береться по ребрам (і,j) вищезгаданого шляху. Тим самим буде побудований новий потік Х  ={х
={х  }. Після цього потрібно повернутися до п.2 алгоритму.
}. Після цього потрібно повернутися до п.2 алгоритму.
Приклад 2.  На сітці, що зображена на мал.2 з формувати потік максимальної потужності, направлений з витоку І в стік S, при умові, що пропускні здібності ребер в обох напрямках однакові. Виписати ребра, що становлять на сітці розріз мінімальної пропускної здібності.
На сітці, що зображена на мал.2 з формувати потік максимальної потужності, направлений з витоку І в стік S, при умові, що пропускні здібності ребер в обох напрямках однакові. Виписати ребра, що становлять на сітці розріз мінімальної пропускної здібності.
 |
Мал.2.
Розв’язання. У відповідності до п.1 алгоритму на сітці необхідно з формувати початковий потік Х  . Зробимо це наступним чином. По шляху 1-3-4-6 пропустимо 1од., по шляху 1-2-3-4-6-1од, по шляху 1-2-5-6-3од. В результаті потоки х
. Зробимо це наступним чином. По шляху 1-3-4-6 пропустимо 1од., по шляху 1-2-3-4-6-1од, по шляху 1-2-5-6-3од. В результаті потоки х  по ребрам сітки будуть дорівнювати: х
по ребрам сітки будуть дорівнювати: х  =4, х
=4, х 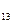 =1, х
=1, х  =1, х
=1, х 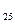 =3, х
=3, х 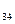 =2, х
=2, х 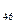 =2, х
=2, х 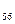 =3; потоки по іншим ребрам сітки дорівнюють нулю. Сукупність перерахованих потоків по ребрам і складе потік Х
=3; потоки по іншим ребрам сітки дорівнюють нулю. Сукупність перерахованих потоків по ребрам і складе потік Х  по сітці. Легко побачити, що умови (2) і (3), що накладаються на потоки по ребрам сітки, виконують. Матриця пропускних здібностей ребер даної сітки показана в табл.3, а матриця побудованого потоку – в табл.4.
по сітці. Легко побачити, що умови (2) і (3), що накладаються на потоки по ребрам сітки, виконують. Матриця пропускних здібностей ребер даної сітки показана в табл.3, а матриця побудованого потоку – в табл.4.
Табл.3.
| І j | ||||||
Табл.4.
| І j | ||||||
| -4 | ||||||
| -1 | -1 | |||||
| -2 | ||||||
| -3 | ||||||
| -2 | -3 |
Починаючи виконання п.2 алгоритму, складемо матрицю R-X  (талб.5), елементи τ
(талб.5), елементи τ  -х
-х  якої дозволяють судити про не насиченість ребер сітки. Насиченим ребрам будуть відповідати нульові елементи, а не насиченим – ненульові. Так, ребро (1,2) ненасичене, тому елемент τ
якої дозволяють судити про не насиченість ребер сітки. Насиченим ребрам будуть відповідати нульові елементи, а не насиченим – ненульові. Так, ребро (1,2) ненасичене, тому елемент τ  -х
-х 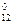 =6-4=2≠0, а ребро (2,5) насичене, тому τ
=6-4=2≠0, а ребро (2,5) насичене, тому τ 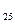 -х
-х 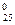 =3-3=0.
=3-3=0.
Знаючи матрицю R-X  , можна з формувати підмножину А вершин, в які можна попасти з витоку І, рухаючись тільки по ненасиченим шляхам (тобто виконати п.2
, можна з формувати підмножину А вершин, в які можна попасти з витоку І, рухаючись тільки по ненасиченим шляхам (тобто виконати п.2
Табл.5.
| і j | ||||||
алгоритму), а також виділити (якщо потік Х  не максимальний) ці шляхи і з їх допомогою збільшити потужність потоку (тобто виконати п.3 алгоритму).
не максимальний) ці шляхи і з їх допомогою збільшити потужність потоку (тобто виконати п.3 алгоритму). 
Вершини підмножини А виділяють поступово, починаючи з витоку І. З цією метою переглядають перший рядок матриці R-Х  (рядок І) і виписують номери і
(рядок І) і виписують номери і 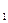 , і
, і 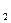 ,..., і
,..., і 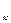 вершин, що відповідають ненульовим елементом рядка. Це і будуть вершини, в які можна попасти з витоку І, рухаючись по ненасиченим ребрам. Будимо записувати виявлені таким чином вершини у вигляді І║ і
вершин, що відповідають ненульовим елементом рядка. Це і будуть вершини, в які можна попасти з витоку І, рухаючись по ненасиченим ребрам. Будимо записувати виявлені таким чином вершини у вигляді І║ і 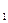 , і
, і 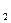 ... і
... і 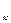 і називати подібний запис стиком вершини І. Далі розглядають кожну з вершин і
і називати подібний запис стиком вершини І. Далі розглядають кожну з вершин і 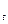 отриманого списку і складають для неї аналогічно свій список. При цьому вершини, що зустрічалися в попередніх списках, повторно не виписуються. Якщо в цьому процесі стік S не зустрінеться, - потік максимальний і задача розв’язана, якщо ж при складанні наступного стику в ньому з’явиться стік S, то потік не максимальний і його потужність можна збільшити.
отриманого списку і складають для неї аналогічно свій список. При цьому вершини, що зустрічалися в попередніх списках, повторно не виписуються. Якщо в цьому процесі стік S не зустрінеться, - потік максимальний і задача розв’язана, якщо ж при складанні наступного стику в ньому з’явиться стік S, то потік не максимальний і його потужність можна збільшити.
Повернемося до нашого прикладу. В даному випадку І = 1, S = 6. Побудуємо під множину А, послідовно складаючи списки вершин, починаючи з вершини 1. Дивлячись на перший рядок матриці R-X0(див. Табл. 5), у список вершини 1 попаде одна вершина 2, оскільки елемент другого стовпця цього рядка відмінний від нуля. Отже, запишемо: 1║ 2. Тепер переходимо до складання списку вершини 2 як вершини, що ввійшла в список вершини 1. В другому рядку матриці два елементи відмінні від нуля: 10 і 1. Але 10 відповідає вершині 1, яка вже присутня в підмножині А, тому повторно її в списки не включаємо. Елемент 1 відповідає вершині 3, вона зустрічається вперше, тому включаємо її в список вершини 2. Таким чином отримуємо наступний список: 2║ 3. Аналогічно отримуємо інші списки. В результаті маємо набір:
 |  |  |  |  |
1 ║ 2, 2║ 3, 3║ 4, 4║ 5, 5 ║ 6. (5)
Аналізуючи списки (5), помічаємо, що стік 6 попав у під множину А, оскільки опинився у списку однієї з вершин підмножини А (в даному випадку вершини 5). Це означає, що існує шлях з витоку І в стік S (у нас з 1 в 6), що складаються з ненасичених ребер.
Продовжимо деталізувати алгоритм, побудову ненасиченого шляху з І в S починають з останнього ребра цього шлях. Ним буде ребро (і n-1, S), де і n-1 – вершина, в список якої попав стік S. Далі виписують ребро (і n-2 і n-1), де і n-1 – вершина, в список якої попала вершина і 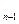 , і так до тих пір, доки на кроці не зустрінеться ребро (І, і,), яким і почнеться вихідний ненасичений шлях. Таким чином, ненасичений шлях з І в S міститься з ребер (І, і
, і так до тих пір, доки на кроці не зустрінеться ребро (І, і,), яким і почнеться вихідний ненасичений шлях. Таким чином, ненасичений шлях з І в S міститься з ребер (І, і 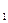 ), (і
), (і 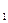 , і
, і 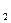 ),..., (і
),..., (і 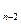 , і
, і 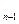 ), (і
), (і 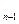 , S).
, S).
Повернемося до нашого прикладу. Переділяючись списки (S) з кінця до початку, помічаємо, що ребром (і 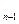 , S) в даному випадку є ребро (5,6), ребром (і
, S) в даному випадку є ребро (5,6), ребром (і 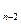 , і
, і 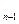 ) – ребро (4,5),..., і, нарешті, ребром (І, і
) – ребро (4,5),..., і, нарешті, ребром (І, і 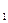 ) – ребро (1,2). Таким чином, шлях з витоку 1 у стік 6 по ненасиченим ребрам пройде через вершини 1,2,3,4,5 і 6.
) – ребро (1,2). Таким чином, шлях з витоку 1 у стік 6 по ненасиченим ребрам пройде через вершини 1,2,3,4,5 і 6.
Після виділення ненасиченого шляху з витоку І в стік S залишається за допомогою матриці R-Х  визначити величину ∆=min(
визначити величину ∆=min(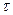
 -х
-х  ), на яку потрібно збільшити потік по кожному ребру (і,j) виділеного шляху, щоб отримати новий потік Х
), на яку потрібно збільшити потік по кожному ребру (і,j) виділеного шляху, щоб отримати новий потік Х  більшої потужності (на ∆ одиниць).
більшої потужності (на ∆ одиниць).
В нашому прикладі, як видно з таблиці 5, по ребру (1,2) додатково можна припустити 2 од., по ребрам (2,3), (3,4), (4,5) і (5,6) – відповідно 1, 1, 1 і 2 од., так, що збільшити потік по всьому шляху 1-2-3-4-5-6, що складається із вказаних ненасичених ребер, можна на величину
∆= 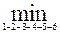 (2,1,1,1,2)=1
(2,1,1,1,2)=1
Для побудови матриці нового потоку Х  до відповідних елементів х
до відповідних елементів х 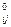 матриці Х
матриці Х 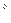 додається до n.2 алгоритму, і так до отримання максимального потоку.
додається до n.2 алгоритму, і так до отримання максимального потоку.
В розглядаємо му прикладі на величину ∆=1 збільшаться елементи х 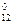 , х
, х 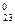 , х
, х  , х
, х  і х
і х 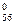 матриці Х
матриці Х  (див. Табл.. 4). З урахуванням (1) прийдемо до матриці нового потоку Х
(див. Табл.. 4). З урахуванням (1) прийдемо до матриці нового потоку Х  (табл. 6). Потужність цього потоку стала дорівнювати 5+1=2+4=6 од.
(табл. 6). Потужність цього потоку стала дорівнювати 5+1=2+4=6 од.
Побудований потік Х  знову потрібно дослідити на оптимальність, тобто повернутися до операцій n.2 алгоритму. З цією метою як і при досліджені потоку Х
знову потрібно дослідити на оптимальність, тобто повернутися до операцій n.2 алгоритму. З цією метою як і при досліджені потоку Х  , складаємо матрицю R-Х
, складаємо матрицю R-Х  (табл. 7), а по ній – списки
(табл. 7), а по ній – списки
Табл. 6
| і | ||||||
| -5 | ||||||
| -1 | -2 | |||||
| -3 | ||||||
| -3 | -1 | |||||
| -2 | -4 |
Табл. 7
| і | ||||||


вершин, що досягаються з витоку І по ненасиченим шляхом. В результаті отримуємо такі списки:
 |  |
1║2, 2║. (6)
Якщо видно зі списків (6), стік 6 не попав у список вершин, досягаються з І по ненасиченим ребрам. Це означає, що потік Х  максимальний. Залишається накласти його на сітку з указаним напрямку потоків по окремим ребрам (мал.3).
максимальний. Залишається накласти його на сітку з указаним напрямку потоків по окремим ребрам (мал.3).
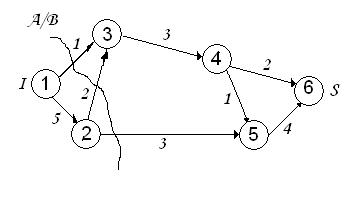
Мал.3.
Використовуючи списки (6), виділимо підмножини А і В, на які розбита множина всіх вершин: А={1,2},В={3,4,5,6}. А зараз випишемо ребра, що створюють розтин А/В мінімальної пропускної здібності: (1,3), (2,3), (2,5).
Розглянемо деякі додатки задачі про максимальний потік.
Поиск по сайту: