 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Транспортна задача за критерієм часу
Приклад 3. (транспортна задача за критерієм часу). В табл.8 вказані запаси а  деякого однорідного вантажу, що знаходиться у постачальників А
деякого однорідного вантажу, що знаходиться у постачальників А  (і=
(і= 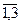 ).
).
Табл.8.
а   в в 
| |||
Цей вантаж необхідно доставити за мінімальний час отримати В 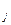 , потреби в
, потреби в 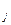 (j=
(j= 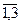 ) яких відомі. В таблиці наведений час t
) яких відомі. В таблиці наведений час t  доставки вантажу (незалежно від об’єму поставки) кожним постачальником А
доставки вантажу (незалежно від об’єму поставки) кожним постачальником А  кожному споживачу В
кожному споживачу В 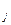 . Скласти план мінімальних витрат часу на переведення, при якому попит споживачів повністю задовольняється.
. Скласти план мінімальних витрат часу на переведення, при якому попит споживачів повністю задовольняється.
Розв’язання. Відразу ж відмітимо, що в нашому прикладі загальний запас вантажу дорівнює сумарному попиту, а тому потреби всіх отриманих вантажів можна задовольнити (закрита задача). У випадку відсутності вищезгаданої рівності (відкрита задача) попередньо вводять фіктивного постачальника (споживача) із запасом (попитом) вантажу, що дорівнює небалансу, і формально зводять задачу до закритої.
Щоб звести розв’язання розглядаємо задачі до задачі про максимальний потік, побудуємо сітку, в якій три вершини будуть відповідати постачальником А 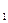 , А
, А 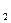 , А
, А  , три – споживачам В
, три – споживачам В 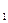 , В
, В 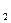 , В
, В  , одна – витоку I і одна – стоку S (мал.4).
, одна – витоку I і одна – стоку S (мал.4).
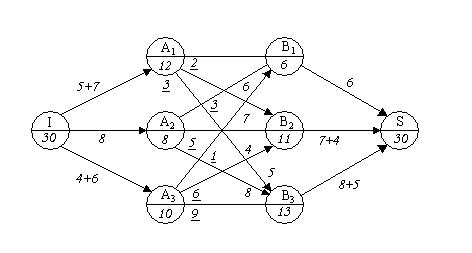 |
Пропускні здібності ребер нехай дорівнюють:
r  =а
=а  , r
, r  =0, r
=0, r  =b
=b 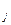 , r
, r  =0, r
=0, r 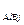 = r
= r  =∞. (7)
=∞. (7)
В ребрах (А  , В
, В 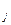 ) вкажемо терміни t
) вкажемо терміни t  доставки вантажу. Час доставки за маршрутами І-А
доставки вантажу. Час доставки за маршрутами І-А  і В-S нехай дорівнює нулю. Для зрозумілості на мал.4 пропускні здібності і деякі терміни не вказані, а терміни доставки по маршруту там (А
і В-S нехай дорівнює нулю. Для зрозумілості на мал.4 пропускні здібності і деякі терміни не вказані, а терміни доставки по маршруту там (А  В
В 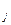 ) підкреслені знизу, щоб відрізнити їх від потоків х
) підкреслені знизу, щоб відрізнити їх від потоків х  по ребрам сітки.
по ребрам сітки.
Після побудови сітки виникає задача про максимальний потік потужністю 30 од. (сумарний запас вантажу, який слід пропустити по сітці), що проходить через сітку за мінімальний час.
У відповідності до алгоритму задачі про максимальний потік побудуємо на сітці початковий потік Х  . Оскільки мінімізувати потрібно час доставки вантажу, звичайно “завантажувати” в видно, що по ребру (А
. Оскільки мінімізувати потрібно час доставки вантажу, звичайно “завантажувати” в видно, що по ребру (А 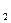 ,В
,В  ) час доставки. З мал.4 видно, що менший за інших, тому пропустимо по шляху І-А
) час доставки. З мал.4 видно, що менший за інших, тому пропустимо по шляху І-А 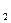 -В
-В  -S, що містить це ребро, наприклад 8 од. Наступним можна завантажити, наприклад, ребро (А
-S, що містить це ребро, наприклад 8 од. Наступним можна завантажити, наприклад, ребро (А 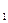 ,В
,В  ) з t
) з t 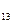 =3, пропустивши по шляху І-А
=3, пропустивши по шляху І-А 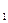 -В
-В  -S 5 од. Тим самим попит споживача В
-S 5 од. Тим самим попит споживача В  буде повністю задоволений. Дані доцільно завантажити 7 одиницями ребро (А
буде повністю задоволений. Дані доцільно завантажити 7 одиницями ребро (А 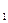 , В
, В 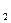 ) з t
) з t  =2 в результаті пропуску 7 од. по шляху І-А
=2 в результаті пропуску 7 од. по шляху І-А 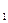 - В
- В 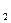 -S. При цьому буде повністю вичерпаний запас вантажу в пункті А
-S. При цьому буде повністю вичерпаний запас вантажу в пункті А 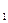 . Завершення процесу формування потоку Х
. Завершення процесу формування потоку Х  можна прослідкувати по мал.4. Це маршрути І-
можна прослідкувати по мал.4. Це маршрути І- 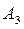 - В
- В 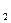 -S з 4 од. вантажу і І-
-S з 4 од. вантажу і І- 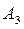 -
- 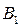 -S з 6 од. вантажу. Величини потоків по ребрах вказані поруч зі стрілками, що позначають напрямок цих потоків.
-S з 6 од. вантажу. Величини потоків по ребрах вказані поруч зі стрілками, що позначають напрямок цих потоків.
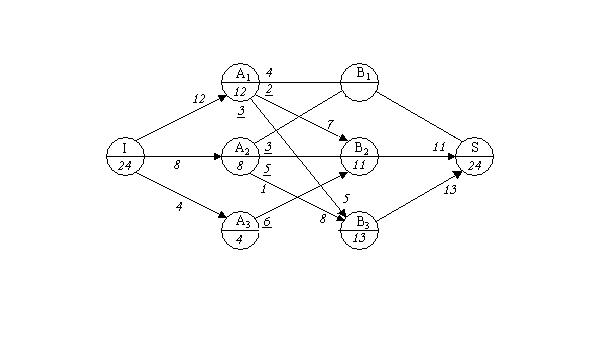 Аналізуючи побудований потік Х
Аналізуючи побудований потік Х  (потужністю в 30 од. часу), помічаємо, що час найбільш тривалого перевезення дорівнює 7 і відповідає маршруту
(потужністю в 30 од. часу), помічаємо, що час найбільш тривалого перевезення дорівнює 7 і відповідає маршруту 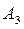 -
- 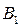 . Але в
. Але в 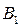 можна потрапити або з А
можна потрапити або з А 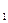 за 4 од. часу, або з А
за 4 од. часу, або з А 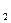 за 3 од. часу, тобто швидше, ніж з А
за 3 од. часу, тобто швидше, ніж з А  . Виникає припущення про те, що використання будь-якого з цих маршрутів дозволить замінити маршрут А
. Виникає припущення про те, що використання будь-якого з цих маршрутів дозволить замінити маршрут А  -В
-В 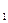 . Виключимо маршрут А
. Виключимо маршрут А  -В
-В 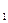 і маршрути, для яких t
і маршрути, для яких t  ≥7, зберігаючи розподіл потоків на ребрах, що залишилися таким, як і раніше. В нашому випадку, крім А
≥7, зберігаючи розподіл потоків на ребрах, що залишилися таким, як і раніше. В нашому випадку, крім А  -В
-В 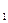 , доведеться виключити маршрут А
, доведеться виключити маршрут А  -В
-В  з t
з t 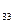 =9.
=9.
Мал.5.
Далі будуємо матриці R за правилами (7), Х  і R-Х
і R-Х  (табл.9-11).
(табл.9-11).
Табл.9.
| І | А 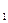
| А 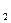 
| А3 | В1 | В2 | В3 | S | |
| І | ||||||||
А1   
| ∞ | ∞ | ∞ | |||||
А2 
| ∞ | ∞ | ∞ | |||||
| А3 | ∞ | |||||||
| В1 | ∞ | ∞ | ||||||
| В2 | ∞ | ∞ | ∞ | |||||
| В3 | ∞ | ∞ | ||||||
| S |
Табл.10.
| І | А1 | А2 | А3 | В1 | В2 | В3 | S | |
| І | ||||||||
| А1 | -12 | |||||||
| А2 | -8 | |||||||
| А3 | -4 | |||||||
| В1 | ||||||||
| В2 | -7 | -4 | ||||||
| В3 | -5 | -8 | ||||||
| S | -11 | -13 |
Табл.11.
| І | А1 | А2 | А3 | В1 | В2 | В3 | S | |
| І | ||||||||
| А1 | ∞ | ∞ | ∞ | |||||
| А2 | ∞ | ∞ | ∞ | |||||
| А3 | ∞ | |||||||
| В1 | ∞ | ∞ | ||||||
| В2 | ∞ | ∞ | ||||||
| В3 | ∞ | ∞ | ||||||
| S |
За табл.11 будуємо список вершин, що ведуть з І в S по ненасиченим ребрам:
 | |||||||||||
 |  |  |  |  | |||||||
І ║ А3, А3║ В2 В2║А1,А 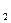 А1║В1,В3, А2║… В1║ S
А1║В1,В3, А2║… В1║ S
Оскільки стік S попав у список, то потужність потоку, дійсно, можна збільшити. Для визначення величини ∆ додаткового потоку по складеним спискам формується ланцюг ненасичених ребер: (І, А3), (А3, В2), (В2, А1), (А1, В1), (В1, S), що веде в стік S, і по ребрам цього ланцюга на основі табл.11 визначається ∆= min(6,∞, ∞, ∞, 6)=6.
Збільшуючи на 6 од. потоки по ребрах вказаного ланцюга (в табл.10), отримуємо новий потік Х 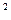 , матриця якого представлена в табл.12, а сітка, що містить цей потік, зображена на мал.6.
, матриця якого представлена в табл.12, а сітка, що містить цей потік, зображена на мал.6. 
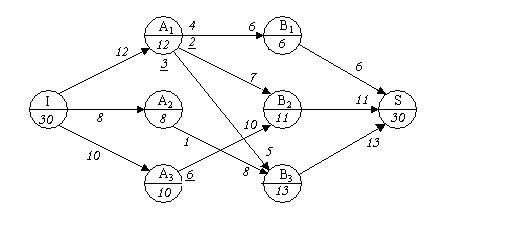 |
Табл.12.
| І | А1 | А2 | А3 | В1 | В2 | В3 | S | |
| І | ||||||||
| А1 | -12 | |||||||
| А2 | -8 | |||||||
| А3 | -10 | |||||||
| В1 | -6 | |||||||
| В2 | -1 | -10 | ||||||
| В3 | -5 | -8 | ||||||
| S | -6 | -11 | -13 |
Аналізуючи сітку на мал.6, помічаємо, що час найбільш тривалого переведення дорівнює 6 і відповідає маршруту А3-В2. Однак з вершини А3 немає можливості вивести вантаж за час, менший 6 од., відповідно, розподіл, що отримали на сітці, показаній на мал.,6 найкращий і задача розв’язання. Для більшої наявності відповідь можна записати у формі табл.13.
Табл.13
| В1 | В2 | В3 | |
| А 1 | |||
| А2 | - | - | |
| А3 | - | - |
Поиск по сайту: