 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Інтегруючи ланцюги
|
Читайте также: |
Інтегруючим називається електричний ланцюг, в якому вихідна величина пропорційна інтегралу від вхідної величини (мал. 1.14). Широке застосування на практиці одержав інтегруючий rC- ланцюг.
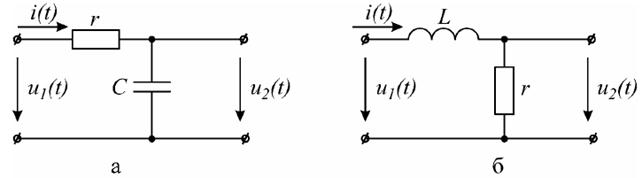
Рисунок 1.14 – Інтегруючи ланцюги
Напруга на виході ланцюга
Якщо напруга на конденсаторі складає малу частину від напруги на опорі, то струм i(t) в ланцюзі буде пропорційний вхідній напрузі:
отже,
Отже, при виконанні умови
uc << ur або u 1≈ ur
ланцюг rC є інтегруючим.
При не синусоїдальному сигналі умова повинна виконуватися для гармонійної складової найменшої частоти ω H, тобто частоти повторення вхідного сигналу. На практиці не обходжений виконати умову
Як приклад розглядається вихідна напруга інтегруючого rC-ланцюга при дії на вхід прямокутного імпульсу (рис. 1.15, а).
Рисунок 1.15 – Графік напруги реального ланцюга що інтегрує
Вихідна напруга на місткості в інтервалі часу від t 1 до t 2 змінюється згідно із законом
Максимальна напруга на виході
За умови, що постійна часу τ ланцюги більше тривалості вхідного імпульсу, вихідна напруга на ділянці 2 1 t t − змінюється майже по лінійному закону, тобто вихідна напруга є інтегралом вхідної напруги прямокутної форми.
Слід зазначити, що чим більше τ, тим точніше виконується операція інтеграції (закон лінійності), але вихідна напруга по величині значно менше за вхідну (рис. 1.15, в).
Час t u вих вимірюється на рівні 0,1 U m вих, як це показано на рис. 1.15, б.
3.4 Порядок виконання роботи
1. Запустити на комп'ютері програму Electronics Workbench.
2. Зібрати в програмі Electronics Workbench схему відповідно до рис.1.16.
Рисунок 1.16 – Схема для дослідження ланцюгів з реактивними елементами
Об’єктом дослідження є ланцюг, який утворюються із джерела напруги U, конденсатора С1, котушки індуктивності L1 та резисторів R1, R2. Перемикачі (ключі) К1, К2, К3 і К4 забезпечують комутацію схеми на той чи інший досліджуваний реактивний двополюсник і дають можливість організувати спостереження осцилограм і вимірювання струмів та напруги на різних ділянках ланцюга.
3. Підключити до досліджуваного ланцюга за допомогою ключа К1 генератор прямокутних імпульсів (зміна положення ключа здійснюється натисненням клавіші «G» на клавіатурі).
4. Для дослідження RC -ланцюга за допомогою ключа К2 (натисненням клавіші 1 на клавіатурі) під’єднується конденсатор С1. Ключ К3 встановлюється (натисненням клавіші I на клавіатурі) у положення, що забезпечує режим спостереження і вимірювання параметрів вхідного сигналу, який подається на ланцюг. Ключ К4 встановлюється у нижнє (за схемою) положення для забезпечення режимів спостереження і вимірювання параметрів струму ланцюга. Зміна положення ключа К4 здійснюється натисненням клавіші «О» на клавіатурі.
Включити схему за допомогою перемикача 
, або, натиснувши на клавіатурі Ctrl+G. Дочекатися появи зображення на екрані віртуального осцилографа і замалювати осцилограми вхідної напруги і струму конденсатора. Вимкнути схему, натиснувши на клавіатурі Ctrl+Т.
Визначити параметри змальованих сигналів (амплітуду, тривалість, період). За осцилограмами визначити тривалість перехідного процесу у досліджуваному ланцюзі і розрахувати постійну часу досліджуваного ланцюга. Приклад осцилограми (на екрані віртуального осцилографа) приведено на рис. 1.17.
Рис. 1.17 - Приклад осцилограми RC -ланцюга
5. Перевести ключ К4 у верхнє (за схемою) положення, що дає можливість спостерігати осцилограми напруги на конденсаторі С1 досліджуваного ланцюга.
Включити схему і, дочекавшись появи зображення на екрані віртуального осцилографа, замалювати осцилограми вхідної напруги і напруги на конденсаторі С1.
Визначити параметри змальованих сигналів (амплітуду, тривалість, період). За осцилограмами визначити тривалість перехідного процесу у досліджуваному ланцюзі і розрахувати постійну часу досліджуваного ланцюга. Приклад осцилограми приведено на рис. 1.18.
Рис. 1.18 - Приклад осцилограми напруги на конденсаторі С1
6. Для дослідження RL -ланцюга встановити ключ К2 у положення, що забезпечує це дослідження, а ключ К4 - у нижнє (за схемою) положення, яке забезпечує вимір струмів схеми.
Включити схему і, дочекавшись появи зображення на екрані віртуального осцилографа, замалювати осцилограми вхідної напруги і струму котушки.
Визначити параметри змальованих сигналів (амплітуду, тривалість, період). За осцилограмами визначити тривалість перехідного процесу у досліджуваному ланцюзі і розрахувати постійну часу досліджуваного ланцюга. Приклад осцилограми приведено на рис. 1.19.
Рис. 1.19 - Приклад осцилограми RL -ланцюга
7. Перевести ключ К4 у верхнє по схемі положення, що дає можливість спостерігати осцилограми напруги на котушці індуктивності L1 досліджуваного ланцюга.
Включити схему і, дочекавшись появи зображення на екрані віртуального осцилографа, замалювати осцилограми вхідної напруги і напруги котушки досліджуваного ланцюга. За осцилограмами визначити тривалість перехідного процесу у досліджуваному ланцюзі і розрахувати постійну часу досліджуваного ланцюга. Приклад осцилограми приведено на рис. 1.20.
Рис. 1.20 - Приклад осцилограми напруги на котушці індуктивності L1
3.5 Зміст звіту
До звіту заносять:
- тему та мету роботи;
- принципову схему електричного кола, яке аналізується;
- епюри струмів і напруги на окремих ділянках ланцюга досліджуваних схем;
- розрахунки тривалості перехідних процесів;
- висновки по роботі.
3.6 Контрольні питання
1. Які елементи ланцюгів називають реактивними?
2. Від яких параметрів ланцюга залежить швидкість зміни струму в ланцюги і напруги на окремих її ділянках?
3. Фізичне поняття тривалості часу перехідного процесу у ланцюзі з реактивними елементами.
4. Фізичне поняття «постійної часу ланцюга» з реактивними елементами.
5. Визначення постійної часу rL - ланцюга і вплив величини опору на тривалість перехідного процесу.
6. Визначення постійної часу ланцюга графічно і аналітично.
7. Диференціюючи ланцюги і фізичний сенс процесів, що відбуваються в них.
8. Інтегруючи ланцюги і фізичний сенс процесів, що відбуваються в них.
9. 5. Визначення постійної часу rС - ланцюга і вплив величини опору на тривалість перехідного процесу.
10. Визначити умову, при якій rC-ланцюг є диференціруючим.
11. Визначити умову, при якій rC-ланцюг є інтегруючим. Вибір r і С інтегруючого ланцюга.
12. сформулюйте закони комутації.
Лабораторна робота № 2
дослідження перехідних процесів в лінійних ланцюгах другого порядку
1.1 Мета роботи: експериментальне дослідження перехідного процесу в ланцюзі з послідовним з'єднанням RLC- елементів при включенні її в ланцюг постійного струму.
1.2 Зміст роботи: для заданого електричного кола (рис.2.1):
- встановити задані (за варіантами) параметри елементів;
- скласти характеристичне рівняння та знайти його коріння;
- по результатам рішення визначити вид перехідного процесу в досліджуваному ланцюзі;
- провести необхідні вимірювання величин струмів та напруги (табл. 2.2);
- зарисувати епюри струмів та напруги на елементах досліджуваного ланцюга;
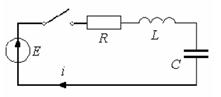
Рисунок 2.1 – Принципова електрична схема кола
1.3 Теоретичні відомості: аналізу перехідного процесу електричного кола другого порядку.
При всіх змінах в електричному ланцюзі: включенні, виключенні, короткому замиканні, коливаннях величини якого-небудь параметра і т.п. - в ній виникають перехідні процеси, які не можуть протікати миттєво, оскільки неможлива миттєва зміна енергії, яка запасена в електромагнітному полі ланцюга. Таким чином, перехідний процес обумовлений невідповідністю величини запасеної енергії в магнітному полі котушки і електричному полі конденсатора її значенню для нового стану ланцюга.
При перехідних процесах можуть виникати великі перенапруження, надструми, електромагнітні коливання, які можуть порушити роботу пристрою аж до виходу його з ладу. У інших випадках, перехідні процеси знаходять корисне практичне застосування (у різних електронних генераторах). Все це обумовлює необхідність вивчення методів аналізу нестаціонарних режимів роботи ланцюга.
Основні методи аналізу перехідних процесів в лінійних ланцюгах:
1. Класичний метод, що полягає в безпосередній інтеграції диференціальних рівнянь, які характеризують електромагнітний стан ланцюга.
2. Операторний метод, що полягає в рішенні системи рівнянь, алгебри, щодо зображень шуканих змінних з подальшим переходом від знайдених зображень до оригіналів.
3. Частотний метод, що заснований на перетворенні Фур'є і знаходить широке застосування при рішенні задач синтезу.
4. Метод розрахунку за допомогою інтеграла Дюамеля, використовуваний при складній формі кривої збуджуючої дії.
5. Метод змінних стану, що є впорядкованим способом визначення електромагнітного стану ланцюга на основі рішення системи диференційних рівнянь першого порядку, записаних в нормальній формі (формі Коші).
Оскільки короткий виклад всіх вище перелічених методів скрутно, нижче приведено короткий опис тільки класичного методу аналізу.
Поиск по сайту: