 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Класичний метод розрахунку
Класичний метод розрахунку перехідних процесів полягає в безпосередній інтеграції диференціальних рівнянь, які характеризують зміни струмів і напружень на ділянках ланцюга в перехідному процесі.
У загальному випадку при використанні класичного методу розрахунку складаються рівняння електромагнітного стану ланцюга по законах Ома і Кірхгофа для миттєвих значень напружень і струмів, зв'язаних між собою на окремих елементах ланцюга співвідношеннями:
для резистора (ідеальний активний опір)
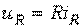 (2.1)
(2.1)
для котушки індуктивності (ідеальна індуктивність)
 (2.2)
(2.2)
для конденсатора (ідеальна місткість)
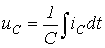 (2.3)
(2.3)
Для послідовного ланцюга, що містить лінійні резистор R, котушку індуктивності L і конденсатор С, при її підключенні до джерела з постійною напругою u (рис. 1.1) можна записати
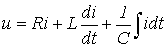 (2.4)
(2.4)
Диференціюючи цей вираз одержимо лінійне диференціальне рівняння другого порядку
 . (2.5)
. (2.5)
Порядок даного рівняння рівний числу незалежних накопичувачів енергії в ланцюзі. Під ними розуміються котушки індуктивності і конденсатори в спрощеній схемі, яку одержуємо з початкової шляхом об'єднання індуктивностей і відповідно ємностей елементів, з'єднання між якими є послідовними або паралельними.
У загальному випадку порядок диференціального рівняння визначається співвідношенням
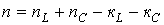 (2.6)
(2.6)
де 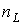 и
и  - відповідно число котушок індуктивності і конденсаторів після вказаного спрощення початкової схеми;
- відповідно число котушок індуктивності і конденсаторів після вказаного спрощення початкової схеми; 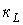 - число вузлів, в яких сходяться тільки гілки, що містять котушки індуктивності (відповідно до першого закону Кірхгофа струм через будь-яку котушку індуктивності в цьому випадку визначається струмами через решту котушок);
- число вузлів, в яких сходяться тільки гілки, що містять котушки індуктивності (відповідно до першого закону Кірхгофа струм через будь-яку котушку індуктивності в цьому випадку визначається струмами через решту котушок); 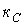 - число контурів схеми, гілки яких містять тільки конденсатори (відповідно до другого закону Кірхгофа напруга на будь-якому з конденсаторів в цьому випадку визначається напругою на інших).
- число контурів схеми, гілки яких містять тільки конденсатори (відповідно до другого закону Кірхгофа напруга на будь-якому з конденсаторів в цьому випадку визначається напругою на інших).
Наявність індуктивних зв'язків на порядок диференціального рівняння не впливає.
У рішенні рівняння (2.5) класичним методом примушена складова струму відсутня а форма запису вільної складової струму залежить від виду коріння характеристичного рівняння яке виходить шляхом заміни  на р2,
на р2,  - на р і р0 = 1.
- на р і р0 = 1.
LP2+RP+1/C=0 (2.7)
коріння цього характеристичного рівняння визначається як
Р1,2=  (2.8)
(2.8)
Позначивши
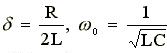
Одержимо
Р1,2=  (2.9)
(2.9)
Залежно від співвідношення d и w 0 можливі три випадки: а) d > w0, т.е.
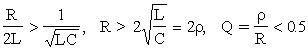 (аперіодичний процес).У площині комплексного змінного коріння характеристичного рівняння лежить на речовинній осі (рис.2.2).
(аперіодичний процес).У площині комплексного змінного коріння характеристичного рівняння лежить на речовинній осі (рис.2.2). 
Рисунок 2.2 – Положення коріння на комплексній площині при аперіодичному процесі
Напруга на елементах UR=Ri= (еp1t-еp2t), UL=L
(еp1t-еp2t), UL=L =
= 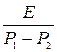 (P1еp1t-P2еp2t), UC=E-UR-UL=E[1+ (P2еp1--P1еp2t)].
(P1еp1t-P2еp2t), UC=E-UR-UL=E[1+ (P2еp1--P1еp2t)]. Графіки залежностей UR, UL, UC від часу приведені (рис.2.3).

Рисунок 2.3 - залежність UR, UL, UC від часу при аперіодичному процесі
б) d = w 0, R = 2d, Q = 0.5 (критичний режим),Р1,2 =-d, i(t)=
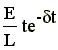 . Форма кривих залежностей струму і напруги на R, L, C від часу аналогічна аперіодичному режиму, умова Q=0.5 є граничною умовою існування в ланцюзі аперіодичних процесів;в)
. Форма кривих залежностей струму і напруги на R, L, C від часу аналогічна аперіодичному режиму, умова Q=0.5 є граничною умовою існування в ланцюзі аперіодичних процесів;в) 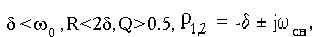 (коливальний процес).
(коливальний процес). Коріння характеристичного рівняння комплексно-зв'язане (рис.2.4).

Рисунок 2.4 - Положення коріння на комплексній площині при коливальному процесі
Струм в ланцюзі є затухаючим гармонійним коливанням, амплітуда якого зменшується в часі по експоненціальному закону (рис.2.5).


Рисунок 2.5 – Форма струму в ланцюзі є затухаючим гармонійним коливанням
Напруга на елементах ланцюга
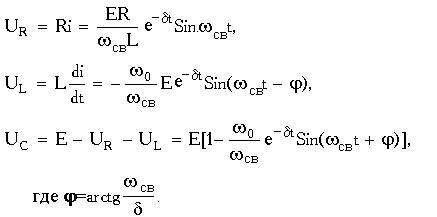 Графіки залежностей UR, UL, UC від часу приведені на рис.2.6.
Графіки залежностей UR, UL, UC від часу приведені на рис.2.6. 
Рисунок 2.6 - Графіки залежностей UR, UL, UC від часу при коливальному процесі
Швидкість зменшення амплітуди коливань оцінюють величиною декременту загасання Δ = eδTсв де Тсв - період вільних коливань, і логарифмічним декрементом загасання θ = ln Δ = δ Tсв = Tсв / τсв . при визначенні декремента загасання по експериментально одержаній осцилограмі струму його зручно знаходити як відношення амплітуд першого і другого періодів затухаючих коливань Δ = Im1 / Im2, як показано на рис 2.7,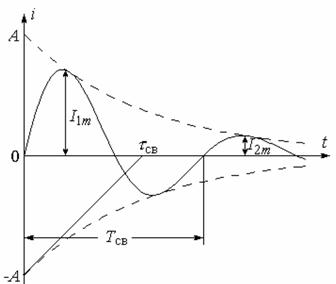
Рисунок 2.7 – До визначення декремента загасання
1.4 Порядок виконання роботи:
1. Зібрати (на екрані монітору ПК) у програмі Electronics Workbench за допомогою стандартизованих елементів (табл. 2.1), схему заданого електричного кола (рис 2.8).
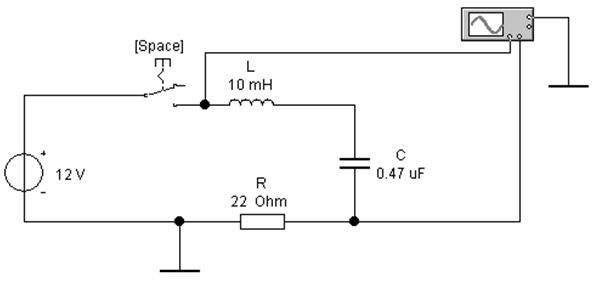
Рисунок 2.8 – Схема электрическая для исследования переходных процессов
2. Включити зібрану схему за допомогою перемикача  , або натиснувши на клавіатурі ПК кнопки Ctrl+G.
, або натиснувши на клавіатурі ПК кнопки Ctrl+G.
3. Натиснути клавішу «Пробел». на екрані віртуального осцилографа повинні з'явитися імпульс вхідної дії і сигнал реакції схеми на цю дію.
4. Вимкнути схему за допомогою того ж перемикача  , або натиснувши на клавіатурі ПК Ctrl+Т.
, або натиснувши на клавіатурі ПК Ctrl+Т.
5. за допомогою шкал віртуального осцилографа визначити амплітудні і часові характеристики перехідного процесу того, що протікає в схемі. Зарисувати одержані епюри напружень. Одержані дані занести в таблицю 1.2
Таблиця 2.1 – Початкові значення за варіантами
| №. варіанта | L, мГн | С, мкФ | R, Ом |
| 0,47 | |||
| 0,1 | |||
| 0,22 | |||
| 0,47 | |||
| 0,1 | |||
| 0,22 | |||
| 0,1 | |||
| 0,1 |
Таблиця 2.2 – Числові дані характеристик електричного кола
| Розрахункові дані | Експериментальні дані | ||||||||||
| Величина | Р1 | Р2 | f0 | δ | Tсв | Q | Im1 | Im2 | Tсв | δ | Q |
| Дані замірів: |
6. Показати на комплексній площині розташування коріння характеристичного рівняння. Зробити висновок про характер перехідного процесу.
7. розрахувати коефіцієнт загасання δ, частоту вільних коливань, а також постійну інтегрування А = Е / (ωСВL)
1.5 Зміст звіту
До звіту заносять:
- тему і мету роботи;
- принципову схему електричного кола, яке аналізується;
- теоретичний розрахунок параметрів електричного кола, яке аналізується
- результати вимірювання струмів та напруг на окремих ділянках досліджуваного кола;
- результати розрахунку параметрів перехідного процесу;
- епюри вхідної дії і перехідного процесу;
- висновки по роботі.
1.6 Контрольні питання
1. як складається характеристичне рівняння?
2. які види перехідних процесів можливі в RLC - ланцюгах залежно від виду коріння характеристичного рівняння.
3. як визначаються начальне умови для досліджуваної схемі?
4. Що характеризує декремент затухання і як він визначається?
5. як по значенню комплексного кореня визначити постійну часу обгинання?
6. як по значенню комплексного кореня визначити період вільних коливань?
Лабораторна робота №3
ДОСЛІДЖЕННЯ нелінійних ланцюгів ПОСТІЙНОГО СТРУМУ
2.1 Мета роботи:Експериментальне дослідження розподілу струмів і напружень в нелінійному електричному ланцюзі (ЕЛ) постійного струму. Визначення струмів і напружень в нелінійному ЕЛ графоаналітичними методами.
2.2 Зміст роботи:
Для заданого електричного кола (рис.3.1):
- встановити задані параметри джерела живлення електричного кола;
- провести необхідні вимірювання величин струмів та напруги;
- розрахувати параметри кола постійного струму з нелінійними елементами;
- оцінити похибки вимірювань та зробити висновки щодо режимів роботи лінії. При оцінці похибок вимірювань вважати межею вимірювань Iмах = 1А (для амперметрів), Vмах = 10 В (для вольтметрів), а за клас точності прийняти для всіх приладів δ = 0,1.
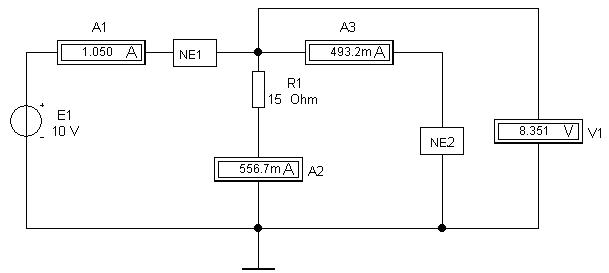
Рисунок 3.1– Принципова електрична схема кола для дослідження
2.3 Теоретичні відомості:
ЕЛ звуться нелінійними, якщо в ланцюзі є хоч би один нелінійний елемент (НЕ). У таких елементів вольт-амперна характеристика (ВАХ) (I = f (U)) є нелінійною функцією, оскільки опір цього елементу залежить від величини і напряму струму, що протікає через нього, або від величини і знаку напруги, прикладеної до нього. Нелінійні елементи описуються нелінійними характеристиками, які не мають строгого аналітичного виразу, визначаються експериментально і задаються табличний або графіками.
Нелінійні елементи можна розділити на двох - і багатополюсні. Останні містять три (різні напівпровідникові і електронні тріоди) і більш (магнітні підсилювачі, трансформатори з багатьма обмотками, тетроди, пентоди і ін.) полюсів, за допомогою яких вони підключаються до електричного ланцюга. Характерною особливістю багатополюсних елементів є те, що в загальному випадку їх властивості визначаються сімейством характеристик, що представляють залежності вихідних характеристик від вхідних змінних і навпаки: вхідні характеристики будують для ряду фіксованих значень одного з вихідних параметрів, вихідні - для ряду фіксованих значень одного з вхідних.
За іншою ознакою класифікації нелінійні елементи можна розділити на інерційні і неінерційні. Інерційними називаються елементи, характеристики яких залежать від швидкості зміни змінних. Для таких елементів статичні характеристики, що визначають залежність між діючими значеннями змінних, відрізняються від динамічних характеристик, що встановлюють взаємозв'язок між миттєвими значеннями змінних. Неінерційними називаються елементи, характеристики яких не залежать від швидкості зміни змінних. Для таких елементів статичні і динамічні характеристики співпадають.
Залежно від виду характеристик розрізняють нелінійні елементи з симетричними і несиметричними характеристиками. Симетричною називається характеристика, не залежна від напряму визначальних її величин, тобто що має симетрію відносно почала системи координат: 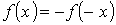 . Для несиметричної характеристики ця умова не виконується, тобто
. Для несиметричної характеристики ця умова не виконується, тобто 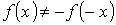 . Наявність у нелінійного елементу симетричної характеристики дозволяє у цілому ряді випадків спростити аналіз схеми, здійснюючи його в межах одного квадранта.
. Наявність у нелінійного елементу симетричної характеристики дозволяє у цілому ряді випадків спростити аналіз схеми, здійснюючи його в межах одного квадранта.
У сучасних засобах автоматики, радіотехніки і обчислювальної техніки широке застосування знаходять НЕ (діоди, транзистори, тиристори і т.д.), які мають різні по формі ВАХ.
Поиск по сайту: