Тема 1 Философия в системе культуры

Немецкий физик И. Фраунгофер (1787-1826) рассмотрел дифракцию плюсках световых волн, или дифракцию в параллельных лучах. Дифракция Фраунгофера, имеющая большое практическое значение, наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию. Чтобы этот тип дифракции осуществить, достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.

Рассмотрим дифракцию Фраунгофера от бесконечно длинной щели (для этого практически достаточно, чтобы длина щели была значительно больше ее ширины). Пусть плоская монохроматическая световая волна падает нормально плоскости узкой щели шириной а (рис. 261, а). Оптическая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении j,

(179.1)

где F- основание перпендикуляра, опущенного из точки М на луч ND.

Рис. 261

Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна l/2, т. е. всего на ширине щели уместится D:l/2 зон. Так как свет на щель падает нормально, то плоскость щели совпадает с волновым фронтом; следовательно, все точки волнового фронта в плоскости щели будут колебаться в одинаковой фазе. Амплитуды вторичных волн в плоскости щели будут равны, так как выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения.

Из выражения (179.1) вытекает, что число зон Френеля, укладывающихся на ширине щели, зависит от угла j. От числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн. Из приведенного построения следует, что при интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно гасят друг друга. Следовательно, если число зон Френеля четное, то

(179.2)

и в точке В наблюдается дифракционный минимум (полная темнота), если же число зон Френеля нечетное, то

(179.3)

и наблюдается дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля. Отметим, что в направлении j = 0щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсивностью, т. е. в точке В₀наблюдается центральный дифракционный максимум.

Из условий (179.2) и (179.3) можно найти направления на точки экрана, в которых амплитуда (а следовательно, и интенсивность) равна нулю (sinj_min = ± ml/a) или максимальна sinj_min = ± (2m + 1) l/(2a).Распределение интенсивности на экране, получаемое вследствие дифракции (дифракционный спектр), приведено на рис. 261, б. Расчеты показывают, что интенсивности в центральном и последующих максимумах относятся как 1: 0,047: 0,017: 0,0083:..., т. е. основная часть световой энергии сосредоточена в центральном максимуме. Из опыта и соответствующих расчетов следует, что сужение щели приводит к тому, что центральный максимум расплывается, а интенсивность уменьшается (это, естественно, относится и к другим максимумам). Наоборот, чем щель шире (а > l),тем картина ярче, но дифракционные полосы уже, а число самих полос больше. При а ≫l в центре получается резкое изображение источника света, т. е. имеет место прямолинейное распространение света.

Положение дифракционных максимумов зависит от длины волны l, поэтому рассмотренная выше дифракционная картина имеет место лишь для монохроматического света. При освещении щели белым светом центральный максимум наблюдается в виде белой полоски; он общий для всех длин волн (при j = 0 разность хода равна нулю для всех l). Боковые максимумы радужно окрашены, так как условие максимума при любых mразлично для разныхl. Таким образом, справа и слева от центрального максимума наблюдаются максимумы первого (m = 1), второго (m = 2) и других порядков, обращенные фиолетовым краем к центру дифракционной картины. Однако они настолько расплывчаты, что отчетливого разделения различных длин волн с помощью дифракции на одной щели получить невозможно.

13. ДИФРАКЦИЯ ФРАУНГОФЕРА НА ДИФРАКЦИОННОЙ РЕШЕТКЕ Условие главных максимумов дифракционной решетки.

Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через одномерную дифракционную решетку - систему параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками. Рассматривая дифракцию Фраунгофера на щели, мы видели, что распределение интенсивности на экране определяется направлением дифрагированных лучей. Это означает, что перемещение щели параллельно самой себе влево или вправо не изменит дифракционной картины. Следовательно, если перейти от одной щели ко многим (к дифракционной решетке), то дифракционные картины, создаваемые каждой щелью в отдельности, будут одинаковыми.

Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т. е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.

Рассмотрим дифракционную решетку. На рис. 262 для наглядности показаны только две соседние щели MN и CD. Если ширина каждой щели равна а, а ширина непрозрачных участков между щелями b, то величина d = a + bназывается постоянной (периодом) дифракционной решетки.

Рис. 262

Пусть плоская монохроматическая волна падает нормально к плоскости решетки. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления jодинаковы в пределах всей дифракционной решетки:

(180.1)

Очевидно, что в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т. е. прежние (главные) минимумы интенсивности будут наблюдаться в направлениях, определяемых условием (179.2):

(180.2)

Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т. е. возникнут дополнительные минимумы. Очевидно, что эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода лучей l/2, З l/2, …, посылаемых, например, от крайних левых точек М и С обеих щелей. Таким образом, с учетом (180.1) условие дополнительных минимумов:

Наоборот, действие одной щели будет усиливать действие другой, если

(180.3)

т. е. выражение (180.3) задает условие главных максимумов.

Таким образом, полная дифракционная картина для двух щелей определяется из условий:

т. е. между двумя главными максимумами располагается один дополнительный минимум. Аналогично можно показать, что между каждыми двумя главными максимумами при трех щелях располагается два дополнительных минимума, при четырех щелях - три и т. д.

Если дифракционная решетка состоит из N щелей, то условием главных минимумов является условие (180.2), условием главных максимумов - условие (180.3), а условием дополнительных минимумов

(180.4)

где т' может принимать все целочисленные значения, кроме 0, N, 2N ,.... т. е. кроме тех, при которых условие (180.4) переходит в (180.3). Следовательно, в случае N щелей между двумя главными максимумами располагается N- 1 дополнительных минимумов, разделенных вторичными максимумами, создающими весьма слабый фон.

Чем больше щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется между соседними главными максимумами, тем, следовательно, более интенсивными и более острыми будут максимумы. На рис. 263 качественно представлена дифракционная картина от восьми щелей. Так как модуль sinjне может быть больше единицы, то из (180.3) следует, что число главных максимумов

т. е. определяется отношением периода решетки к длине волны.

Рис. 263

Положение главных максимумов зависит от длины волны l (см. (180.3)). Поэтому при пропускании через решетку белого света все максимумы, кроме центрального (m = 0), разложатся в спектр, фиолетовая область которого будет обращена к центру дифракционной картины, красная - наружу. Это свойство дифракционной решетки используется для исследования спектрального состава света (определения длин волн и интенсивностей всех монохроматических компонентов), т. е. дифракционная решетка может быть использована как спектральный прибор.

Дифракционные решетки, используемые в различных областях спектра, отличаются размерами, формой, материалом поверхности, профилем штрихов и их частотой (от 6000 до 0,25 штрих/мм, что позволяет перекрывать область спектра от ультрафиолетовой его части до инфракрасной). Например, ступенчатый профиль решетки позволяет концентрировать основную часть падающей энергии в направлении одного определенного ненулевого порядка.

14.Пространственная решетка. Рассеяние света

Дифракция света наблюдается не только на плоской одномерной решетке (штрихи нанесены перпендикулярно некоторой прямой линии), но и на двумерной решетке (штрихи нанесены во взаимно перпендикулярных направлениях в одной и той же плоскости). Большой интерес представляет также дифракция на пространственных (трехмерных) решетках — пространственных образованиях, в которых элементы структуры подобны по форме, имеют геометрически правильное и периодически повторяющееся расположение, а также постоянные (периоды) решеток, соизмеримые с длиной волны электромагнитного излучения. Иными словами, подобные пространственные образования должны иметь периодичность по трем не лежащим в одной плоскости направлениям. В качестве пространственных дифракционных решеток могут быть использованы кристаллические тела, так как в них неоднородности (атомы, молекулы, ионы) регулярно повторяются в трех направлениях.

Дифракция света может происходить также в так называемых мутных средах — средах с явно выраженными оптическими неоднородностями. К мутным средам относятся аэрозоли (облака, дым, туман), эмульсия, коллоидные растворы и т. д., т. е. такие среды, в которых взвешено множество очень мелких частиц инородных веществ. Свет, проходя через мутную среду, дифрагирует от беспорядочно расположенных микронеоднородностей, давая равномерное распределение интенсивностей по всем направлениям, не создавая какой-либо определенной дифракционной картины. Происходит так называемое рассеяние света в мутной среде. Это явление можно наблюдать, например, когда узкий пучок солнечных лучей, проходя через запыленный воздух, рассеивается на пылинках и тем самым становится видимым.

Рассеяние света (как правило, слабое) наблюдается также и в чистых средах, не содержащих посторонних частиц. Л. И. Мандельштам объяснил рассеяние света в средах нарушением их оптической однородности, при котором показатель преломления среды не постоянен, а меняется от точки к точке. В дальнейшем польский физик М. Смолуховский (1872—1917) указал, что причиной рассеяния света могут быть также флуктуации плотности, возникающие в процессе хаотического (теплового) движения молекул среды. Рассеяние света в чистых средах, обусловленное флуктуациями плотности, анизотропии или концентрации, называется молекулярным рассеянием.

Молекулярным рассеянием объясняется, например, голубой цвет неба. Согласно закону Д. Рэлея, интенсивность рассеянного света обратно пропорциональна четвертой степени длины волны (I~l–4), поэтому голубые и синие лучи рассеиваются сильнее, чем желтые и красные, обусловливая тем самым голубой цвет неба. По этой же причине свет, прошедший через значительную толщу атмосферы, оказывается обогащенным более длинноволновой частью спектра (сине-фиолетовая часть спектра полностью рассеивается) и поэтому при закате и восходе Солнце кажется красным. Флуктуации плотности и интенсивность рассеяния света возрастают с увеличением температуры. Поэтому в ясный летний день цвет неба является более насыщенным по сравнению с таким же зимним днем.

15.Дисперсия света.

Диспе́рсия све́та (разложение света) — это явление, обусловленное зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты). Экспериментально открыта Ньютоном около 1672 года, хотя теоретически достаточно хорошо объяснена значительно позднее.

· Пространственной дисперсией называется зависимость тензора диэлектрической проницаемости среды от волнового вектора. Такая зависимость вызывает ряд явлений, называемых эффектами пространственной поляризации.

Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Сущностью явления дисперсии является различие скоростей распространения лучей света c различной длиной волны в прозрачном веществе — оптической среде (тогда как в вакууме скорость света всегда одинакова, независимо от длины волны и следовательно цвета). Обычно, чем больше частота световой волны, тем больше показатель преломления среды для неё и тем меньше скорость волны в среде:

· у света красного цвета скорость распространения в среде максимальна, а степень преломления — минимальна,

· у света фиолетового цвета скорость распространения в среде минимальна, а степень преломления — максимальна.

Однако в некоторых веществах (например в парах иода) наблюдается эффект аномальной дисперсии, при котором синие лучи преломляются меньше, чем красные, а другие лучи поглощаются веществом и от наблюдения ускользают. Говоря строже, аномальная дисперсия широко распространена, например, она наблюдается практически у всех газов на частотах вблизи линий поглощения, однако у паров иода она достаточно удобна для наблюдения в оптическом диапазоне, где они очень сильно поглощают свет.

Дисперсия света позволила впервые вполне убедительно показать составную природу белого света.

· Белый свет разлагается в спектр и в результате прохождения через дифракционную решётку или отражения от нее (это не связано с явлением дисперсии, а объясняется природой дифракции). Дифракционный и призматический спектры несколько отличаются: призматический спектр сжат в красной части и растянут в фиолетовой и располагается в порядке убывания длины волны: от красного к фиолетовому; нормальный (дифракционный) спектр — равномерный во всех областях и располагается в порядке возрастания длин волн: от фиолетового к красному.

По аналогии с дисперсией света, также дисперсией называются и сходные явления зависимости распространения волн любой другой природы от длины волны (или частоты). По этой причине, например, термин закон дисперсии, применяемый как название количественного соотношения, связывающего частоту и волновое число, применяется не только к электромагнитной волне, но к любому волновому процессу.

Дисперсией объясняется факт появления радуги после дождя (точнее тот факт, что радуга разноцветная, а не белая).

Дисперсия является причиной хроматических аберраций — одних из аберраций оптических систем, в том числе фотографических и видео-объективов.

Огюстен Коши предложил эмпирическую формулу для аппроксимации зависимости показателя преломления среды от длины волны:

,

где 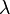— длина волны в вакууме; a, b, c — постоянные, значения которых для каждого материала должны быть определены в опыте. В большинстве случаев можно ограничиться двумя первыми членами формулы Коши. Впоследствии были предложены другие более точные, но и одновременно более сложные, формулы аппроксимации.

16. Поляризация света.

I. П. света названо было явление особого видоизменения естественных световых лучей, исходящих от обыкновенного источника света, при котором лучи приобретают как бы различные свойства по различным направлениям, перпендикулярным к направлению луча; такое свойство лучей может быть вызвано в самом источнике света, если поставить последний в некоторые определенные условия (см. ниже), но оно может быть искусственно придано и лучам, вышедшим из источника света в естественном их состоянии. Общепринятая теория света Френеля, объясняющая явления света колебанием частиц эфира, передачей колебания от частицы к частице и являющимся, таким образом, распространением в эфире волн, вполне объясняет и явление П. света предположением о различной возможной форме путей колебания частиц эфира. Эта теория предполагает, что в неполяризованном естественном луче частицы эфира колеблются каждая в плоскости перпендикулярной к лучу J (фиг. 1) по прямой линии, проходящей через положение равновесия частицы; направление этой прямой линии непрерывно и чрезвычайно быстро переходит из одного положения a в другое b, далее в с и т. д., но оставаясь постоянно в одной плоскости; подробности о возможных формах колебания частиц у естественного луча см. Свет.

Фиг. 1. Фиг. 2.

Если колебания частиц эфира происходят не по всем прямым, возможным в плоскости А, перпендикулярной к лучу (фиг. 2), а постоянно лишь по одной прямой ab, то мы говорим, что луч прямолинейно поляризован: плоскость ВВ, проходящую через луч и путь колебания частицы, называем плоскостью колебания прямолинейно поляризованного луча; плоскость же СС, проходящую тоже через луч и перпендикулярную к плоскости колебаний, принято наз. плоскостью П. луча [Плоскость II. представляет, в сущности, самостоятельное понятие, не связанное генетически с понятием о плоскости колебания. Теория Френеля и полагает, что плоскость П. перпендикулярна к плоскости колебания, теория же Неймана полагает, что они совпадают. Первая теория более общепринята; подробнее см. Свет]. Таким образом, луч естественный мы можем себе представить, как луч прямолинейно поляризованный, у которого плоскость колебания, а следовательно, и плоскость П. непрерывно меняются. Когда частица эфира движется вокруг своего положения равновесия о, описывая непрерывно в плоскости, перпендикулярной к лучу, один и тот же эллипс (фиг. 3), то мы говорим, что это луч и свет эллиптически поляризованный.

Фиг. 3. Фиг. 4.

Эллипс этот может быть весьма различного вида; он может быть весьма растянутым и в конце концов перейти в прямую линию (прямолинейно поляризованный луч); или обе оси его могут быть равны, и тогда эллипс перейдет в круг и свет называется поляризованным по кругу (фиг. 4). Распространение колебания в случае луча, поляризованного эллиптически или по кругу, нужно себе представить так, как это изображено на ф. 5.

Фиг. 5.

Точки о, а, b, с, d суть положения равновесия эфирных частиц на луче AB движущихся по окружности эллипсов, плоскости которых перпендикулярны к лучу. Когда частица о находится в положении о', то частица a находится в а", а положения частиц b, с, d будут b", с", d". Если мы эти положения соединим непрерывной чертой, то получим винтовую линию, начерченную на эллиптическом цилиндре. Через мгновение а, двигаясь по направлению стрелки, из а" придет в а', настолько же передвинутся другие частицы, и винтовая линия повернется на а"а' вокруг AB.

17.Закон Малюса

Закон Малюса — физический закон, выражающий зависимость интенсивности линейно-поляризованного света после его прохождения через поляризатор от угла между плоскостями поляризации падающего света и поляризатора.

где 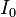— интенсивность падающего на поляризатор света, — интенсивность света, выходящего из поляризатора, — коэффициент пропускания поляризатора.

Установлен Э. Л. Малюсом в 1810 году.

В релятивистской форме

где и — циклические частоты линейно поляризованных волн, падающей на поляризатор и вышедшей из него.

Свет с иной (не линейной) поляризацией может быть представлен в виде суммы двух линейно-поляризованных составляющих, к каждой из которых применим закон Малюса. По закону Малюса рассчитываются интенсивности проходящего света во всех поляризационных приборах, например в поляризационных фотометрах и спектрофотометрах. Потери на отражение, зависящие от и не учитываемые законом Малюса, определяются дополнительно.

18. Поляризация света при отражении и преломлении на границе двух прозрачных диэлектриков. Закон Брюстера

Зако́н Брю́стера — закон оптики, выражающий связь показателей преломления двух диэлектриков с таким углом падения света, при котором свет, отражённый от границы раздела диэлектриков, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения. При этом преломлённый луч частично поляризуется в плоскости падения, и его поляризация достигает наибольшего значения (но не 100%, поскольку от границы отразится лишь часть света, поляризованного перпендикулярно к плоскости падения, а оставшаяся часть войдёт в состав преломлённого луча). Угол падения, при котором отражённый луч полностью поляризован, называется углом Брюстера ^[1]. При падении под углом Брюстера отражённый и преломлённый лучи взаимно перпендикулярны.

Это явление оптики названо по имени шотландского физика Дэвида Брюстера, открывшего его в 1815 году.

Поляризующий эффект можно понять, если иметь в виду следующее:

· колебания электрического поля в электромагнитной волне всегда происходят перпендикулярно направлению движения.

· Взаимодействие с диэлектриком происходит в два этапа. В начале падающая волна генерирует коллективные колебания дипольных моментов молекул диэлектрика, затем эти осцилляции в свою очередь генерируют отражённую и преломлённую волну.

Итак, отражённая волна генерируется колебаниями дипольных моментов молекул среды. Когда угол между отражённой и преломленной волной составляет 90 градусов, колебания электрического поля отражённой волны в плоскости падения могли бы генерироваться только колебаниями дипольных моментов вдоль преломлённого луча. Индуцировать такие колебания могла бы только продольная компонента колебаний электрического поля преломлённого луча. Но поскольку в преломленном пучке её нет, то и в отражённом не может быть.

Закон Брюстера записывается в виде:

где — показатель преломления второй среды относительно первой, а — угол падения (угол Брюстера).

При падении света на одну пластинку под углом Брюстера интенсивность отражённого линейно поляризованного света очень мала (для границы воздух-стекло — около 4 % от интенсивности падающего луча). Поэтому для того, чтобы увеличить интенсивность отраженного света (или поляризовать свет, прошедший в стекло, в плоскости, параллельной плоскости падения) применяют несколько скрепленных пластинок, сложенных в стопу — стопу Столетова. Легко проследить по чертежу происходящее. Пусть на верхнюю часть стопы падает луч света. От первой пластины будет отражаться полностью поляризованный луч (около 4 % первоначальной интенсивности), от второй пластины также отразится полностью поляризованный луч (около 3,75 % первоначальной интенсивности) и так далее. При этом луч, выходящий из стопы снизу, будет все больше поляризоваться в плоскости, параллельной плоскости падения, по мере добавления пластин.

Две фотографии оз. Чёрного, сделанные фотоаппаратом без поляризующего фильтра и с ним. На правой фотографии он повёрнут таким образом, что отражённый свет почти полностью отфильтровывается и блики исчезают.

Закон Брюстера можно вывести из формул Френеля, описывающих зависимость амплитуды, фазы и поляризации отражённой и преломлённой световых волн от соответствующих характеристик волны, падающей на границу раздела диэлектриков.

19.Двойное лучепреломление.

Двойно́е лучепреломле́ние — эффект расщепления в анизотропных средах луча света на две составляющие. Впервые обнаружен датским ученым Расмусом Бартолином на кристалле исландского шпата. Если луч света падает перпендикулярно к поверхности кристалла, то на этой поверхности он расщепляется на два луча. Первый луч продолжает распространяться прямо, и называется обыкновенным (o — ordinary), второй же отклоняется в сторону, и называется необыкновенным (e — extraordinary).

Тема 1 Философия в системе культуры

В качестве важнейшей предпосылки формирования гре­ческой философии как становления свободного духа древних греков является выработанная ими такая форма политического правления, как демократия. Особенности политического устройства Древней Греции привели к активной политической и культурной жизни, к элементам демократии и публичности в принятии решений, что часто проявилось в виде открытых споров и дискуссий. Агональ­ность (соревновательность) пронизывает философию, которая принимает диалоговую форму, основанную на столкновении разных точек зрения. А это в свою оче­редь, дает начало, с одной стороны, доказательному типу мышления основанному на разработке разнообразных приемов и типов доказательств, что позже связывается с такой философской дисциплиной, как логика. А с другой — дополняет логическое доказательство психико-эмоциональными приемами воздействия на сознание человека, что при­водит к становлению такой дисциплины, как риторика.

В Древней Греции становление философии было связано с рационалисти­ческим преодолением мифологического сознания. Установка мифа иа целостное понимание бытия и места в нем человека глубоко протаи­вает философию, отличая ее уже с самого начала от дифференцированного, предметного подхода наук. Для философии становятся важными не только знания, но и сфера эмоциональных пе­реживаний человека, от которых человек никогда не сможет оконча­тельно освободиться.

Все это в совокупности дает нам еще один аргумент в пользу выбора именно античной философии Греции в качестве модели становления философии. Дело в том, что рационалистическая установка древнегреческой культуры, в центре которой находилась соответствующая философия, дала начало тому, что мы сегодня называем цивилизацией.

Поиск по сайту: