Плотность состояний

Все основные свойства электронных нитей оп­ределяются их законом дисперсии, т. е. зависи­мостью энергии от импульса, определяемой формулой (4.1). В этой связи очень интересно сравнить между собой электронные системы различных размернос­тей: массивные полупроводники с законом диспер­сии Е = (р²_х + р²_y + р²_z)/2т, двумерные структуры с законом дисперсии Е= E_N + (p²_x + р²_у)/2т и кван­товые нити. Несмотря на внешнее сходство приведенных формул, разное число направлений, по которым электроны могут свободно двигаться, вызовет качественное различие почти во всех свойствах.

Важнейшей характеристикой электронной сис­темы наряду с ее законом дисперсии является плот­ность состояний, т. е. число состояний в еди­ничном интервале энергии. Поскольку электроны подчиняются принципу Паули, то плотность состоя­ний определит то максимальное число электронов, которое может разместиться в данном интервале энергий, а уж распределение электронов по энерги­ям определит все их остальные свойства.

Основной вопрос здесь заключается в следую­щем: насколько должны отличаться импульсы двух электронов, чтобы они могли считаться принадле­жащими к различным квантовым состояниям и не подчиняться принципу Паули? Пусть размер образ­ца вдоль оси х равен L_x. Из соотношений неопреде­ленности квантовой механики следует, что при этом неопределенность импульса р_х будет равна 2πћ/L_x и, следовательно, различными могут считаться со­стояния со значениями импульса, различающими­ся на 2πћ/L ^[1] . Аналогичные рассуждения относят­ся и к другим направлениям, в которых электроны двигаются как свободные.

Теперь можно вычислить важную промежу­точную характеристику системы G(E) – полное число состояний, имеющих энергию, меньшую, чем Е. В трехмерном случае:

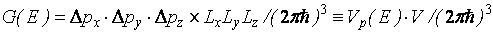, (4.2)

где V – объем об­разца, a V_p – объем так называемого импульсного пространства, т. е. области в осях р_х, р_у, p_z, 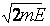, для которой энергия электрона (р_х ²+ p_y² + р_z²)/2т мень­ше, чем Е. Легко понять, что эта область представ­ляет собой шар радиусом и объемом (4π/3)(2тЕ)^3/2, так что окончательно в трехмерном случае .

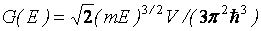Очевидно, что G(E) образовалось суммировани­ем всех состояний с энергиями от 0 до Е. При этом плотность состояний вблизи за­данной энергии будет определяться производной G по энергии. Кроме того, обычно возникает необходимость знать плотность состояний в расчете не на весь образец, а на единицу объема и учитывать то, что в каждом состоянии могут находиться два электрона с проти­воположными спинами. Это дает окончательную формулу для трехмерной плотности состояний:

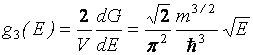. (4.3)

В двумерном случае для каждого из квантово-размерных уровней с энергией E_N полное число со­стояний G_N(E)= m(E – E_N)S/(2πћ²), S – площадь об­разца. Плотность состояний, которая в этом случае вычисляется на единицу площади, определяется суммой по всем уровням, энергии которых E_N лежат ниже Е:

. (4.4)

Наконец, для каждого уровня энергии Е_i 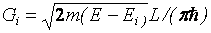квантовой нити длиной L и плотность состояний на единицу длины

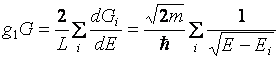. (4.5)

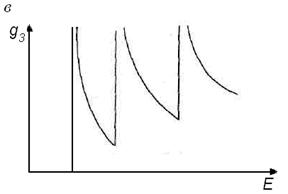
На рис. 4.2 схематично показаны функции плотности состояний для всех обсуждавшихся случаев. Видно, что они носят качественно различный характер.

	Рис. 4.2.Плотность состояний в массивном трех­мерном полупроводнике (а), в двумерных элек­тронных структурах – квантовых ямах (б) и одно­мерных структурах – квантовых нитях (в)

В трехмерном случае плотность состояний монотонно растет с энергией, в двумерном случае имеет вид горизонтальных ступенек, а в квантовых нитях неограниченно растет каждый раз, если необходимо сделать оценку величины энергии очередного кванто­вого уровня.

№45

Поиск по сайту: