Понятие о квантовой статистике Бозе - Эйнштейна и Ферми - Дирака

Одним из важнейших «объектов» изучения квантовой статистики, как и классической, является идеальный газ. Это связано с тем, что во многих случаях реальную систему можно в хорошем приближении считать идеальным газом. Состояние системы невзаимодействующих частиц задается с помощью так называемых чисел заполнения N_i — чисел, указывающих степень заполнения квантового состояния (характеризуется данным набором i квантовых чисел) частицами системы, состоящей из многих тождест­венных частиц. Для систем частиц, образованных бозонами — частицами с нулевым или целым спином, числа заполнения могут принимать любые целые значения: 0, 1, 2,.... Для систем частиц, образованных фермионами — частицами с полуцелым спином, числа заполнения могут принимать лишь два значения: 0 для свободных состояний и 1 для занятых. Сумма всех чисел заполнения должна быть равна числу частиц системы. Квантовая статистика позволяет подсчитать среднее число частиц в данном квантовом состоянии, т. е. определить средние числа заполнения á N_i ñ.

Идеальный газ из бозонов — бозе-газ — описывается квантовой статистикой Бозе - Эйнштейна. * Распределение бозонов по энергиям вытекает из так называемого большого канонического распределения Гиббса (с переменным числом частиц) при условии, что число тождественных бозонов в данном квантовом состоянии может быть любым:

(235.1)

* Ш. Бозе (1894—1974) — индийский физик.

Это распределение называется распределением Бозе - Эйнштейна. Здесь á N_i ñ — сред­нее число бозонов в квантовом состоянии с энергией E_i, k — постоянная Больцмана, Т— термодинамическая температура, m —химический потенциал; m не зависит от энергии, а определяется только температурой и плотностью числа частиц. Химический потенциал находится обычно из условия, что сумма всех á N_i ñ равна полному числу частиц в системе. Здесь m £ 0, так как иначе среднее число частиц в данном квантовом состоянии отрицательно, что не имеет физического смысла. Он определяет изменение внутренней энергии системы при добавлении к ней одной частицы при условии, что все остальные величины, от которых зависит внутренняя энергия (энтропия, объем), фик­сированы.

Идеальный газ из фермионов — ферми-газ — описывается квантовой статистикой Ферми - Дирака. * Распределение фермионов по энергиям имеет вид

(235.2)

где á N_i ñ — среднее число фермионов в квантовом состоянии с энергией Е_i, m — химический потенциал. В отличие от (235.1) m может иметь положительное значение (это не приводит к отрицательным значениям чисел á N_i ñ). Это распределение называется распределением Ферми - Дирака.

* Э. Ферми (1901—1954) — итальянский физик.

Если >>1, то распределения Бозе - Эйнштейна (235.1) и Ферми - Дирака (235.2) переходят в классическое распределение Максвелла - Больцмана:

(235.3)

(ср. с выражением (44.4)), где

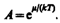(235.4)

Таким образом, при высоких температурах оба «квантовых» газа ведут себя подобно классическому газу.

Система частиц называется вырожденной, если ее свойства существенным образом отличаются от свойств систем, подчиняющихся классической статистике. Поведение как бозе-газа, так и ферми-газа отличается от классического газа, они являются вырожденными газами. Вырождение газов становится существенным при весьма низ­ких температурах и больших плотностях. Параметром вырождения называется величина А. При А <<1, т. е. при малой степени вырождения, распределения Бозе - Эйнштейна (235.1) и Ферми - Дирака (235.2) переходят в классическое распределение Максвелла - Больцмана (235.3).

Температурой вырождения Т ₀ называется температура, ниже которой отчетливо проявляются квантовые свойства идеального газа, обусловленные тождественностью частиц, т. е. Т ₀ — температура, при которой вырождение становится существенным. Если Т >> Т ₀, то поведение системы частиц (газа) описывается классическими законами.

Поиск по сайту: