АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Менеджмент и управление: сущность и проблематика

Читайте также:
  1. I. Социально-психологическая сущность неуставных взаимоотношений
  2. Аграрная модернизация в начале ХХ в.: предпосылки, сущность, итоги.
  3. Аграрная реформа правительства П.А. Столыпина: предпосылки, сущность, историческое значение
  4. АДМИНИСТРАТИВНЫЕ МЕТОДЫ УПРАВЛЕНИЯ, ИХ СУЩНОСТЬ, ДОСТОИНСТВА И НЕДОСТАТКИ
  5. Административные, социально-психологические и воспитательные методы менеджмента
  6. Административный процесс: сущность и виды
  7. Адміністративні методи менеджменту
  8. Азиатский стиль менеджмента
  9. Аксиомы науки о безопасности жизнедеятельности. Определение и сущность.
  10. Анализ основных тенденций в практике глобального стратегического инновационного менеджмента
  11. АНАЛИЗ ФУНКЦИЙ СПЕЦИАЛИСТОВ ПО СТРАТЕГИЧЕСКОМУ МЕНЕДЖМЕНТУ И ПОЛНОМОЧИЙ ОРГАНОВ УПРАВЛЕНИЯ ОРГАНИЗАЦИИ, ПРИНИМАЮЩИХ СТРАТЕГИЧЕСКИЕ РЕШЕНИЯ.
  12. Аннотация на учебное пособие «Экологический менеджмент»

 
 


Задача 6. Определить прогиб свободного конца балки переменного сечения (рис. 6). Данные взять из табл. 7.

Указания. Проще всего задачу можно решить графоаналитическим методом, построив эпюру M/EJ и приняв ее за фиктивную нагрузку. Левый конец фиктивной балки должен быть свободен, а правый – защемлен.

Рисунок 6 – Схемы балок переменного сечения

Таблица 7

№ строки Схема по рис.6 a b k
  I. 0,1 0,1 1,5
  II. 0,2 0,2  
  III. 0,3 0,3  
  IV. 0,4 0,4  
  V. 0,5 0,5  
  VI. 0,6 0,6  
  VII. 0,7 0,7  
  VIII. 0,8 0,8  
  IX. 0,9 0,9  
  X. 1,0 1,0  
  е г е д

Задача 7. Для балки, изображенной на рис. 7, требуется: 1) найти изгибающий момент на левой опоре (в долях ql2); 2) построить эпюры Q и М; 3)построить эпюру прогибов, вычислив три ординаты в пролете и две – на консоли. Данные взять из табл.7

Указания. Для ответа на первый вопрос нужно выбрать основную систему в виде свободно лежащей на двух опорах балки и составить уравнение деформаций, выражающее мысль, что суммарный угол поворота на левой опоре от заданной нагрузки и от опорного момента равен нулю.

Можно также решить задачу иначе, составив два уравнения: 1) уравнение статики в виде суммы моментов всех сил относительно правой опоры; 2) уравнение метода начальных параметров, выражающее мысль, что прогиб на правой опоре равен нулю. Из этих двух уравнений можно найти изгибающий момент и реакцию на левой опоре.

Для ответа на третий вопрос целесообразнее использовать метод начальных параметров, так как два начальных параметра (у0 и q0) известны.

При построении эпюры прогибов надо учесть, что упругая линия балки обращена выпуклостью вниз там, где изгибающий момент положительный, и выпуклостью вверх там, где он отрицательный. Нулевым точкам эпюры М соответствуют точки перегиба упругой линии.

Рисунок 7 – Схемы балок

 

Задача 8. Короткая бетонная колонна, поперечное сечение которого изображено на рис. 8, сжимается продольной силой F, приложенной в точке А. Требуется:1) вычислить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении, выразив эти напряжения через F и размеры сечения; 2) найти допускаемую нагрузку F при заданных размерах сечения и расчётных сопротивлениях для материала на сжатие Rc и на растяжение Rp. Данные взять из табл. 8.

 
 

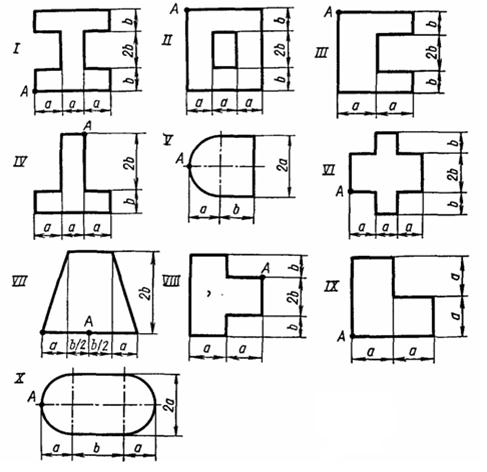
Рисунок 8 – Схемы колонн

Таблица 8

№ строки Схема по рис.8 a b Rс Rр
см МПа
  I.       4,0
  II.       3,5
  III.       3,0
  IV.       3,2
  V.       2,5
  VI.       2,0
  VII.       3,5
  VIII.       4,0
  IX.       3,2
  X.       2,5
  е г д е д

Задача 9. На рис. 9 изображена в аксонометрии ось ломаного стержня круглого поперечного сечения, расположенная в горизонтальной плоскости, с прямыми углами в точках A и В. На стержень действует вертикальная нагрузка. Требуется: 1) построить отдельно (в аксонометрии) эпюры изгибающих и крутящих моментов; 2) установить опасное сечение и найти для него расчетный момент по четвертой теории прочности. Данные взять из табл. 9.


Рисунок 9 – Схемы ломаных стержней

Таблица 9

№ строки Схема по рис.9 a
  I. 0.6
  II. 0.7
  III. 0.8
  IV. 0.9
  V. 1.0
  VI. 1,1
  VII. 1,2
  VIII. 1,3
  IX. 1,4
  X. 1,5
  е д

Задача 10. Стальная стойка длиной l сжимается силой F. Требуется: 1) найти размеры поперечного сечения при расчётном сопротивлении на простое сжатие R = 200 МПа (расчет производить последовательными приближениями, предварительно задавшись коэффициентом j=0,5); 2) найти значение критической силы и коэффициент запаса устойчивости. Данные взять из табл. 10.

Задача 11. На двутавровую балку, свободно лежащую на двух жестких опорах (рис. 10), с высоты h падает груз Q. Требуется: 1) найти наибольшее нормальное напряжение в балке; 2) решить аналогичную задачу при условии, что правая опора заменена пружиной, податливость которой (т. е. осадка от груза 1 кН) равна a; 3) сравнить полученные результаты. Данные взять из табл. 11

Указание: При наличии упомянутой в п. 2 пружины Dст=Dб+bDпр, где Dб—прогиб балки, лежащей на жестких опорах, в том сечении, где приложена сила Q (при статическом действии этой силы); Dпр — осадка пружины от реакции, возникающей от силы Q; b — коэффициент, устанавливающий зависимость между осадкой пружины и перемещением точки приложения силы Q, вызванным поворотом всей балки вокруг центра шарнира левой опоры как жесткого целого(коэффициент b находят из подобия треугольников).

Рисунок 10 – Схемы балок

 
 
 


Таблица 11

№ строки Схема по рис.10 № двутавра l, м Q, Н h, см 103 a, м/кН
  I.   2,1      
  II. 20а 2,2      
  III.   2,3      
  IV. 24а 2,4      
  V.   2,5      
  VI. 27а 2,6      
  VII.   2,7      
  VIII. 30а 2,8      
  IX.   2,9      
  X.   3,0      
  е д е г д е

 

 


Учебное издание

 

 

Составители: Соловей Павел Иванович

 

Хвисевич Виталий Михайлович

 

Менеджмент и управление: сущность и проблематика

 

Понятие «менеджмент» является многозначным. С одной стороны, менеджмент особое искусство, которое заключается в умении так регулировать действия людей, чтобы они не замечали над собой давления или насилия. С другой стороны, это процесс, направленный на достижение целей организации посредством упорядочения преобразований ресурсов в требуемые результаты (изделия, услуги).

Менеджмент можно также рассматривать как науку, как систему принципов, методов и технологий управления. В то же время сложность социально-технических организаций, подвижность и изменчивость внешней среды позволяют рассматривать менеджмент как искусство.

Менеджментом также называют практическую деятельность человека.

И в зависимости от специфики объекта управления выделяют социальный,

инвестиционный, финансовый, стратегический и прочие виды менеджмента.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)