 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Канонические уравнения метода сил
На плоскую стержневую систему с известными геометрическими размерами и заданной топологией (рис. 16.9,а) независимо друг от друга действуют р вариантов силовых полей (постоянная и временные нагрузки). Будем считать, что в состав постоянной и временных нагрузок входят сосредоточенные силы и моменты, а также распределённые на различных участках нагрузки с заданными законами изменения интенсивностей, в том числе и равномерно распределённые нагрузки. Изменение жесткостных характеристик поперечных сечений вдоль осей элементов сооружения на изгиб EJk, сдвиг GAk и растяжение–сжатие EАk примем по ступенчато переменному закону.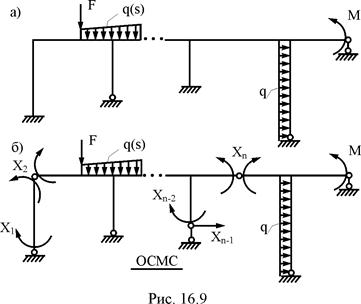 
Степень статической неопределимости заданного сооружения равна n, т.е. сооружение имеет n лишних связей. Образуем геометрически неизменяемую статически определимую основную систему метода сил (ОСМС), удалив из расчётной схемы сооружения n лишних связей (рис. 16.9,б). Действие отброшенных связей заменим соответствующими реакциями X1, X2,..., Xj, …, Xn. Эти реакции в дальнейшем будем называть неизвестными метода сил. В п. 16.1 уже упоминалось о том, что при известных значениях усилий в лишних связях X1, X2,..., Xj, …, Xn задача расчёта заданного сооружения сводится к расчёту статически определимого сооружения, каким является основная система метода сил. Неизвестные метода сил X1, X2,..., Xj, …, Xn определим из условия эквивалентности напряжённо-деформированных состояний заданного сооружения (рис. 16.9,а) и его основной системы метода сил (рис. 16.9,б), т.е. из условия равенства нулю перемещений по направлению Xi (i = 1, 2, …, n)в основной системе метода сил от заданной нагрузки и неизвестных метода сил X1, X2,..., Xj, …, Xn:
D1 = 0, D2 = 0, …, Di = 0, …, Dn = 0. (16.1)
Каждое из перемещений в соотношении (16.1) в соответствии с принципом независимости действия сил представим как сумму перемещений отдельно от каждого неизвестного метода сил X1, X2,..., Xj, …, Xn и заданной нагрузки:
………………………………………………………… (16.2)
…………………………………………………………
В i-й строке выражений (16.2) записаны перемещения по направлению усилия Xi в основной системе метода сил, а именно: 
– от неизвестного метода сил X1; 
– от неизвестного X2; 
– от Xi;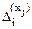 
– от Xj; 
– от Xn; DiF – от заданной нагрузки. Каждое из упомянутых перемещений представим, повторно пользуясь принципом независимости действия сил, в виде:
,
,
………………
, (16.3)
………………
,
………………
.
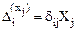Из формул (16.3) следует смысл коэффициентов dii и dij: dii – перемещение по направлению усилия Xi от Xi = 1, dij – перемещение по направлению усилия Xi от Xj = 1 в основной системе метода сил.
После подстановки соотношений (16.3) в выражения (16.2) получим систему канонических уравнений метода сил:
(16.4)
В системе уравнений (16.4) коэффициенты при неизвестных dii, расположенные на главной диагонали, называются главными коэффициентами, коэффициенты dij – побочными. Свободные члены системы канонических уравнений DiF при силовом воздействии называются грузовыми коэффициентами. Побочные коэффициенты dij и dji подчиняются теореме о взаимности перемещений (см.7 лекцию), т.е.dij = dji.
Определив коэффициенты при неизвестных и свободные члены системы канонических уравнений и решив её, получим неизвестные метода сил X1, X2,..., Xj, …, Xn, т.е. усилия в лишних связях.
Поиск по сайту: