Законов ВЛАСТИ

Пусть на пути сферич. фронта свет. волны распол. круглый непрозрачный диск, к-й закрыв. 1-е m зон Френеля.

A= A_m+1-A_m+2+A_m+3-A_m+4+…=A_m+1/2+(A_m+1/2-A_m+2+ A_m+3/2)+(A_m+3/2-…=A_m+1/2

Видно что в т.P всегда наблюд. max. Расчитаем радиус зон Френеля.

r_m²=a²-(a-h)²=(b-ml/2)²-(b+h)², пренебрегая величинами порядка l² окончательно получаем

r_m=Ö(abml/(a+b) сферический фронт свет. волны

r_m=lim_a®¥Ö(abml/(a+b))=Ö(bml) -плоский фронт свет. волны.

2. Решение уравнения Шредингера для водородоподобных атомов. Пространственное распределение электрона в атоме водорода.

Рассмотрим систему, состоящую из неподвижного ядра зарядом +z и 1-го электрона, находящегося около ядра (атом водорода или водородоподобная система). Потенциальная функция U(r)=-ze(c. 2)/4πε₀r(c.2). Стационарное уравнение Шредингера для этого случая имеет вид Dψ+ (2m/ħ(c.2))*(E+(1/4πε₀)*(ze(c.2)/r(c.2))*ψ=0. Для решения этого уравнения удобно перейти к сферическим координатам: ψ(x,y,z)=ψ(r,θ,φ). Расчёты показывают, что это уравнение Шредингера имеет решение при любом E>0(электрон вне атома). И при E<0, удовлетворяющие условию: E_n=-(1/4πε₀)*(mz(c.2)e(c.4)/2ħ(c.2))*(1/n(с.2)). Решение уравнения Шредингера удобно искать в виде ψ(r,θ,φ)=R(r)θ(θ)Ф(φ), т.е. представим волновую функцию в виде произведения 3-х функций, каждая из кот-х зависит только от 1 переменной. R(r)-радиальная функция распределения; θ(θ) и Ф(φ) – функции углового распределения. В зависимости от значения орбитального квантового числа L=0,1,2,3,… состояние электрона в атоме обозначают s,p,d,f. Для электрона 1s-состоянии(n=1,L=0) функция радиального распределения R(r) имеет вид:

Максимум этой функции приходится на r=0,529Å, т.е. совпадает с 1-м боровским радиусом. Функция углового распределения для 1s состояния:

Для электронов p-состояний функция углового распределения имеет вид в зависимости от значения магнитного квантового числа:

Видно, что современным представлениям соответствуют не орбиты, по кот-м движется электрон в атоме, а некоторая совокупность положений электронов в атоме(электронное облако, форма кот-го определяется значением квантовых чисел m, n, L, поэтому вместо термина орбита используют термин орбиталь. Каждой орбитали соответствует своё состояние электрона в вакууме, описанное волновой функцией.

M_z=mħ

p-состояние: L=1;m=0,±1

Видно, что положение вектора М в пространстве квантуется. Он может принимать только определённое положение в пространстве. Энергия электрона в атоме зависит от главного квантового числа n. Однако, при данном значении n, кроме n=1, значение L и m могут быть разными. Это значит, что одному и тому же уровню энергии E_n(собственное значение энергии) соответствует несколько различных состояний, каждое из которых описано своей волновой функцией. Состояния с одинаковыми энергиями наз-ся вырожденными. Число состояний, обладающих данным значением энергии E_n наз-ся кратностью вырождения. Кратность вырождения можно сосчитать по формуле: Σ[L=0, n-1] (2L+1)=2*n(c.2).

3. Закон радиоактивного распада. Правила смещения для α- и β-распадов.

Отдельные радиоактивные ядра испытывают распад независимо друг от друга, поэтому количество распавшихся ядер dN за время dt пропорционально числу имеющихся ядер N и времени-(1),где λ- постоянная распада, характерная величина для данного вещества. Знак минус указываот на убыль радиоактивных ядер. Из (1) находим уравнение (закон) радиоактивного распада, где N₀- начальное количество ядер, N - количество нераспавщихся ядер к моменту времени t.

Время, за которое распадается половина первоначального количества ядер, называется периодом полураспада Т _. Т.к. активность распада ядра носит случайный характер, то постоянная распада λ характеризует вероятность распада. Обратная же ей величина называется средним временем жизни радиоактивного ядра:

Радиоактивные вещества характеризуются активностью, равную числу ядер, распадающиеся за 1 с: За единицу активности принят 1Бк (беккерелях) = 1распад/с. Часто пользуются внесистемной единицей I Кю (кюри) равно3,7*10¹⁰ расп/с. Активность радиоактивного вещества массой m равна где N_A – число Авогадро, А – атомная масса. Правила смещения для α и β-распадов:

^A_ZX-> ^A-4_Z-2Y+ ⁴₂α (Заряд ядра уменьшается на две единицы, а массовое число на 4.)

^A_ZX-> ^A_Z+1Y+ ⁰_-1e (Из материнского ядра образуется дочернее ядро, расположенное на одно место правее в табл Менд-ва).

Билет №19

1. Дифракция рентгеновских лучей. Формула Вульфа-Брейта.

В изучении строения электронных оболочек большую роль сыграли рентгеновские лучи, открытые Рентгеном. Эти лучи возникают при прямом взаимодействии летящих с катода электронов с атомами материала анода. Для их получения используются специальные рентгеновские трубки, в которых между катодом и анодом создается напряжение. Рентгеновские лучи представляют собой короткие электромагнитные волны. Волновая электромагнитная природа этих лучей была доказана опытами по дифракции электронов на кристаллах, проделанных Лауэ с сотрудниками. Кристалл, состояния из упорядочение расположенных частиц, представляет собой пространственную дифракционную решетку, дифракцию рентгеновских лучей можно рассматривать как результат их отражения от системы параллельных атомных, плоскостей, Для того, чтобы лучи, отраженные от соседних плоскостей, усиливали друг друга, необходимо, чтобы разность хода между ними была равна целому числу волн (интерференционные максимумы), те Δ=АВ+ВС=2dsinj=kl => максимумы интенсивноcтей дифрагирован-ных лучей будут наблюдаться для углов, удовлетворяющих условию 2dsinj=kl.

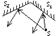Эта формула называется формулой Вульфа-Брэгга. Существует две разновидности рентгеновских лучей, причины возникновения которых совершенно различны. Одна из компонент представляет собой тормозное излучение, имеющая непрерывный спектр.

Возникновение этого излучения можно объяснить так. Вокруг движущегося электрона существует магнитное поле. При ударе об анод происходит резкое изменение скорости электрона и соответственно магнитного поляг в результате чего возникают электромагнитные волны. Сплошной спектр такого излучения объясняется тем, что различное электроны по разному тормозятся атомами анода, что и приводит к излучению различных волн. Согласно квантовой теории часть кинетической энергии электрона переходит при соударении в теплоW, остальная часть в энергию фотона рентгеновского излучения: hn=mu²/2–W. Т.о. с формальной точки зрения возникновение тормозного рентгеновского излучения обратно внешнему фотоэффекту.

2. Колебательные и вращательные спектры молекул. Колебательное и вращательное квантовые числа.

Изменение энергии в молекулах происходит в основном, как и в атоме за счёт изменения электронной конфигурации, образования периферич-й части молекул. Однако, при данной электронной конфигурации ядро в молекуле может колебаться относительно положения равновесия и молекула может вращаться как целое. Этим двум видам движения соответствует колебательная E_υ и вращательная E_вр энергии, которых не может быть у отдельного атома. Эти 2 вида энергии также квантуются. E_υ=(ħw/2)*(υ+1), где υ=0, 1, 2, … - колебательное квантовое число. E_вр=(ħ(с.2)/2I)*(I+1)*J, где I=0, 1, …-момент инерции молекул. J- вращательное квантовое число. Таким образом, энергия молекулы будет складываться из 3-х частей: E= E_e +E_υ +E_вр. Всегда: E_e >E_υ >E_вр. По порядку величины этих энергий можно оценить так: E_e:E_υ:E_вр=1:√m_e/M`: m_e/M. m_e-масса электрона; M-масса молекулы. Переходы только м\у электронными уровнями обуславливают электронными спектрами молекулы, кот-е наблюдаются в видимой и ультрофиолетовой областях спектра. Переходы только м\у колебательными уровнями обуславливают колебательные спектры молекулы, кот-е наблюдаются в инфракрасной области спектра. Переходы только м\у вращательными уровнями обуславливают вращательные спектры молекулы, кот-е наблюдаются в дальней инфракрасной области спектра и микроволновом диапазоне спектра. В общем случае частота излучённого или поглощённого фотона может быть определена по формуле: ▲E=hν,

ν=▲E/h=(▲E_e/h)+(▲E_υ /h)+(▲E_вр/h). Всегда для любой молекулы:

▲E_e >>▲E_υ >>▲E_вр.

3. Ядерные реакции и законы сохранения. Энергия ядерной реакции.

Ядерными реакциями называются превращения атомных ядер, происходящие.в результате их взаимодействия с элементарными частицами или друг с другом. Обычно ядерная реакция вызывается бомбардировкой ядер мишени _ZХ^А потоком ускоренных частиц:α - частиц, протонов, нейтронов и т.д. В результате интенсивного взаимодействия исходного ядра и налетающей частицы, а образуется новое ядро и некоторая частица b,разлетающиеся в различных направлениях. Ядерную реакцию, как и химическую, обычно записывают в виде уравнения.

Экспериментально было установлено, что яд реакции вызываемыми не очень быстрыми частицами проходит в 2 этапа: X+a->П->Y+b

На 1м этапе, в рез-те взаимод-я матер ядра X и элем частицы а образ-ся промеж ядро П (составное ядро). За очень короткое время энергия привнесенная частицей а перераспределяется м/у нуклонами состав ядра П, в рез-те чего оно оказ-ся в возб-м сост-и. На 2м этапе реакции сост ядро П превращается в дочернее ядро Y с одноврем-м испусканием эл част b. Если част а и b тожд-ны, то такой процесс наз-ся рассеянием. Яд реакции, вызыв-емые быстрыми част-ми происходит без образ-я промеж ядра П наз-ся прямыми.

В ядерных реакциях выполняются те же законы сохранения. что и при радиоактивном распаде: законы сохранения энергии, импульса, электрического заряда, количества нуклонов, спина.

Закон сохранения энергии в реакции учитывая, что полная энергия ядер и частиц равна энергии покоя и кинетической энергии будет: ;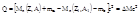

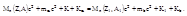
Изменение кинетической энергии в реакции называют энерг ией реакции или тепловым эффектом. Как видно . В эндотермической реакции Q>0 происходит преобразование части энергии покоя ядра мишени и бомбардирующей частицы в кинетическую энергия продуктов реакции. Такая реакция становится возможной; лишь при некоторой минимальной энергии налегающей частицы, которая называется пороговой энергией данной эндотермической реакции:

Билет №20

1. Интерференция света. Когерентные волны. Условия максимумов и минимума. Способы получения когерентных волн.

Явление интерференции света состоит в отсутствии простого суммирования интенсивности волн при их наложении т.е. взаимном усилении волн одних т-к прост-ва и ослабления в др-х.

Устойчивую картину интерференции света дают только когерентные волны. Две волны яв-ся когер-ми если:

4) l₁=l₂ или n₁=n₂

5) Δφ=const

6) Ë₁= Ë₂ (Волны поляризованы в одной пл-ти).

Оптической длиной пути наз. Величина =-я произвед-ю геометр-й длины пути на показатель преломления среды в которой распростр-ся луч света. Оптическая разность хода 2-х лучей D=l₁n₁-l₂n₂. max-м интерф-ии наблюдается если D=2ml/2, (m=0,1,…) min-м если D=(2m+1)l/2, (m=0,1,…).

Способы получения когерентных волн

1)Бипризма Френеля 2)Бизеркала Френеля 3)Билинза Бийе 4)зеркало Ллойда

Когерентными источниками являются мнимые изображенияS1 и S2.Попадая на экран, лучи S1 и S2 создают устойчивую интер-ю картину в виде чередующихся темных и светлых полос.

2. Закономерности в спектре излучения атома водорода. Сериальная формула.

В нормальных условиях атомы не излучают (как и в стационарном состоянии). Чтобы вызвать излучение атомов, надо увеличить их внутренню энергию. Спектры изолированных атомов носят ограниченный характер.

Причем линии в спектре атома, в том числе и атоме водорода, расположены не хаотично, а объединяются в группы, которые называются спектральными сериями. Фор-ла, опред знач-е длины волны в кажд из серии: ν=1/λ=R(1/n² – 1/m²). n=n+1, n+2,.. λ=1,2,3,… (сериальная ф-ла) R=1,092*10м^-1 пост-я Ридберга. В общем случае записывают 1/λ=Rz²(1/n² – 1/m²).

Энергия фотона преш-го с уровня n на m: hv =E_m-E_n=(hz²me⁴/(4πε₀)²2ħ²)(1/n²-1/m²).

Серия Лаймона – ν=1/λ=R(1/1 – 1/n²), n=2,3,4…,в УФ области.

Серия Бальмера – ν=1/λ=R(1/2² – 1/n²), n=3,4,5… видимая область и близкая УФ. Серия Пашена – ν=1/λ=R(1/3² – 1/n²), n=4,5,6…, инфракрасная область. Излучается в видимой и близкой УФ волнах. Все остльные серии лежат в ИК области света.

3. Энергия связи ядра. Удельная энергия связи и ее зависимость от положения элемента в таблице Менделеева.

Масса ядра всегда меньше суммы масс нуклонов, из к-х оно состоит Δm=z*m_p+(A-z)*m_n-m_я - дефект масс. Энергия связи ядра: E_св= Δm*с²= (z*m_p+(A-z)*m_n-m_я)*с²

Удельная энергия связи: E_уд= E_св/A (приходящая на один нуклон).

Размер ядра сост порядка 10^-15м. Из кривой видно, что при делении тяж ядер (уран) появл-ся осколки деления находящиеся в средней части табл Менд. При этом разность отдельных энерг связей в конце и середине при делении выделяются в качестве энергии реакции.

Если перемещ-ся из начала табл Менд в ее середину энерг выход таких реакций будет знач-но больше – реакции термоядерного синтеза.

Билет №21

1. Выведите условие интерференциальных максимумов и минимумов при наложении двух когерентных волн.

Явление интерференции света состоит в отсутствии простого суммирования интенсивности волн при их наложении т.е. взаимном усилении волн одних т-к прост-ва и ослабления в др-х.

Устойчивую картину интерференции света дают только когерентные волны. Две волны яв-ся когер-ми если:

1. l₁=l₂ или n₁=n₂

2. Δφ=const

3. Ë₁= Ë₂ (Волны поляризованы в одной пл-ти).

Оптической длиной пути наз. Величина =-я произвед-ю геометр-й длины пути на показатель преломления среды в которой распростр-ся луч света. Оптическая разность хода 2-х лучей D=l₁n₁-l₂n₂. max-м интерф-ии наблюдается если D=2ml/2, (m=0,1,…) min-м если D=(2m+1)l/2, (m=0,1,…).

Рассмотрим 2 когер-е волны, к-е налагаются др. на др. возбуждают в нек-й т-ке прост-ва результир-е кол-я.

A²=a₁²+a₂²+2√(a₁a₂)cosd, d=a₂-a₁ m=0,1,…

Ë₁(r,t)=A₁cos(wt+kr₁+a₁), Ë₂(r,t)=A₂cos(wt+kr₂+a₂).

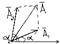Наиболее отчетливая интерф-я картина наблюлается когда A₁= A₂.

I=I₁+ I₂+2√(I₁ I₂)cosd.

Если налаг. волны не когерен. То 2-е условие не выполняется и угол d будет менятся со временем т.к. всякий фотоприемник обладает инерционностью то он будет усреднять значение интенсивности, среднее значение <cosd>=0 т.к. 0<=d<=p то I=I₁+ I₂= 2I₁ т.е. в случае некогерентных волн происходит простое суммирование интенсивности. Если волны когерентны то D=const и в зависимости от значения этого угла -1<cosd<1 след-но при наложении когер-х волн I_max=4I₁, I_min=0 (A₁= A₂). Обычные источники света дают не когерентное излучение.

2. Объясните возникновение потенциального барьера на границе полупроводников p- и n-типа.

P-n переход представляет из себя тонкий слой на границе м/у 2мя областями одного и того же кр-ла, отлич-ся типом проводимости. В n-области осн-ми носителями яв-ся эл-ны, а в p-области – дырки.

В области p-n перехода происходит диффузия во встречных направлениях дырок и эл-нов. Эл-ны попадают из n в p-область рекомбинируя с дырками. Дырки перемещаясь из p в n-область рекомбинируют с эл-нами. В рез-те этого p-n перехода оказ-ся сильно обедненной своб носителями заряда и поэтому имеет большое электрич сопротив-е. Одновременно на границе p-n областей возникает двойной электрич слой, образ отриц ионами акцепторной примеси в p-области, и полож ионами донорной примеси в n-области. При нек-й концентрации ионов в двойном эл слое наступает равновесие. С т зр зонной теории, равновесие наст-ет тогда, когда срав-ся уровни Ферми p и n областей. Изгибание электрич зон в области p-n перехода обусловлено тем, что потенц энергия эл-нов p области больше, чем в n и соответственно дырок n>p области.

3. Соотношение неопределенностей Гейзенберга. Применяя соотношение неопределенностей показать, что для движущейся частицы, неопределенность координаты, которой равна длине волны де-Бройля, неопределенность скорости равна самой скорости.

Во всех макроскопических системах электрон ведет себя как частица, локализованная в малом объеме, обладающая определенной координатой и скоростью. При движении электрона в атоме проявляются его волновые свойства в большей степени, как и во всех микроскопических частицах, но волна не локализована в пространстве, а безгранична.

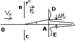Пусть электроны движутся в направлении ОА со скоростью Vx и встречают узкую щель ВС с шириной а. DE – экран, на который будут попадать электроны. Т.к. электроны обладают волновыми свойствами, то при прохождении через узкую щель они дифрагируют, в результате чего электроны будут попадать не только в точки экрана DE, расположенные непосредственно за щелью, но распределяется по всему экрану. Представим, что электрон – классическая частица. Она характеризуется координатой и количеством движения. Можно охарактеризовать координату электрона в момент прохождения щели как координату щели. В таком определении координаты, однако, есть неточность, обусловленная шириной щели. Обозначим эту неопределенность через ∆x=a. После прохождения щели составляющая импульса Px≠0, т.к. вследствии дифракции изменяется скоростью. Составляющая импульса электрона не может быть определено точно, а лишь с некоторой погрешностью ∆Px≥Psinφ1=Pλ/a=hλ/λa=h/a; ∆Px*∆x≥h (1) – соотношение неопределенностей Гейзенберга.

законов ВЛАСТИ

Предисловие

ЗАКОН 1

НИКОГДА НЕ ЗАТМЕВАЙ ГОСПОДИНА

ЗАКОН 2

НЕ ДОВЕРЯЙ ДРУЗЬЯМ БЕЗГРАНИЧНО, НАУЧИСЬ ИСПОЛЬЗОВАТЬ ВРАГОВ

ЗАКОН 3

СКРЫВАЙ СВОИ НАМЕРЕНИЯ

ЗАКОН 4

ВСЕГДА ГОВОРИ МЕНЬШЕ, ЧЕМ КАЖЕТСЯ НЕОБХОДИМЫМ

ЗАКОН 5

ОЧЕНЬ МНОГОЕ ЗАВИСИТ ОТ РЕПУТАЦИИ - БЕРЕГИ ЕЕ ЦЕНОЙ ЖИЗНИ

ЗАКОН 6

ЗАВОЕВЫВАЙ ВНИМАНИЕ ЛЮБОЙ ЦЕНОЙ

ЗАКОН 7

ЗАСТАВЬ ДРУГИХ РАБОТАТЬ НА СЕБЯ И ПОЛЬЗУЙСЯ РЕЗУЛЬТАТАМИ

ЗАКОН 8

ВЫНУЖДАЙ ЛЮДЕЙ ПОДОЙТИ К СЕБЕ, ЕСЛИ НУЖНО, ИСПОЛЬЗУЙ ПРИМАНКУ

ЗАКОН 9

ДОБИВАЙСЯ ПОБЕДЫ ДЕЙСТВИЯМИ, А НЕ ДОВОДАМИ

ЗАКОН 10

ИНФЕКЦИЯ: ИЗБЕГАЙ НЕВЕСЕЛЫХ И НЕВЕЗУЧИХ

ЗАКОН Петр.

СТАРАЙСЯ, ЧТОБЫ ЛЮДИ ЗАВИСЕЛИ ОТ ТЕБЯ

ЗАКОН 12

ПРОЯВЛЯЙ ИНОГДА ЧЕСТНОСТЬ И ЩЕДРОСТЬ, ЧТОБЫ ОБЕЗОРУЖИТЬ СВОЮ ЖЕРТВУ

ЗАКОН 13

ПОПРОСИВ О ПОМОЩИ, ВЗЫВАЙ К СВОЕКОРЫСТИЮ ЛЮДЕЙ И НИКОГДА - К ИХ МИЛОСТИ ИЛИ ВЕЛИКОДУШИЮ

ЗАКОН 14

ИГРАЙ РОЛЬ ДРУГА, ДЕЙСТВУЙ, КАК ШПИОН

ЗАКОН 15

РАЗБЕЙ ВРАГА ПОЛНОСТЬЮ

ЗАКОН 16

ИСПОЛЬЗУЙ СВОЕ ОТСУТСТВИЕ, ЧТОБЫ ПРЕУМНОЖИТЬ УВАЖЕНИЕ И ЧЕСТЬ

ЗАКОН 17

ДЕРЖИ ДРУГИХ В ПОДВЕШЕННОМ СОСТОЯНИИ: ПОДДЕРЖИВАЙ АТМОСФЕРУ НЕПРЕДСКАЗУЕМОСТИ

ЗАКОН 18

НЕ СТЮЙ КРЕПОСТЕЙ, ЧТОБЫ ЗАЩИТИТЬ СЕБЯ: ИЗОЛЯЦИЯ ОПАСНА

ЗАКОН 19

ЗНАЙ, С КЕМ ИМЕЕШЬ ДЕЛО: НЕ НАНОСИ ОБИДУ КОМУ НЕ СЛЕДУЕТ

ЗАКОН 20

НИ С КЕМ НЕ ОБЪЕДИНЯЙСЯ

ЗАКОН 21

ПРИКИНЬСЯ ПРОСТАКОМ, ЧТОБЫ НАДУТЬ ПРОСТАКА: КАЖИСЬ ГЛУПЕЕ СВОЕЙ МИШЕНИ

ЗАКОН 11

ИСПОЛЬЗУЙ ТАКТИКУ КАПИТУЛЯЦИИ: ОБРАТИ СЛАБОСТИ В СИЛУ

ЗАКОН 23

КОНЦЕНТРИРУЙ СВОИ СИЛЫ

ЗАКОН 14

ПОСТУПАЙ КАК ИСТИННЫЙ ПРИДВОРНЫЙ

ЗАКОН 25

СОТВОРИ СЕБЯ ЗАНОВО

ЗАКОН 26

ДЕРЖИ РУКИ ЧИСТЫМИ

ЗАКОН 27

ИГРАЙ НА НУЖДАХ ЛЮДЕЙ, СОЗДАВАЯ АРМИЮ ФАНАТИЧНЫХ ПРИВЕРЖЕНЦЕВ

ЗАКОН 28

ПРИСТУПАЙ К ДЕЛУ БЕЗ КОЛЕБАНИЙ

ЗАКОН 29

ПЛАНИРУЙ ВСЕ ДО САМОГО КОНЦА

ЗАКОН 30

ДОБИВАЯСЬ УСПЕХА, НЕ ПОКАЗЫВАЙ УСИЛИЙ

ЗАКОН 31

КОНТРОЛИРУЙ ВСЕ ВАРИАНТЫ: ПУСТЬ ДРУГИЕ ИГРАЮТ КАРТАМИ, КОТОРЫЕ СДАЕШЬ ТЫ

ЗАКОН 32

ИГРАЙ НА ЛЮДСКИХ ФАНТАЗИЯХ

ЗАКОН 33

ЗНАЙ СЛАБЫЕ СТРУНКИ КАЖДОГО ЧЕЛОВЕКА

ЗАКОН 34

БУДЬ ЦАРСТВЕННЫМ НА СВОЙ МАНЕР: ВЕДИ СЕБЯ КАК КОРОЛЬ - И БУДЕШЬ ПРИНЯТ КАК КОРОЛЬ

ЗАКОН 35

ОВЛАДЕЙ ИСКУССТВОМ УПРАВЛЕНИЯ ВРЕМЕНЕМ

ЗАКОН 36

ПРЕЗИРАЙ ТО, ЧЕМ НЕ МОЖЕШЬ ОБЛАДАТЬ: ИГНОРИЮВАНИЕ - ЛУЧШАЯ МЕСТЬ

ЗАКОН 37

СОЗДАВАЙ НЕЗАБЫВАЕМЫЕ ЗРЕЛИЩА

ЗАКОН 38

ДУМАЙ ЧТО ХОЧЕШЬ, НО ДЕЙСТВУЙ КАК ВСЕ

ЗАКОН 39

МУТИ ВОДУ, ЧТОБЫ ПОЙМАТЬ РЫБКУ

ЗАКОН 40

С ПРЕЗРЕНИЕМ ОТВЕРГАЙ БЕСПЛАТНЫЕ ОБЕДЫ

ЗАКОН 41

СТАРАЙСЯ НЕ ИДТИ ПО СТОПАМ ВЕЛИКИХ

ЗАКОН 42

ПОРАЗИ ПАСТЫРЯ - И ПАСТВА РАССЕЕТСЯ

ЗАКОН 43

ЗАВОЕВЫВАЙ СЕРДЦА И УМЫ ОКРУЖАЮЩИХ

ЗАКОН 44

ОБЕЗОРУЖИВАЙ И ПРИВОДИ В ЯЮСТЬ С ПОМОЩЬЮ ЭФФЕКТА ЗЕРКАЛА

ЗАКОН 45

ПРОПОВЕДУЙ НЕОБХОДИМОСТЬ ПЕРЕМЕН, НО НЕ СЛИШКОМ

УВЛЕКАЙСЯ РЕФОРМАМИ

ЗАКОН 46

НИ В КОЕМ СЛУЧАЕ НЕ КАЖИСЬ СЛИШКОМ СОВЕРШЕННЫМ

ЗАКОН 47

НЕ ЗАХОДИ ДАЛЬШЕ НАМЕЧЕННОЙ ЦЕЛИ; ПОБЕЖДАЯ, ЗНАЙ, КОГДА ОСТАНОВИТЬСЯ

ЗАКОН 48

ОБРЕТИ НЕОПРЕДЕЛЕННОСТЬ ФОРМЫ

Поиск по сайту: