 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задача 10. Определить, что являлось элементной базой ЭВМ 2-го поколения?
Определить, что являлось элементной базой ЭВМ 2-го поколения?
Ответ: транзисторы
§3. Системы счисления
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит систем счисления состоит из символов, которые называются цифрами. Например, в десятичной системе счисления числа записываются с помощью десяти известных цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Все системы счисления делятся на две большие группы: позиционную и непозиционную. В позиционной системе счисления значение цифры зависит от её нахождения в позиции числа, а в непозиционных - не зависит.
Самой распространённой из непозиционных систем счисления является римская. В качестве цифр в ней используются латинские буквы: I=1, V=5, X=10, L=50, C=100, D=500, M=1000. Здесь значение цифры не зависит от её позиции в числе. Например, в числе ХХХ=30 цифра Х встречается трижды и в каждом случае обозначает одну и ту же величину - 10, три числа по 10 в сумме дают 30.
Римскую систему счисления из-за её специфических свойств иногда называют полупозиционной: так, в числах IX и XI знак I обозначает в обоих случаях единицу (признак непозиционной системы), но, будучи расположенным слева от знака X (обозначающего десять), вычитается из десяти, а при расположении справа – прибавляется к десяти. В первом случае полное значение числа равно 9, во втором – 11.
Величина числа в римской системе счисления определяется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа- то прибавляется. Например, запись десятичного числа 1998 в римской системе счисления будет выглядеть следующим образом: MCMXCVIII=1000+(1000-100)+(100-10)+5+1+1+1.
Примером позиционной формы записи чисел является та, которой мы пользуемся (так называемая арабская форма чисел). Так, в числах 123 и 321 значения цифры 3, например, определяются ее положением в числе: в первом случае она обозначает три единицы (т.е. просто три), а во втором – три сотни (т.е. триста).
Тогда любое число в системе счисления с основанием p представляется так:
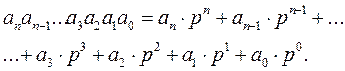 (12)
(12)
| Десятичная система | Двоичная система | Шестнадцатеричная система |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F | ||
Таблица 3.
Здесь a0, a1, a2, … an – цифры системы счисления, набор которых anan-1 … … a3a2a1a0 представляет запись числа, суммирования справа в этой формуле осуществляется по правилам десятичной арифметики, наконец, n – номер позиции, которую занимает та или иная цифра (n = 0, 1, 2, 3 …).
Например, для десятичного (p = 10, набор цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) числа 345 его значение рассчитывается по формуле: 3·102 + 4·101 + 5·100 = 300 + 40 + 5 = 345.
В современной информатике используются несколько систем счисления, например, двоичная, шестнадцатеричная и десятичная.
В двоичной системе счисления для представления числа применяются две цифры: 0 и 1.
В шестнадцатеричной системе счисления используются десятичные цифры от 0 до 9 и буквы латинского алфавита – A, B, C, D, E, F.
В качестве примера, соответствие между первыми несколькими натуральными числами указанных систем счисления представлено в таблице 3.
Для различения систем счисления, в которых представлены числа, в обозначение двоичных и шестнадцатеричных чисел вводят дополнительные реквизиты:
- для двоичных чисел – нижний индекс справа от числа в виде цифры 2 или букв В либо b (binary – двоичный), либо знак B или b справа от числа. Например, 1010002 = 101000b = 101000B = 101000B = 101000b;
- для шестнадцатеричных чисел - нижний индекс справа от числа в виде числа 16 или букв H либо h (hexadecimal – шестнадцатеричный), либо знак H или h справа от числа. Например, 3AB16 = 3ABH = 3ABh = 3ABH = 3ABh.
Перевод чисел из одной системы счисления в другую осуществляют по определенным правилам. Правила различаются в зависимости от формата числа – целое или правильная дробь.
Приведём некоторые из правил перевода чисел из одной системы счисления в другую и обратно.
Вначале рассмотрим перевод из десятичной системы счисления в двоичную и шестнадцатеричную. Для выполнения таких переводов можно следовать следующему пошаговому алгоритму:
а. Исходное целое число делится на основание системы счисления, в которую переводится (на 2 - при переводе в двоичную систему счисления или на 16 - при переводе в шестнадцатеричную); получается частное и остаток;
б. Если полученное частное меньше основания системы счисления, в которую выполняется перевод, процесс деления прекращается, переходят к шагу в, иначе над частным выполняют действия, описанные в шаге а;
в. Все полученные остатки и последнее частное преобразуются в соответствии с таблицей перевода в цифры той системы счисления, в которую выполняется перевод;
г. Формируется результирующее число: его старший разряд – полученное последнее частное, каждый последующий младший разряд образуется из полученных остатков от деления, начиная с последнего и кончая первым.
Таким образом, младший разряд полученного числа – первый остаток от деления, а старший – последнее частное.
Рассмотрим несколько примеров использования этого алгоритма.
Пример 1. Выполнить перевод числа 19 в двоичную систему счисления:

Таким образом, 19 = 100112.
Пример 2. Выполнить перевод числа 19 в шестнадцатеричную систему счисления:
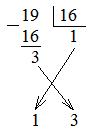
Таким образом, 19 = 1316.
Пример 3. Выполнить перевод числа 123 в шестнадцатеричную систему счисления:
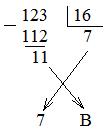
Здесь остаток 11 преобразован в шестнадцатеричную цифру В в соответствии с Таблицей 3 и после этого данная цифра вошла в число. Таким образом, 123 = 7В16.
Теперь рассмотрим пример перевода из двоичной и шестнадцатеричной системы счисления обратно в десятичную. При этом рассчитывается значение числа по приведённой выше формуле (12).
Пример 4. Выполним перевод числа 1316 в десятичную систему счисления.
В соответствие с формулой (1) имеем:
1316 = 1·161 + 3·160 = 16 + 3 = 19.
Таким образом, 1316 = 19.
Пример 5. Выполним перевод числа 100112 в десятичную систему счисления.
В соответствие с формулой (12) имеем:
100112 = 1·24 + 0·23 + 0·22 + 1·21 + 1·20 = 16+0+0+2+1 = 19.
Таким образом, 100112 = 19.
Далее, рассмотрим пример перевода из двоичной системы счисления в шестнадцатеричную. Для этого воспользуемся следующим алгоритмом:
а. Исходное число разбивается на тетрады (т.е. 4 цифры), начиная с младших разрядов, если количество цифр исходного двоичного числа не кратно 4, то оно дополняется слева незначащими нулями до достижения кратности 4;
б. Каждая тетрада заменятся соответствующей шестнадцатеричной цифрой в соответствии с таблицей 3.
Пример 6. Выполним перевод числа 100112 в шестнадцатеричную систему счисления.
Поскольку в исходном двоичном числе количество цифр не кратно 4, дополняем его слева незначащими нулями до достижения числа цифр кратности 4. Теперь имеем:
100112 = 0001 00112.
Здесь: 0011 – первая тетрада (младшая цифра цисла),
0001 – вторая тетрада (старшая цифра числа).
Далее, в соответствии с таблицей 3:
00112 = 112 = 316 и 00012 = 12 = 116.
Тогда 100112 = 1316.
Теперь рассмотрим пример перевода из шестнадцатеричной системы счисления в двоичную. Для этого, воспользуемся следующим алгоритмом:
а. Каждая цифра исходного числа заменяется тетрадой двоичных цифр в соответствии с таблицей 3. Если в таблице 3 двоичное число состоит менее чем из 4-х цифр, оно дополняется слева незначащими нулями до тетрады;
б. Незначащие нули в результирующем числе отбрасываются.
Пример 7. Выполним перевод числа 1316 в двоичную систему счисления.
Из таблицы 3 имеем:
1) 116 = 12 и после дополнения незначащими нулями двоичного числа 12 = 00012;
2) 316 = 112 и после дополнения незначащими нулями двоичного числа 112 = 00112.
Тогда 1316 = 000100112. После удаления незначащих нулей имеем 1316 = 100112.
Теперь рассмотрим некоторые правила перевода правильных дробей. Напомним, что правильная дробь имеет нулевую целую часть, т.е. у нее числитель меньше знаменателя.
Вначале рассмотрим алгоритм перевода правильных дробей из десятичной системы счисления в двоичную и шестнадцатеричную и рассмотрим примеры перевода. Алгоритм перевода имеет следующий вид:
а. Исходная дробь умножается на основание системы счисления, в которую переводится (2 или 16);
б. В полученном произведении целая часть преобразуется в соответствии с таблицей 3 в цифру нужной системы счисления и отбрасывается – она является старшей цифрой получаемой дроби;
в. Оставшаяся дробная часть (это правильная дробь) вновь умножается на нужное основание системы счисления с последующей обработкой полученного произведения в соответствии с шагами а и б;
г. Процедура умножения продолжается до тех пор, пока не будет получен нулевой результат в дробной части произведения или не будет достигнуто требуемое количество цифр в результате;
д. Формируется искомое число так: последовательно отброшенные в шаге б цифры составляют дробную часть результата, причем в порядке уменьшения старшинства.
Пример 8. Выполним перевод числа 0,847 в двоичную систему счисления. Перевод будем выполнять до четырех значащих цифр после запятой.
Имеем:

Таким образом, 0,847 = 0,11012.
В данном примере процедура перевода прервана на четвертом шаге, поскольку получено требуемое число разрядов результата. Очевидно, это привело к потере ряда цифр.
Пример 9. Выполним перевод числа 0,847 в шестнадцатеричную систему счисления. Перевод будем выполнять до трех значащих цифр.
Имеем:

В данном примере также процедура перевода прервана в соответствии с заданным уровнем точности.
Таким образом, 0,847 = 0,D8D16.
Рассмотрим теперь примеры перевода правильных дробей из двоичной и шестнадцатеричной системы счисления в десятичную.
Пример 10. Выполним перевод числа 0,11012 из двоичной системы счисления в десятичную.
Имеем:
0,11012 = 1 · 2-1 + 1 · 2-2 + 0 · 2-3 +1 · 2-4 = 0,5 + 0,25 + 0 + 0,0625 = 0,8125.
Расхождение полученного результата с исходным числом вызвано тем, что процедура перевода в двоичную дробь была прервана.
Таким образом, 0,11012 = 0,8125.
Пример 11. Выполним перевод числа 0,D8D16 из шестнадцатеричной системы счисления в десятичную.
Имеем:
0,D8D16 = 13 · 16-1 + 8 · 16-2 + 13 · 16-3 = 13 · 0,0625 + 8 · 0,003906 + 13 · 0,000244 = 0,84692.
Расхождение полученного результата с исходным числом вызвано тем, что процедура перевода в шестнадцатеричную дробь была прервана.
Таким образом, 0,D8D16 = 0,84692.
Для перевода правильных дробей из двоичной системы счисления в шестнадцатеричную воспользуемся следующим алгоритмом:
а. Исходная дробь делится на тетрады, начиная с позиции десятичной точки вправо, если количество цифр дробной части исходного двоичного числа не кратно 4, оно дополняется справа незначащими нулями до достижения кратности 4;
б. Каждая тетрада заменяется шестнадцатеричной цифрой в соответствии с таблицей 3.
Теперь рассмотрим примеры такого перевода.
Пример 12. Выполним перевод числа 0,11012 из двоичной системы счисления в шестнадцатеричную.
Имеем:
1101 – первая (и единственная) тетрада.
В соответствии с таблице 3 имеем: 11012 = D16.
Тогда 0,11012 = 0,D16.
Пример 13. Выполним перевод числа 0,00101012 из двоичной системы счисления в шестнадцатеричную.
Поскольку количество цифр дробной части не кратно 4, добавим справа незначащий ноль:
0,00101012 = 0,0010 10102
Здесь: 0010 – первая терада, 1010 – вторая тетрада.
В соответствии с таблицей 3: 00102 = 102 = 216 и 10102 = A16.
Тогда 0,00101012 = 0,2A16.
Далее, для перевода правильной дроби из шестнадцатеричной системы счисления в двоичную, воспользуемся следующим алгоритмом и проиллюстрируем его примером:
а. Каждая цифра исходной дроби заменяется тетрадой двоичных цифр в соответствии с таблицей 3.
б. Незначащие нули отбрасываются.
Пример 14. Выполним перевод числа 0,2А16 из шестнадцатеричной системы счисления в двоичную.
По таблице 3 имеем: 216 = 00102 и А16 = 10102.
Тогда 0,2А16 = 0,001010102.
Отбросим в результате незначащий ноль и получим окончательный ответ: 0,2А16 = 0,00101012
В заключение рассмотрим правила перевода неправильных дробей из одной системы счисления в другую. Напомним, что неправильная дробь имеет ненулевую целую часть, т.е. у нее числитель больше знаменателя. При переводе отдельно переводится целая часть числа, отдельно – дробная. Затем полученные результаты складываются. Проиллюстрируем перевод неправильной дроби из одной системы счисления в другую на примере.
Пример 15. Выполним перевод числа 19,847 из десятичной системы счисления в шестнадцатеричную. Перевод будем выполнять до трех значащих цифр после запятой.
Представим исходное число как сумму целого числа и правильной дроби:
19,847 = 19 + 0,847.
Как следует из Примера 2: 19 = 1316, а в соответствии с Примером 9: 0,847 = 0,D8D16.
Тогда имеем:
19 + 0,847 = 1316 + 0,D8D16 = 13,D8D16.
Здесь в правой части использовано правило сложения двух шестнадцатеричных чисел.
Таким образом, 19,847 = 13,D8D16.
§4. Задачи на правила перевода из одной системы счисления в другую
Поиск по сайту: