 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Момент инерции твердых тел
При вращении твердого тела вокруг неподвижной оси ОО (рис. 1) его инерциальные свойства определяются не только массой тела, но и распределением этой массы относительно оси вращения.
Твердое тело, состоящее из материальных точек, каждая массой mi, участвуют во вращательном движении. Мерой инерции каждой материальной точки вращающегося твердого тела является момент инерции Ji. Момент инерции материальной точки относительно неподвижной оси равен произведению массы этой точки на квадрат расстояния ri от точки до оси вращения:
. (2.6)
Рис. 1. Вращение твердого тела массой m вокруг неподвижной оси ОО
Момент инерции твердого тела произвольной геометрической формы относительно неподвижной оси ОО равен алгебраической сумме моментов инерций всех его точек относительно этой оси:
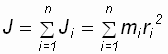, (2.7)
где Ji – момент инерции i- йточки; mi – масса i- й точки; ri – расстояние i- й точки до оси вращения “ОО”.
Для тел правильной геометрической формы моменты инерций описываются точными выражениями. Например: для шара массой m и радиусом r, вращающегося относительно центральной оси, момент инерции J равен произведению 2/5 массы на квадрат радиуса шара (рис. 2):
. (2.8)
Центральной осью вращения ОО (рис. 2) называют ось, проходящую через центр массы тела С.
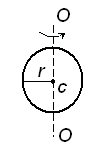
Рис.2. Шар массой m, вращающийся относительно центральной оси ОО. Точка С – центр массы шара
Для сплошного цилиндра массой m момент инерции относительно центральной оси равен произведению 1/2 массы цилиндра на квадрат радиуса основания цилиндра (рис. 3):
. (2.9)
Рис.3. Цилиндр массой m, вращающийся относительно центральной оси “ОО”. Точка С – центр массы цилиндра
При изменении положения оси вращения относительно центра масс изменяется и момент инерции тела. При параллельном переносе оси вращения справедлива теорема Штейнера. По теореме Штейнера определяют момент инерции твердого тела любой геометрической формы относительно нецентральной оси (рис. 4).
Рис. 4. Момент инерции цилиндра относительно центральной оси “11” – J0 и относительно оси “22” – J; b – расстояние между осями
Теорема: “Если ось вращения, проходящую через центр массы тела, переместить параллельно самой себе на расстояние b, то момент инерции относительно этой оси будет равен алгебраической сумме момента инерции тела Jo, относительно центральной оси вращения, и произведению массы тела m на квадрат расстояния b между осями”, то есть
(2.10)
Поиск по сайту: