Связь между линейной и угловой скоростью и ускорением

Отдельные точки вращающегося тела имеют различные линейные скорости v, которые непрерывно изменяют свое направление и зависят от ω и расстояния r соответствующей точке до оси вращения.

Точка, находящаяся на расстоянии r от оси вращения проходит путь Δ S = r Δφ.

Поделим обе части равенства на Δ t:

, при Δ t 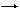0 получим пределы от левой и правой частей равенства:

Но

Таким образом, чем дальше отстоит точка от оси вращения, тем больше ее линейная

скорость. Известно, что

Откуда

Из написанных формул видно, что a _τ, a _n

и a растут с увеличением расстояния точек до оси вращения. Формула v = ω r устанавливает связь между модулями векторов v, r, и ω, которые перпендикулярны друг к другу.

Т.к. ω | r, то можно написать v = ω∙ r ∙ sina это ничто иное как модуль векторного произведения. Таким образом v = [ ω r ]

Рассмотренные простейшие виды движения твердого тела важны потому,

что любое движение твердого тела сводится к ним.

Рассмотрим два последовательных положения тела А₁ и А₂.

Из положения А₁ в положение А₂ тело можно перевести следующим образом: вначале А₁ в А¹ поступательно. Затем из положения А¹ в положение А₂ путем поворота на угол φ вокруг произвольной точки 0.

Следует отметить, что в вращательному движению применимы все формулы кинематики материальной точки с заменой в них линейных величин на соответствующие угловые.

Например:

Поиск по сайту: