МОДЕЛЬ ОЦЕНКИ КАПИТАЛЬНЫХ АКТИВОВ (МОДЕЛЬ ШАРПА)

Ожидаемую доходность актива можно определить с помощью так называемых индексных моделей. Их суть состоит в том, что изменение доходности и цены актива зависит от ряда показателей, характеризующих состояние рынка, или индексов.

Простая индексная модель предложена У. Шарпом в середине 60-х гг. Ее часто называют рыночной моделью. В модели Шарпа представлена зависимость между ожидаемой доходностью

актива и ожидаемой доходностью рынка. Она предполагается линейной- Уравнение модели имеет следующий вид:

где Е(ri) — ожидаемая доходность актива;

у, — доходность актива в отсутствие воздействия на него рыночных факторов;

— коэффициент актива;

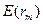— ожидаемая доходность рыночного портфеля;

еi- — независимая случайная (переменная) ошибка. Независимая случайная ошибка показывает специфический риск актива, который нельзя объяснить действием рыночных сил. Значение ее средней величины равно нулю. Она имеет постоянную дисперсию ковариацию с доходностью рынка, равную нулю; ковариацию с нерыночным компонентом доходности других активов, равную нулю.

Приведенное уравнение является уравнением регрессии. Если его применить к широко диверсифицированному портфелю, то значения случайных переменных (еi) в силу того, что они изменяются как в положительном, так и отрицательном направлении, гасят друг друга, и величина случайной переменной для портфеля в целом стремится к нулю. Поэтому для широко диверсифицированного портфеля специфическим риском можно пренебречь. Тогда модель Шарпа принимает следующий вид:

где — ожидаемая доходность портфеля; портфеля;

Yp— доходность портфеля в отсутствие воздействия на него рыночных факторов.

Поиск по сайту: