АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Тема 1.1. Пределы, их свойства

Читайте также:
  1. III. Психические свойства личности – типичные для данного человека особенности его психики, особенности реализации его психических процессов.
  2. Алгебраические свойства векторного произведения
  3. АЛГОРИТМ И ЕГО СВОЙСТВА
  4. Аллювиальные отложения и их свойства
  5. АТМОСФЕРА И ЕЕ СВОЙСТВА
  6. Атрибуты и свойства материи
  7. БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВА
  8. Биосинтез белка и нуклеиновых кислот. Матричный характер реакций биосинтеза. Генетическая информация в клетке. Гены, генетический код и его свойства
  9. Валентные свойства атомов
  10. Валериана лекарственная - лечебные свойства, рецепты
  11. Виды подшипников качения и их свойства
  12. Виды темперамента и соответствующие им психические свойства человека

Практическая работа № 1 «Вычисление пределов»:

Учебная цель: вычислить пределы функций.

Учебные задачи: научится вычислять различные пределы.

 

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

уметь:

· вычислять пределы функций в точке, раскрывать неопределенности

знать:

· основные понятия и методы и методы математического анализа

 

Задачи практической работы:

 

1. Повторить теоретический материал по теме практической работы.

2. Ответить на вопросы для закрепления теоретического материала.

3. Решить вариант.

4. Оформить отчёт

 

 

Обеспеченность занятия (средства обучения):

1. Тетрадь для практических работ (обычная, в клетку).

2. Карточки-задания (25 штук).

3. Калькулятор (простой).

4. Ручка.

Краткие теоретические и учебно-методические материалы по теме практической работы:

Определение предела. Число b – предел функции f(x) при x стремящемся к a, если для каждого положительного числа можно указать такое положительной число 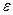, что для всех x, отличных от a и удовлетворяющих неравенству | x-a |< , имеет место неравенство |f(x)-b|<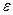

Обозначение предела. Если b есть предел функции f(x) при x стремящемся к a, то записывают это так:

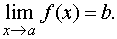
Определение непрерывной функции. Функция f(x) непрерывна в точке a, если

Вычисление пределов функций основано на применении следующих основных теорем:

ТЕОРЕМА 1. Предел суммы двух функций при x стремящемся к a равен сумме пределов этих функций, то есть

ТЕОРЕМА 2. Предел произведения двух функций при x стремящемся к a равен произведению пределов этих функций, то есть

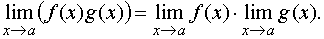
ТЕОРЕМА 3. Предел частного двух функций при x стремящемся к a равен частному пределов, если предел знаменателя отличен от нуля, то есть

и равен плюс (минус) бесконечности, если предел знаменателя 0, а предел числителя конечен и отличен от нуля.


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)