Пример 1

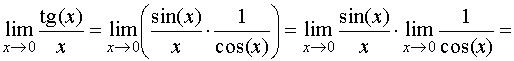
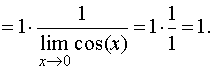
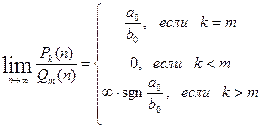
Пример.. Найти пределы:

а) б) , в)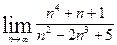

Решение.

а)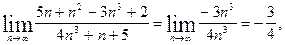

б) ,

в) .

Следует отметить, что формулы (1.5) и (1.6) справедливы не только для многочленов целой степени, но и для многочленов дробной степени, так как для любого a >0.

Пример. Найти пределы.

а) , б) , в) ,

Решение:

а) В числителе три слагаемых соответственно степени: Следовательно, степень числителя равна , а главный член в числителе равен . Аналогично, главный член в знаменателе Имеем по формулам (1.5) и (1.6):

а)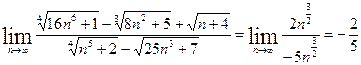

б)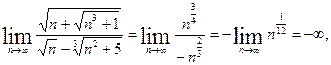

в)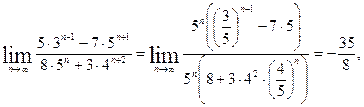

т.к.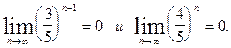

Здесь также можно было использовать идею, что главный член это старший член. Имеем:

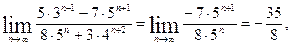
Пример 1.4. (Неопределенности )

а) , б)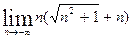

Решение. Для избавления от неопределенности 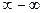здесь следует избавиться от иррациональности в числителе, умножив и разделив данное выражение на соответствующее сопряженное выражение.

а) Используем формулу

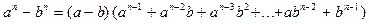
Для данного примера

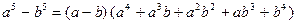
Имеем:

а)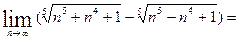

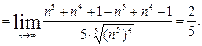
б) Напоминаем, что и при .

Имеем:

= .

Вопросы для закрепления теоретического материала к практической работе.

1. Что такое предел функции?
2. Какая функция называется непрерывной?
3. Основные теоремы для вычисления пределов функций.
4. Замечательные пределы.

Поиск по сайту: