АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Пример 2. Комментарий. На первом шаге была применена теорема о пределе частного, так как предел знаменателя не равен нулю

Читайте также:
  1. X. примерный перечень вопросов к итоговой аттестации
  2. В некоторых странах, например в США, президента заменяет вице-
  3. В примере
  4. Вания. Одной из таких областей является, например, регулирова-
  5. Вашим сообщениям, например, спеть «С днем рождения»
  6. Виды знания. Контрпример стандартному пониманию знания
  7. Власть примера. Влияние с помощью харизмы
  8. Внешний долг (внешняя задолженность): пример России
  9. Вопрос 11. Герои романтических поэм М. Ю. Лермонтова (на примере одного произведения).
  10. Вопрос 2 Проверка и оценка в задачах со случайными процессами на примере решения задач экозащиты, безопасности и риска.
  11. Вопрос 8. Герои романтических поэм А. С. Пушкина (на примере одного произведения).
  12. Второй пример абстрактного синтеза

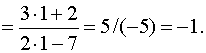
Комментарий. На первом шаге была применена теорема о пределе частного, так как предел знаменателя не равен нулю. На втором шаге использовалась теорема о пределе суммы для числителя и знаменателя дроби. После была применена теорема о пределе произведения.

Пример 3. Найти предел

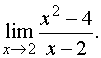
Знаменатель и числитель дроби при x стремящемся к 2 стремятся к нулю, поэтому теорема о пределе частного здесь неприменима. В таких случаях нужно попытаться упростить дробь. Имеем

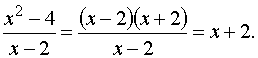
Это преобразование справедливо при всех значениях x, отличных от 2, поэтому в соответствии с определением предела можем написать

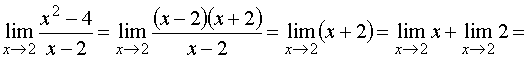
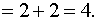
ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ С ПОМОЩЬЮ ТЕОРЕМЫ О ПЕРВОМ ЗАМЕЧАТЕЛЬНОМ ПРЕДЕЛЕ


1 | 2 | 3 | 4 | 5 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)