 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Контрольная работа по Теории вероятностей
Вариант 1. Случайная величина задана распределением:

| |||

| 0,3 | ? | 0,2 |
Найти вероятность для значения х=2, математическое ожидание и дисперсию случайной величины.
Вариант 2. Случайная величина задана распределением:

| |||

| 0,6 | 0,3 | ? |
Найти вероятность для значения х=2, математическое ожидание и дисперсию случайной величины.
Вариант 3. Случайная величина задана распределением:

| -1 | ||

| 0,3 | ? | 0,1 |
Найти вероятность для значения х=1, математическое ожидание и дисперсию случайной величины.
Вариант 4. Случайная величина задана распределением:

| -2 | ||

| 0,4 | 0,3 | ? |
Найти вероятность для значения х=2, математическое ожидание и дисперсию случайной величины.
Вариант 5. Случайная величина задана распределением:

| -1 | ||

| 0,5 | 0,2 | ? |
Найти вероятность для значения х=1, математическое ожидание и дисперсию случайной величины.
Вариант 6. Случайная величина задана распределением:

| -3 | -2 | -1 |

| 0,1 | ? | 0,6 |
Найти вероятность для значения х=-2, математическое ожидание и дисперсию случайной величины.
Вариант 7. Случайная величина задана распределением:

| |||

| 0,15 | 0,35 | ? |
Найти вероятность для значения х=6, математическое ожидание и дисперсию случайной величины.
Вариант 8. Случайная величина задана распределением:

| -1 | -2 | -3 |

| 0,25 | ? | 0,25 |
Найти вероятность для значения х=-2, математическое ожидание и дисперсию случайной величины.
Вариант 9. Случайная величина задана распределением:

| |||

| 0,4 | 0,4 | ? |
Найти вероятность для значения х=4, математическое ожидание и дисперсию случайной величины.
Вариант 10. Случайная величина задана распределением:

| |||

| ? | 0,5 | 0,2 |
Найти вероятность для значения х=2, математическое ожидание и дисперсию случайной величины.
Контрольная работа по Теории вероятностей
Номер варианта определяется по последней цифре личного дела студента, который совпадает с номером его зачетной книжки и студенческого билета. Замечание: если номер зачетной книжки оканчивается цифрой 0, то ваш вариант 10.
Каждая контрольная работа содержит набор заданий, при выполнении которых необходимо соблюдать следующие правила:
1. Работа должна быть выполнена в школьной тетради (12 или 18 листов).
2. Перед решением каждой задачи нужно привести полностью её условие.
3. Следует придерживаться той последовательности при решении задач, в которой они даны в задании, строго сохраняя при этом нумерацию примеров (задач).
4. Не допускается замена контрольного задания другими.
5. Решение задач должны сопровождаться развернутыми пояснениями, нужно привести в общем виде используемые формулы с объяснением употребляемых обозначений, а окончательный ответ следует выделить.
6. На обложке тетради следует написать следующие данные: контрольная работа, по какой дисциплине, фамилию, имя, отчество (полностью), специальность, курс, номер личного дела, вариант, фамилию преподавателя.
При решении контрольных работ следует использовать свои лекции и дополнительную литературу:
1) Белько И.В. Высшая математика для экономистов. III семестр: Экспресс – курс / И.В. Белько, К.К. Кузьмич. – М.: Новое знание, 2002. – 144 с.
2) Емельянов Г.В., Скитович В.П. Задачник по теории вероятностей и математической статистике: Учебное пособие. 2-е изд., стер. – СПб.: Издательство «Лань», 2007. – 336 с.
3)Владимирский Б.М., Горстко А.Б., Ерусалимский Я.М. Математика. Общий курс. – Спб.: Издательство «Лань», 2002. – 960 с. – (Учебники для вузов. Специальная литература).
4) Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика: Учебник.
5) Сборник задач по высшей математике для экономистов: Учеб. пособие / Под ред. В.И.Ермакова. – 2-е изд., испр. – М.: ИНФРА-М, 2008. – 575 с.
6) Вентцель Е.С. Теория вероятностей: Учебник для студ. вузов/ Елена Сергеевна Вентцель. – 9-е изд., стер. – М.: Издательский центр «Академия», 2003. – 576 с.
7) Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов / В.Е. Гмурман. – 10-е изд., стер. – М.: Высш. шк., 2005. – 400с.
Вариант 1.
1. Запишите в виде дроби 
2. Для прядения смешаны поровну белый и окрашенный хлопок. Какова вероятность среди 5-ти случайно выбранных волокон смеси обнаружить менее 2-х окрашенных?
3. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, для второго - 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.
4. Среди 10 лотерейных билетов имеется 4 билета с выигрышем. Наудачу покупают 2 билета. Написать закон распределения вероятностей числа выигрышных билетов среди купленных.
5. Случайная величина Х имеет закон распределения:
| Х | |||
| Вер-ть | 0,7 | 0,1 | 0,2 |
Найти М(Х), D(X), s(X).
6. Случайная величина Х задана функцией распределения F(x). Найти а) плотность распределения вероятностей; б) вероятность попадания величины Х в заданный интервал (1; 2,5), если  .
.
7. В итоге измерений некоторой физической величины Х одним из приборов (без систематических погрешностей) получены результаты, приведенные в таблице. Найти: а) выборочную среднюю результатов измерений; б) выборочную и исправленную дисперсию ошибок приборов.
| 6,7 | 6,5 | 6,7 | 6,4 | 6,9 | 7,0 | 7,2 | 6,7 | 6,5 | 7,2 |
| 7,0 | 7,1 | 6,8 | 6,9 | 6,5 | 6,4 | 6,6 | 6,3 | 6,4 | 6,5 |
8. При анализе вещества двумя методами были получены указанные ниже результаты. В предположении нормальности распределения изучаемых величин проверить при уровне значимости р = 0,05 гипотезу о равенстве средних значений.  = 130;
= 130;  = 1;
= 1;  = 40;
= 40; 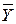 = 135;
= 135;  = 2;
= 2;  = 50.
= 50.
9. В таблице показано число деталей, изготовленных за смену рабочими одной бригады:
| № | Фамилия | Число деталей | № | Фамилия | Число деталей |
| Иванов | Семенов | ||||
| Лазарев | Лукин | ||||
| Ильин | Андреев | ||||
| Бережной | Попов | ||||
| Егоров | Сурков | ||||
| Петров |
Для представленного в таблице ряда чисел найдите среднее арифметическое, размах и моду. Какой смысл каждого из этих показателей?
Вариант 2.
1. Запишите в виде дроби 
2. Всхожесть семян данного сорта растений оценивается с вероятностью, равной 0,8. Какова вероятность того, что из 6-ти посеянных семян взойдет не менее 5-ти?
3. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,8. Найти вероятность того, что из 2-х проверенных изделий только одно стандартно.
4. В партии из 25 кожаных курток 5 имеют скрытый дефект. Покупают 3 куртки. Найти закон распределения числа дефектных курток среди купленных. Построить многоугольник распределения.
5. Случайная величина Х имеет закон распределения:
| Х | - 2 | -1 | ||
| Вер-ть | 0,1 | 0,2 | 0,5 | 0,2 |
Найти М(Х), D(X), s(X).
6. Случайная величина Х задана функцией распределения F(x). Найти а) плотность распределения вероятностей; б) вероятность попадания величины Х в заданный интервал (2; 3), если 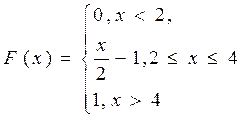 .
.
7. В итоге измерений некоторой физической величины Х одним из приборов (без систематических погрешностей) получены результаты, приведенные в таблице. Найти: а) выборочную среднюю результатов измерений; б) выборочную и исправленную дисперсию ошибок приборов.
| 8,9 | 8,6 | 9,0 | 8,5 | 8,4 | 9,3 | 8,9 | 8,3 | 8,9 | 8,6 |
| 8,7 | 8,9 | 8,6 | 9,0 | 8,5 | 8,2 | 8,4 | 8,6 | 8,9 | 8,7 |
8. При анализе вещества двумя методами были получены указанные ниже результаты. В предположении нормальности распределения изучаемых величин проверить при уровне значимости р = 0,05 гипотезу о равенстве средних значений.  = 3,5;
= 3,5;  = 0,01;
= 0,01;  = 15;
= 15; 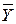 = 4;
= 4;  = 0,012;
= 0,012;  = 20.
= 20.
9. В ыборка задана в виде распределениячастот:
хi 4 7 8 12
mi 5 2 3 10
Найти распределение относительных частот.
Вариант 3.
1. Семь мальчиков, в число которых входят Олег и Игорь, становятся в ряд.
Найдите число возможных комбинаций, если:
а) Олег должен находиться в конце ряда;
б) Олег должен находиться в начале ряда, а Игорь – в конце ряда;
2. Два равносильных противника играют в шахматы. Что вероятнее выиграть: не менее 2-х партий из 4-х или не менее 3-х партий из 5-ти?
3. Вероятность того, что в течение одной смены возникает неполадка станка, равна 0,05. Какова вероятность того, что не произойдет ни одной неполадки за три смены?
4. Из партии в 20 изделий, среди которых имеется 6 бракованных, выбраны случайным образом 3 изделия для проверки их качества. Построить ряд распределения случайного числа Х - бракованных изделий среди отобранных.
5. Случайная величина Х имеет закон распределения:
| Х | ||||
| Вер-ть | 0,05 | 0,1 | 0,25 | 0,6 |
Найти М(Х), D(X), s(X).
6. Случайная величина Х задана функцией распределения F(x). Найти а) плотность распределения вероятностей; б) вероятность попадания величины Х в заданный интервал (1; 1,5), если  .
.
7. В итоге измерений некоторой физической величины Х одним из приборов (без систематических погрешностей) получены результаты, приведенные в таблице. Найти: а) выборочную среднюю результатов измерений; б) выборочную и исправленную дисперсию ошибок приборов.
| 7,9 | 7,6 | 8,0 | 7,6 | 7,4 | 7,6 | 7,8 | 8,0 | 7,7 | 8,0 |
| 7,8 | 7,7 | 7,9 | 7,5 | 7,6 | 7,8 | 8,1 | 7,6 | 7,7 | 7,6 |
8. При анализе вещества двумя методами были получены указанные ниже результаты. В предположении нормальности распределения изучаемых величин проверить при уровне значимости р = 0,05 гипотезу о равенстве средних значений.  = 60;
= 60;  = 3;
= 3;  = 50;
= 50; 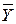 = 66;
= 66;  = 2,5;
= 2,5;  = 60.
= 60.
9. В ыборка задана в виде распределениячастот:
хi 2 5 7
mi 1 3 6
Найти распределение относительных частот.
Вариант 4.
1. Сколькими способами можно расставить на полке 12 книг, из которых 5 книг -
сборники стихов, так, чтобы сборники стихов стояли рядом в произвольном порядке?
2. Изделия некоторого производства содержат 5% брака. Найти вероятность того, что среди 5-ти взятых наугад изделий:1) нет ни одного испорченного; 2) будет 2 испорченных.
3. В ящике имеется 10 деталей, среди которых 6 окрашенных. Сборщик наудачу извлекает 4 детали. Найти вероятность того, что все извлеченные детали окажутся окрашенными.
4. В коробке 20 одинаковых катушек ниток, из них - 4 катушки с белыми нитками. Наудачу вынимают 2 катушки. Найти закон распределения числа катушек с белыми нитками среди вынутых.
5. Случайная величина Х имеет закон распределения:
| Х | 4,3 | 5,1 | 10,6 |
| Вер-ть | 0,2 | 0,3 | 0,5 |
Найти М(Х), D(X), s(X).
6. Случайная величина Х задана функцией распределения F(x). Найти а) плотность распределения вероятностей; б) вероятность попадания величины Х в заданный интервал ( ), если
), если 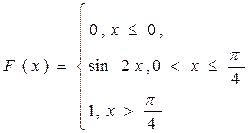 .
.
7. В итоге измерений некоторой физической величины Х одним из приборов (без систематических погрешностей) получены результаты, приведенные в таблице. Найти: а) выборочную среднюю результатов измерений; б) выборочную и исправленную дисперсию ошибок приборов.
| 4,3 | 4,5 | 4.7 | 4,9 | 4,5 | 4,6 | 4,8 | 4,3 | 4,7 | 4,2 |
| 4,8 | 4,9 | 5,0 | 4,7 | 4,6 | 4,4 | 4,3 | 4,6 | 4,8 | 4,7 |
8. При анализе вещества двумя методами были получены указанные ниже результаты. В предположении нормальности распределения изучаемых величин проверить при уровне значимости р = 0,05 гипотезу о равенстве средних значений.  = 172;
= 172;  = 2,5;
= 2,5;  = 40;
= 40; 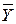 = 180;
= 180;  = 3;
= 3;  = 50.
= 50.
9. На соревнованиях по фигурному катанию судьи поставили спортсмену следующие оценки:
5,2; 5,4; 5,5; 5,4; 5,1; 5,1; 5,4; 5,5; 5,3. Для полученного ряда чисел найдите среднее арифметическое, размах и моду. Что характеризует каждый показатель?
Вариант 5.
1. Вычислите: 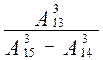 .
.
2. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель 2-х пуль и более, если выстрелов было 5000.
3. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором 3 вопроса.
4. Баскетболист делает три штрафных броска. Вероятность попадания при каждом броске равна 0,7. Построить ряд распределения числа попадания мяча в корзину.
5. Случайная величина Х принимает значения 7, - 2, 1, - 5, 3 с равными вероятностями. Найти М(Х).
6. Случайная величина Х задана функцией распределения F(x). Найти а) плотность распределения вероятностей; б) вероятность попадания величины Х в заданный интервал ( ), если
), если  .
.
7. В итоге измерений некоторой физической величины Х одним из
| 3,4 | 3,3 | 3,6 | 3,7 | 3,9 | 4,0 | 4,2 | 3,8 | 3,9 | 3,4 |
| 3,7 | 3,8 | 3,5 | 4,0 | 4,1 | 4,2 | 3,7 | 3,3 | 3,5 | 3,6 |
приборов (без систематических погрешностей) получены результаты, приведенные в таблице:
Найти: а) выборочную среднюю результатов измерений; б) выборочную и исправленную дисперсию ошибок приборов.
8. При анализе вещества двумя методами были получены указанные ниже результаты. В предположении нормальности распределения изучаемых величин проверить при уровне значимости р = 0,05 гипотезу о равенстве средних значений.  = 95,2;
= 95,2;  = 0,04;
= 0,04;  = 8;
= 8; 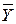 = 96,8;
= 96,8;  = 0,06
= 0,06  = 9.
= 9.
9. Построить полигон частот по данному распределению выборки:
хi 2 3 5 6
mi 10 15 5 20
Вариант 6.
1. Вычислите: 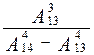 .
.
2. Что вероятнее выиграть у равносильного противника (ничья не принимается): 3 партии из 4-х или 5 из 8-и?
3. В первой урне содержится 10 шаров, из них 8 белых; во второй урне содержится 20 шаров, из них 4 белых. Из каждой урны наугад извлекают по одному шару, а затем из этих двух шаров наугад взят один шар. Найти вероятность того, что взят белый шар.
4. Имеются три базы с независимым снабжением. Вероятность отсутствия на базе нужного товара равна 0,1. Предприниматель решил закупить некий товар. Составить закон распределения числа баз, на которых в данный момент этот товар отсутствует.
5. Случайные величины Х и У имеет законы распределения:
| У | - 1 | |||
| Вер-ть | 0,1 | 0,3 | 0,5 | 0,1 |
| Х | - 1 | ||
| Вер-ть | 0,2 | 0,3 | 0,5 |
Найти: М (3Х – 1) и D(X).
6. Случайная величина Х задана функцией распределения F(x). Найти а) плотность распределения вероятностей; б) вероятность попадания величины Х в заданный интервал (3; 4), если  .
.
7. В итоге измерений некоторой физической величины Х одним из приборов (без систематических погрешностей) получены результаты, приведенные в таблице:
| 2,3 | 2,7 | 2,5 | 2,3 | 2,4 | 2,5 | 2,8 | 2,7 | 2,3 | 2,4 |
| 2,6 | 2,9 | 2,7 | 2,5 | 2,8 | 3,0 | 3,1 | 2,8 | 2,9 | 2,7 |
Найти: а) выборочную среднюю результатов измерений; б) выборочную и исправленную дисперсию ошибок приборов.
8. При анализе вещества двумя методами были получены указанные ниже результаты. В предположении нормальности распределения изучаемых величин проверить при уровне значимости р = 0,05 гипотезу о равенстве средних значений.  = 90;
= 90;  = 4,5;
= 4,5;  = 55;
= 55; 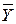 = 93;
= 93;  = 3;
= 3;  = 60.
= 60.
9. В таблице показано распределение призывников по росту:
| Рост, см | 155-160 | 160-165 | 165-170 | 170-175 | 175-180 | 180-185 | 185-190 | 190-195 |
| частота |
Постройте гистограмму, характеризующую распределение призывников по росту.
Вариант 7.
1. Вычислите: 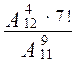 .
.
2. Найти вероятность того, что событие А появится не менее 3-х раз в 4-х независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4.
3. Устройство содержит 2 независимо работающих элемента. Вероятность отказа элементов равна соответственно 0,05 и 0,08. Найти вероятность отказа устройства, если для этого достаточно, чтобы отказал хотя бы один из элементов.
4. Бросают три игральных кубика. Составить закон распределения числа выпавших «шестерок» на трех кубиках. Построить многоугольник распределения.
5. Случайные величины Х и У имеет законы распределения:
| У | - 1 | |||
| Вер-ть | 0,1 | 0,3 | 0,5 | 0,1 |
| Х | - 1 | ||
| Вер-ть | 0,2 | 0,3 | 0,5 |
Найти: М (2Х – 3У) и D (2X).
6. Случайная величина Х задана функцией распределения F(x). Найти а) плотность распределения вероятностей; б) вероятность попадания величины Х в заданный интервал (3,5; 4), если  .
.
7. В итоге измерений некоторой физической величины Х одним из приборов (без систематических погрешностей) получены результаты, приведенные в таблице:
| 1,8 | 1,9 | 1,5 | 1,6 | 1,8 | 1,7 | 1,4 | 1,6 | 1,5 | 1,7 |
| 1,9 | 2,0 | 2,1 | 1,8 | 1,6 | 1,7 | 1,5 | 1,7 | 1,8 | 1,9 |
Найти: а) выборочную среднюю результатов измерений; б) выборочную и исправленную дисперсию ошибок приборов.
8. При анализе вещества двумя методами были получены указанные ниже результаты. В предположении нормальности распределения изучаемых величин проверить при уровне значимости р = 0,05 гипотезу о равенстве средних значений.  = 60,8;
= 60,8;  = 0,03;
= 0,03;  = 7;
= 7; 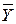 = 62,3;
= 62,3;  = 0,02;
= 0,02;  = 9.
= 9.
9. Наблюдая за работой бригады токарей, установили, сколько времени тратили они на обработку одной детали. По данным составили таблицу:
| Время, мин | 10-12 | 12-14 | 14-16 | 16-18 | 18-20 |
| Число токарей |
Постройте гистограмму, характеризующую распределение токарей бригады по времени, затраченному на обработку одной детали.
Вариант 8.
1. Вычислите: 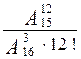 .
.
2. Событие В появится в случае, если событие А наступит не менее 4-х раз. Найти вероятность наступления события В, если будет произведено 5 независимых испытаний, в каждом их которых вероятность появления события А равна 0,8.
3. Имеется два одинаковых ящика с шарами. В первом ящике находится 2 белых и 1 черный шар, во втором – 3 белых и 4 черных шара. Наугад выбирают один ящик и вынимают из него шар. Какова вероятность того, что вынутый шар окажется белым.
4. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента 0,15. Составить закон распределения отказавших элементов.
5. Случайные величины Х и У имеет законы распределения:
| У | - 1 | |||
| Вер-ть | 0,1 | 0,3 | 0,5 | 0,1 |
Найти: М (У 2 ) и D(У).
6. Случайная величина Х задана функцией распределения F(x). Найти а) плотность распределения вероятностей; б) вероятность попадания величины Х в заданный интервал (0; 1), если 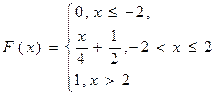 .
.
7. В итоге измерений некоторой физической величины Х одним из приборов (без систематических погрешностей) получены результаты, приведенные в таблице:
| 9,4 | 9,6 | 9,7 | 9,4 | 9,3 | 9,6 | 9,8 | 9,9 | 10,1 | |
| 9,8 | 9,7 | 10,2 | 9,6 | 9,7 | 9,8 | 9,7 | 9,8 | 9,9 |
Найти: а) выборочную среднюю результатов измерений; б) выборочную и исправленную дисперсию ошибок приборов.
8. При анализе вещества двумя методами были получены указанные ниже результаты. В предположении нормальности распределения изучаемых величин проверить при уровне значимости р = 0,05 гипотезу о равенстве средних значений.  = 85,5;
= 85,5;  = 2,5;
= 2,5;  = 40;
= 40; 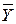 = 90,5;
= 90,5;  = 1,5;
= 1,5;  = 50.
= 50.
9. В таблице показано число изделий, изготовленных за месяц членами артели:
| № | Фамилия | Число деталей | № | Фамилия | Число деталей |
| Антонов | Квитко | ||||
| Астафьев | Лазарев | ||||
| Баранов | Осокин | ||||
| Бобков | Рысаев | ||||
| Васильев | Сухов | ||||
| Егоров | Чернышов |
Найдите медиану этого ряда данных. У кого из членов артели выработка за месяц была больше медианы?
Вариант 9.
1. Найдите натуральное число х, для которого выполняется равенство: 
2. Монету бросают 5 раз. Найти вероятность того, что герб выпадет: 1) менее 2-х раз; 2) не менее 2-х раз.
3. В ящике 10 красных и 8 синих пуговиц. Вынимают наугад 2 пуговицы. Какова вероятность того, что пуговицы будут одноцветными.
4. Вероятность того, что при составлении бухгалтерского баланса допущена ошибка, равна 0,3. Аудитору на заключение представлено 3 баланса предприятия. Составить закон распределения числа положительных заключений на проверяемые балансы.
5. Даны законы распределения двух независимых случайных величин:
Х 2 4 6 8 У 0 1 2
Вер-ть 0,4 0,2 0,1 0,3 Вер-ть 0,5 0,2 0,3.
Найти математическое ожидание величины Z = 2X + 3У.
6. Случайная величина Х задана функцией распределения F(x). Найти а) плотность распределения вероятностей; б) вероятность попадания величины Х в заданный интервал ( ), если
), если 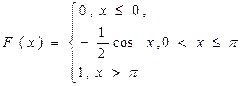 .
.
7. В итоге измерений некоторой физической величины Х одним из приборов (без систематических погрешностей) получены результаты, приведенные в таблице:
| 11,4 | 11,2 | 11,3 | 11,6 | 11,4 | 11,3 | 11,7 | 11,6 | 11,8 | 11,7 |
| 11,8 | 11,9 | 11,6 | 11,7 | 11,5 | 11,4 | 11,2 | 11,3 | 11,1 | 11,1 |
Найти: а) выборочную среднюю результатов измерений; б) выборочную и исправленную дисперсию ошибок приборов.
8. При анализе вещества двумя методами были получены указанные ниже результаты. В предположении нормальности распределения изучаемых величин проверить при уровне значимости р = 0,05 гипотезу о равенстве средних значений.  = 70,5;
= 70,5;  = 0,04;
= 0,04;  = 15;
= 15; 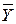 = 71,4;
= 71,4;  = 0,05;
= 0,05;  = 20.
= 20.
9. В супермаркете проводились наблюдения над числом покупателей, обратившихся в кассу за один час. Наблюдения в течение 30 часов дали следующие результаты: 70, 75, 100, 120, 75, 60, 100, 120, 70, 60, 65, 100, 65, 100, 70, 75, 60, 100, 120, 100, 70, 75, 70, 120, 65, 70, 75, 70, 100, 100. Полученные данные представляют собой выборку объема 30. Требуется составить ряд распределения частот (вариационный ряд).
Вариант 10.
1. Найдите натуральное число х, для которого выполняется равенство: 
2. Вероятность того, что любой абонент позвонит на коммутатор в течение часа, равна 0,01. Телефонная станция обслуживает 800 абонентов. Какова вероятность того, что в течение часа позвонят 5 абонентов.
3. В читальном зале имеется 6 учебников по теории вероятностей, из которых 3 в переплете. Библиотекарь наугад взял 2 учебника. Найти вероятность того, что оба учебника окажутся в переплете.
4. Вероятность того, что аудитор допустит ошибку при проверке бухгалтерского баланса равна 0,05. Аудитору на заключение представлено 2 баланса. Составить закон распределения числа правильных заключений на проверяемые балансы.
5. Даны законы распределения двух независимых случайных величин:
Х 2 4 6 8 У 0 1 2
Вер-ть 0,4 0,2 0,1 0,3 Вер-ть 0,5 0,2 0,3.
Найти дисперсию величины Z = 2X + 3У.
6. Случайная величина Х задана функцией распределения F(x). Найти а) плотность распределения вероятностей; б) вероятность попадания величины Х в заданный интервал ( ), если
), если  .
.
7. В итоге измерений некоторой физической величины Х одним из приборов (без систематических погрешностей) получены результаты, приведенные в таблице:
| 15,2 | 15,1 | 15,3 | 15,4 | 15,7 | 15,6 | 15,5 | 15,4 | 15,6 | 15,7 |
| 15,6 | 15,8 | 15,5 | 15,7 | 15,9 | 16,0 | 15,8 | 15,6 | 15,5 | 15,9 |
Найти: а) выборочную среднюю результатов измерений; б) выборочную и исправленную дисперсию ошибок приборов.
8. При анализе вещества двумя методами были получены указанные ниже результаты. В предположении нормальности распределения изучаемых величин проверить при уровне значимости р = 0,05 гипотезу о равенстве средних значений.  = 5,4;
= 5,4;  = 0,04;
= 0,04;  = 10;
= 10; 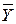 = 6;
= 6;  = 0,043;
= 0,043;  = 15.
= 15.
9. Наблюдается число выигрышей в мгновенной лотерее. В результате наблюдений получены следующие значения выигрышей (тыс. руб.): 0, 1, 0, 0, 5, 0, 10, 0, 1, 0, 0, 1, 5, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 5, 0, 5, 0, 0, 1, 1, 1, 5, 10, 0, 1, 1, 0, 5, 0, 0, 0, 0, 1, 0, 1, 0, 5, 0, 0, 0, 0, 1, 0. Составить вариационный ряд выигрыша в мгновенной лотерее.
Поиск по сайту: