АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Коды хэмминга

Читайте также:
  1. Самокорректирующие коды (коды Хемминга). Примеры построения кодов Хэмминга.

Это линейные блочные коды с параметрами , где 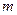- положительное целое число, - число проверочных символов. Для задания кодов Хэмминга обычно используется проверочная матрица. Ее столбцами являются все ненулевые двоичные числа длиной .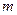

Они обладают кодовым расстоянием и способны исправлять только одну или обнаруживать две ошибки.

Примеры полных кодов Хэмминга: (7, 4), (15, 11), (31, 26), (63, 57).

Пример 3.5:

Рассмотрим код Хэмминга (7, 4). Проверочная матрица:

Порождающая матрица:

.

Модификациями кодов Хэмминга являются укороченные и удлиненные коды Хэмминга.

Чтобы получить проверочную матрицу укороченного кода Хэмминга, необходимо в проверочной матрице полного кода исключить любые Т столбцов, относящиеся к информационным разрядам, где Т - параметр укорочения.

Удлиненные коды Хэмминга получаются путем введения дополнительной проверки на четность всех символов кодового слова.

Коды Хэмминга обладают очень слабой корректирующей способностью и отдельно практически не используются. Очень хорошие результаты позволяет получить применение данных кодов в составе каскадных схем кодирования. Каскадные коды состоят из двух или более кодов: кодовые слова одного кода являются информационными символами для кода следующей ступени.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)