Мажоритарное декодирование

Основано на том, что каждый информационный символ можно выразить через другие символы кодового слова с помощью линейных соотношений. Окончательное решение о значении символа принимается по мажоритарному принципу (по большинству) результатов таких проверок.

Существует три способа построения систем проверочных уравнений для декодирования символа:

- системы с разделенными проверками – символ, относительно которого разделяется система, входит во все уравнения. Любой другой символ входит не более, чем в одно уравнение. Для коррекции ошибок необходимо 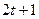уравнений в системе;

- системы с 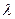-связанными проверками – символ, относительно которого разрешается система, входит во все уравнения. Любой другой символ входит не более, чем в 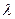уравнений. Для коррекции ошибок необходимо уравнений в системе;

- системы с квазиразделенными проверками – система разделима относительно некоторой суммы символов. На первом этапе она разрешается относительно суммы символов, а на втором – относительно конкретного символа.

Рисунок 5.2 – Структурная схема мажоритарного декодера.

На рисунке: 1…k – устройства, реализующие проверки для соответствующей системы; МЭ – мажоритарный элемент, принимающий решение о значении символа по большинству результатов проверок.

Пример 5.1:

Код (8,4) задан матрицей:

.

Система уравнений по матрице Н:

Система проверочных уравнений для :

Система проверочных уравнений для :

Система проверочных уравнений для :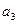

Система проверочных уравнений для :

Пусть .

Результат декодирования: .

Поиск по сайту: