Ощие сведения

Сущность оптимального приема состоит в том, чтобы для выделения переданного сигнала использовать такие преобразования принимаемого колебания на выходе канала передачи, при которых обеспечивается наибольшая помехоустойчивость. Совокупность таких преобразований называют алгоритмом оптимального приема данного сигнала при передаче его по данному каналу.

В цифровых системах связи, как правило, применяется поэлементный прием. Поэлементный (посимвольный) прием – способ приема, при котором решение о переданном сигнале принимается отдельно для каждого сигнала, независимо от принятого ранее.

В теории приема сигналов пользуются различными критериями оптимальности. Критерий оптимальности приема – признак, на основании которого производится оценка обработки принятого сигнала как наилучшая. Его выбор зависит от условий работы.

При передаче дискретных сигналов широко используется критерий идеального наблюдателя (критерий котельникова). Согласно ему тот приемник считается оптимальным, который обеспечивает минимум полной вероятности ошибки. Записывается в виде:

.

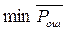Полная вероятность ошибки 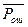вычисляется как математическое ожидание вероятности ошибки каждого из первичных сигналов :

,

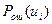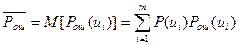где 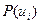- вероятность передачи сигнала ;

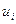- общее число первичных сигналов.

На практике наиболее часто встречается случай передачи двоичных первичных сигналов сигналами, сформированными методами АМн, ЧМн и ФМн, в канале с аддитивным гауссовским шумом.

Аддитивная помеха – помеха, мгновенные значения которой складываются с мгновенными значениями сигнала. Гауссовский шум представляет собой стационарный эргодический случайный процесс с гауссовским (нормальным) распределением вероятности.

Таблица 27.1 – Алгоритмы оптимального приема при аддитивном гауссовском шуме.

Вид модуляции	Алгоритм
АМн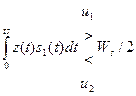
ЧМн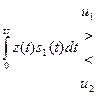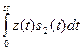
ФМн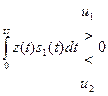

Использованные в таблице обозначения:

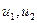- двоичные первичные сигналы, соответствующие символам «1» и «0»;

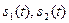- модулированные сигналы длительности 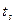с различными амплитудами (при АМн), частотами (при ЧМн) или фазами (при ФМн);

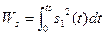- энергия сигнала ;

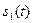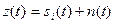- принятая сумма сигнала и помехи.

Приведенные алгоритмы можно реализовать двумя способами: на основе корреляторов, на основе согласованных фильтров.

Коррелятор (активный фильтр) – устройство, состоящее из трех блоков: перемножителя, генератора и интегратора - и используемое для вычисления скалярного произведения сигналов 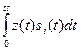. Используется в случае, когда сигналы имеют сложную форму.

Поэтому приведенные на рисунке 27.1 схемы получили название оптимальных корреляционных приемников.

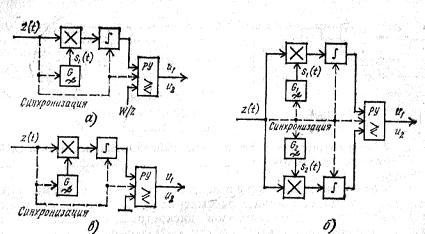
Рисунок 27.1 – Структурные схемы оптимальных когерентных приемников на корреляторах: а – АМн сигналов; б – ЧМн сигналов; в – ФМн сигналов.

Используемые обозначения:

- генераторы опорных сигналов 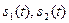, форма которых повторяет форму обнаруживаемых сигналов;

- перемножитель;

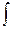- интегратор;

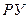- решающее устройство.

Схемы приемников сигналов с АМн и ФМн одноканальные (имеют одну ветвь обработки), с ЧМн – двухканальные (имеют две ветви обработки). В РУ результат интегрирования сравнивается с порогом, равным половине энергии сигнала 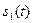для АМн, и нулевым для ФМн либо результаты интегрирования сравниваются друг с другом для ЧМн. На выходе РУ формируются первичные сигналы в зависимости от знака неравенства.

Для работы генераторов, интеграторов и решающего устройства используются синхронизирующие тактовые импульсы, получаемые от специального устройства. Эти импульсы определяют начало и конец интервала интегрирования и момент вынесения решения о принятом сигнале.

Согласованный фильтр (СФ) – пассивный линейный фильтр с постоянными параметрами и импульсной характеристикой:

,

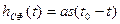где 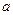- произвольный коэффициент пропорциональности;

- сигнал длительностью 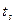, по отношению к которому данный фильтр является согласованным;

- задержка в фильтре или момент отсчета.

Импульсная характеристика – реакция линейного четырехполюсника на воздействие в виде очень короткого прямоугольного импульса с достаточно большой амплитудой.

Импульсная характеристика согласованного с сигналом фильтра совпадает с зеркальным изображением этого сигнала, сдвинутым в положительном направлении по оси времени на длительность .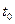

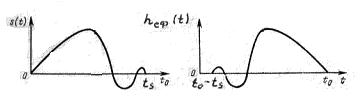
Рисунок 27.2 – Сигнал и импульсная характеристика согласованного с ним фильтра при .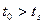

Форма сигнала на выходе СФ существенно отличается от формы сигнала на входе. Отношение сигнал-помеха на выходе СФ является максимально достижимым для линейных фильтров. СФ обеспечивает максимально возможное мгновенное значение сигнала на выходе в момент отсчета на сигнал, с которым он согласован. Оно численно равно энергии этого сигнала.

Рисунок 27.2 – Форма сигналов на входе и выходе СФ.

СФ в схемах приемников заменяют генераторы, перемножители и интеграторы.

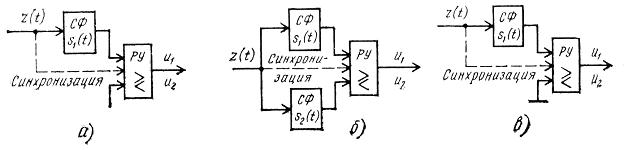
Рисунок 27.3 – Структурные схемы оптимальных когерентных приемников на СФ: а – АМн сигналов; б - ЧМн сигналов; в – ФМн сигналов.

Поиск по сайту: