 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Декодирование по синдрому
|
Читайте также: |
Основано на стандартной таблице – таблице всех возможных принятых из канала слов, организованной таким образом, что может быть найдено ближайшее к принятому кодовое слово. Она содержит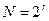 
строк и 
столбцов.
Таблица – Стандартная таблица.
| s1 =(0…0) r | b1 =(0…0) n | b2 | … | bM |
| s2 … sN | e2 … eN | b2+e2 … b2+eN | … … … | bM+e2 … bM+eN |
b i – кодовые слова;
e j – векторы ошибок – образцы ошибок минимального веса;
b i+ e j – слова, не являющиеся кодовыми;
s i= e i∙HT – синдромы – векторы размерностью r, указывающие на наличие и расположение ошибок в принятом слове.
Правило декодирования:
1. Вычисляется синдром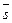 
по принятому слову 
:
.
Если 
, то является кодовым словом. В противном случае (
) содержит ошибки.
2. По 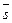находится наиболее правдоподобный вектор ошибки 
.
3. Ближайшее к принятому кодовое слово 
получается в результате суммирования и :
.
Рисунок 5.3 – Структурная схема декодера по синдрому.
На рисунке: Б – буфер хранения принятого слова; БВС – блок вычисления синдрома; С – селектор (дешифратор) синдрома; К – корректор.
Данный метод используется, когда число проверочных символов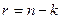 
мало (<10).
Пример:
Составить стандартную таблицу для систематического кода (5,2) с порождающей матрицей:
.
Таблица должна содержать 
строк и 
столбцов.
Таблица – Стандартная таблица.
| b1 =(00000) | b2 =(01011) | b3 =(10101) | b4 =(11110) | s1 =(000) |
| e2 =(00001) | b2+e2 =(01010) | b3+e2 =(10100) | b4+e2 =(11111) | s2=e2∙HT =(001) |
| e3 =(00010) | b2+e3 =(01001) | b3+e3 =(10111) | b4+e2 =(11100) | s3=e3 ∙ HT =(010) |
| e4 =(00100) | b2+e4 =(01111) | b3+e4 =(10001) | b4+e2 =(11010) | s4=e4∙HT =(100) |
| e5 =(01000) | b2+e5 =(00011) | b3+e5 =(11101) | b4+e2 =(10110) | s5=e5∙HT =(011) |
| e6 =(10000) | b2+e6 =(11011) | b3+e6 =(00101) | b4+e2 =(01110) | s6=e6∙HT =(101) |
| e7 =(01100) | b2+e7 =(00111) | b3+e7 =(11001) | b4+e2 =(10010) | s7=e7∙HT =(111) |
| e8 =(11000) | b2+e8 =(10011) | b3+e8 =(01101) | b4+e2 =(00110) | s8=e8∙HT =(110) |
Пусть 
(10111). Проведем декодирование.
1. 
;
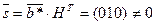2. 
;
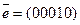3. 
.
ДОМАШНЕЕ ЗАДАНИЕ:
1. [3.1.2] с. 309…312, 317…318;
[3.1.3] с. 205…208;
[3.1.5] с. 147.. 149, 150…151;
[3.1.14] с. 258…261, 271…273.
2. Код (7,4) задан порождающей матрицей:
.
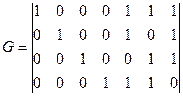Провести декодирование по синдрому принятого слова 
.
6 НЕПРЕРЫВНЫЕ (РЕКУРРЕНТНЫЕ) КОДЫ
Поиск по сайту: