АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Матричный метод разбиения

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Методические основы
  3. I. Предмет и метод теоретической экономики
  4. II. Метод упреждающего вписывания
  5. II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
  6. II. Методы непрямого остеосинтеза.
  7. II. Проблема источника и метода познания.
  8. II. УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА ДИСЦИПЛИНЫ
  9. III. Методологические основы истории
  10. III. Предмет, метод и функции философии.
  11. III. Социологический метод
  12. III. УЧЕБНО – МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ ПО КУРСУ «ИСТОРИЯ ЗАРУБЕЖНОЙ ЛИТЕРАТУРЫ К. XIX – НАЧ. XX В.»

Метод разбиения графа на максимальные сильно связные подграфы по матрицам достижимости R и контрдостижимости Q состоит в следующем:

 

1. По матрице смежности строится матрица достижимости R.

Используя операцию транспонирования, находим матрицу контрдостижимости Q.

 

2. Находится матрица С ={Сij}, ij = 1,2,3,...n, где n

- число вершин исходного графа, а каждый элемент

Сij = Rij*Qij, т. е. матрица С получается поэлементным логическим умножением матриц R и Q.

 

3. Элементы, имeющиe одинаковые строки и столбцы в матрице

С группируются перестановкой строк, получаем (строчeчно диагональную матрицу Св, где каждая группа элементов и есть максимальный сильно связный подграф.

 

Для нахождения матрицы достижимости определены транзитивные замыкания, представленные на рис.7. Сама матрица достижимости показана на рис.8.

 

 

Т+(Хi)

 
 

 
 


Рис. 7

 
 

Рис. 8

 

Используя операцию транспонирования, находится матрица Q, изображённая на рис.9.

 
 

Рис. 9

Перемножая логически матрицы R*Q, получена матрица С, изображённая на рис.10.

 
 

Рис.10

 

 
 

Элементы, имeющиe одинаковые строки и столбцы в матрице группируются перестановкой строк, получена строчeчно диагональная матрица Св, изображённая на рис.11.

Рис.11

 

Каждая группа элементов и есть максимальный сильно связный подграф. Итак, получены максимальные сильно связный подграфы:

G1=(X1,A1), Х1={2,4,5,6,7,10,11,14,15,16,17,19,21,22,23,24,25}

G2=(X2,A2), Х2={1,8,12,20}

G3=(X3,A3), Х3={3,8,13,18}


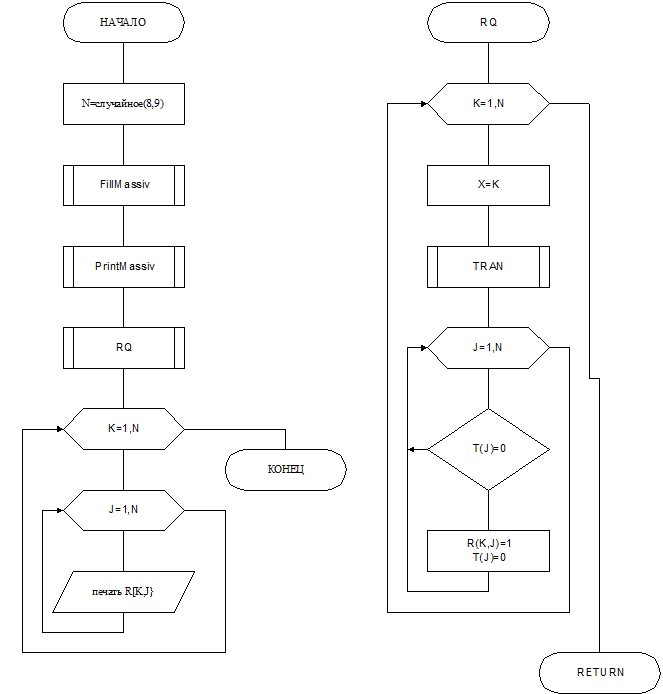
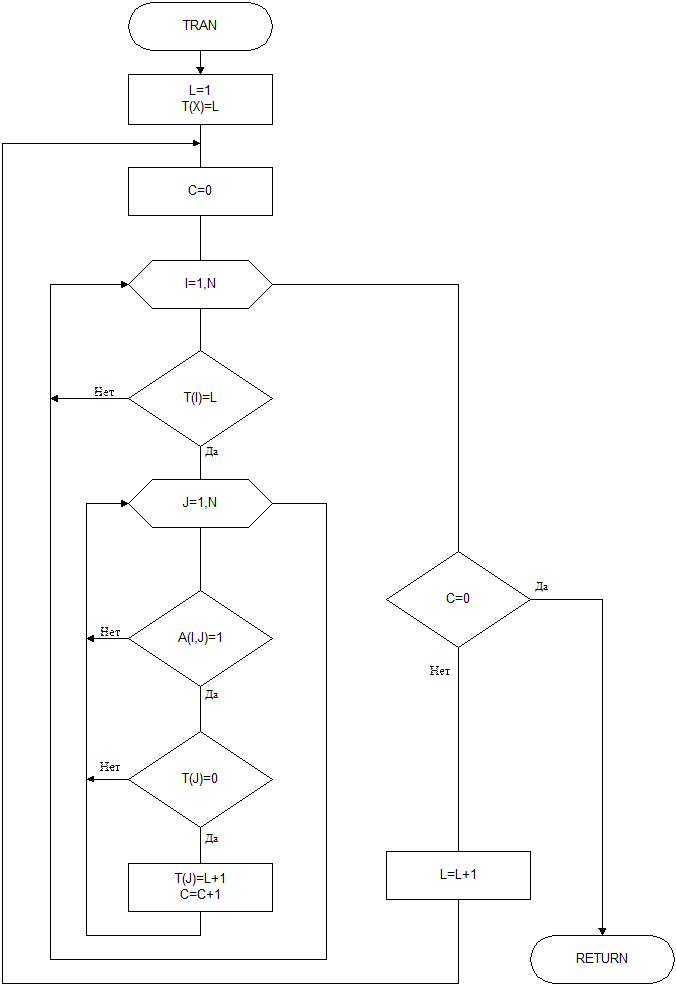
Приложение 4


Приложение 4

 


 

 

Волченская Тамара Викторовна

 


1 | 2 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)