Определение риска портфеля ценных бумаг

Сегодняшняя статья «Риск портфеля ценных бумаг» описывает, что такое риск портфеля, его измерение, формулы расчета. Итак, при анализе риска обычно используются различные статистичекие методы, однако при анализе риска портфеля ценных бумаг представляют собой сочетание разных стандартных отклонений активов, которые в него входят. По причине того, что разные активы по-разному ведут себя во время конъюнктурных изменений рынка, риск портфеля почти всегда не равен средневзвешенной величине стандартных отклонений активов, которые в него входят. Для того, чтобы измерить степень взаимосвязи и различные направления изменения разных доходностей 2-ух активов обычно используются показатели ковариации и корреляции (статистические показатели).

Формула расчета ковариации приведена на рисунке 1, где i1, i2 – это доходность первого или второго актива в k-ом периоде, а данные показатели с чертой – это средняя доходность данных активов за n периодов. Если после расчета ковариация со знаком плюс, то доходности по активам изменяют в одном направлении, а минус свидетельствует о противоположных направлениях. Если они достигают практически нуля, то зависимость слабо выражена.

Ковариация зависит также от единицы измерения, поэтому ее использование на практике является очень сложным процессом.Коэффициент корреляции является производным ковариации и рассчитывается по формуле, изображенной на рисунке 2. Данный коэффициент обладает свойствами ковариации, но является в тоже время безразмерной величиной, принимая при этом значения от +1 до -1; если величины независимы, то его значение практически равно нулю.

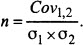
Стандартное отклонение портфеля ценных бумаг при двух активах рассчитывается по формуле 3 (рисунок 3), где W1 и W2 – удельный вес соответствующих активов в портфеле, а сигма один и два – это стандартные отклонения в доходности соответствующих активов; р1-2 – корреляция между первым и вторым активами.

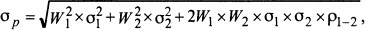
Если производить расчет риска портфеля ценных бумаг, который состоит из нескольких активов, то надо учитывать парные корреляции или ковариации всех активов, которые в него входят. Формула 4 (рисунок 4) показывает как это рассчитать. Причем Wk, Wm – удельный вес k-го (m-го) актива в портфеле.

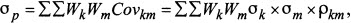
Если объединять портфели ценных бумаг с корреляцией +1, то риск портфеля не уменьшается, а только усредняется. Идеальным портфелем можно считать только такой портфель, где корреляция равна -1. Риск портфеля ценных бумаг становиться меньше средневзвешенной суммы рисков, когда между активами корреляция отрицательная. Поэтому, если инвестор формирует актив с низкой корреляцией доходностей, то данный случай называют хеджированием. Для оценки риска портфеля ценных бумаг необходимо в первую очередь рассчитать среднюю фактическую доходность данного портфеля за n-периодов, следующим этапом является расчет риска портфеля по показателю среднеквадратического отклонения, а уже последним этапом (третьим) является сравнение совокупный коэффициент вариации с другими портфелями ценных бумаг, который рассчитывается по формуле 5 (рисунок 5), где iр – средняя фактическая доходность портфеля ценных бумаг за n периодов, а сигма р – среднеквадратическое отклонение портфеля ценных бумаг.

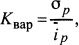
Поиск по сайту: