 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Индивидуальные задания. Решение нелинейных уравнений
Решение нелинейных уравнений
Цель: изучить основные возможности приложения Microsoft Excel для решения нелинейных уравнений.
Задание
Найти все действительные корни нелинейного уравнения  с относительной погрешностью
с относительной погрешностью  .
.
Методические указания
1. Построить график функции  как показано на рис.6.1.
как показано на рис.6.1.
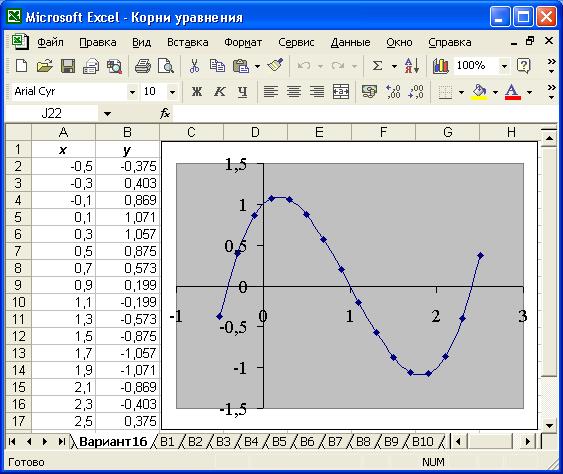
Рис.6.1. Результаты табулирования и построения графика функции 
2. Пользуясь графиком, определить точки, в которых значения функции равны нулю:  – это и есть приближенные значения корней уравнения.
– это и есть приближенные значения корней уравнения.
3. Уточнить значения корней с заданной относительной погрешностью  . Для этого открыть новый лист и назвать его, например, Корни уравнения. Будем искать вычисленные значения корней в ячейке A1, а уравнение занесем в ячейку B1.
. Для этого открыть новый лист и назвать его, например, Корни уравнения. Будем искать вычисленные значения корней в ячейке A1, а уравнение занесем в ячейку B1.
4. Занести в ячейку A1 приближенное значение первого корня: -0,5.
5. В ячейку B1 занести левую часть уравнения, используя в качестве независимой переменной x адрес ячейки A1.
6. В меню Сервис\Параметры…\Вычисления в поле Относительная погрешность: установить значение 0,00001.
7. Дать команду Сервис\Подбор параметра….
8. В открывшемся диалоговом окне Подбор параметра в поле Установить в ячейке: указать адрес ячейки, в которую занесена левая часть уравнения (B1), в поле Значение: задать значение правой части уравнения (0), а в поле Изменяя значение ячейки: указать адрес ячейки, в которую занесен аргумент (A1).
9. Щелкнуть на кнопке OK и проанализировать результат, отображаемый в диалоговом окне Результат подбора параметра. Щелкнуть на кнопке OK, чтобы сохранить полученные значения ячеек, участвовавших в операции.
10. Повторить расчет, задавая в ячейке A1 приближенные значения корней 1,0 и 2,5. Полученные результаты занести в таблицу, как показано на рис. 6.2.
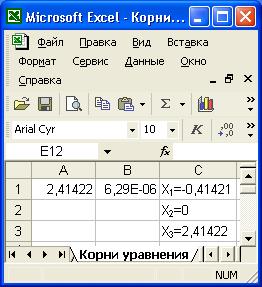
Рис.6.2. Результаты вычисления корней нелинейного уравнения
Индивидуальные задания
Найти все действительные корни нелинейных уравнений с относительной погрешностью  .
.
| Номер вар-та | Уравнение f(x)=0 | Номер вар-та | Уравнение f(x)=0 |

| 
| ||

| 
| ||

| x·2x=1 | ||

| 
| ||
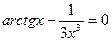
|  = = 
| ||

| 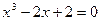
| ||

| 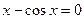
| ||
| 5x-3x = 2 | 
| ||
| 2ex - 5x=0 | 
| ||
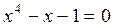
| 
| ||

| 
| ||

| 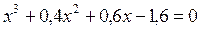
| ||

| 
| ||

| 
| ||

| 
| ||
| 3x-1+2+x = 0 | 
| ||
2arctg x -  = 0 = 0
| (2-x) - ex = 1 | ||

| x3+3x2+12x +3 = 0 | ||
| x4-18x2+6 = 0 | 2,2x+2x= 0 | ||
| (x-4)2·log 0,5(x-3) = -1 | x3-0,2x2+0,5x-1= 0 | ||
| x2·2x= 1 | x2+4sinx = 10 | ||
| 5-sinx = x | x3-0,1x2+0,4x + 1,2= 0 | ||
| e-2x-2x+1 = 0 | 2x-lgx =2 | ||
| 5x-6x -3 = 0 | x3-3x2+6x-5 = 0 | ||
| x4+4x3-8x2-17 = 0 | 5x-8lnx = 8 | ||
| x4-x3-2x2+3x-3 = 0 | x3-0,2x2+0,5x-1,4 = 0 | ||
| 0,5x-1 = (x+2)2 | 3x + ex= 2 | ||
| 2x2-0,5x-3 = 0 | x3+2x+4 = 0 | ||
| x2-cos2x = 1 | x(x+1)2= 1 | ||

| x3-3x2+12x-12 =0 | ||

| x = (x+1)3 | ||

| x3+0,2x2+0,5x+0,8 = 0 | ||
| 3x4+4x3-12x2+1 = 0 | 
| ||
| 3x4-8x3-18x2+2 = 0 | x3+4x-6 = 0 | ||
| (x-2)2×2x= 1 | 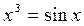
| ||
2sin 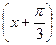 =0,5x2-1 =0,5x2-1 
| x3+0,1x2+0,4x-1,2 = 0 | ||
| x2-20sinx = 0 | x = 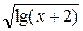 -5 -5
| ||

| x3+3x2+6x-1= 0 | ||
| 3x+2x-2 = 0 | 
| ||
| 2arctgx-3x+2 = 0 | x3-0,1x2+0,4x-1,5 = 0 | ||
| 2x4-8x3+8x2-1= 0 | 2x+lgx = -0,5 | ||
| 2x4+8x3+8x2-1= 0 | x3-3x2+6x-2= 0 | ||
| [(x-2)2-1]×2x= 1 | 2x-cosx = 0,5 | ||
| [log2(x+2)](x-1)= 1 | x3-0,2x2+0,3x-1,2= 0 | ||
| sin(x-0,5)-x+0,5= 0 | sin(0.5+x)= 2x-0,5 | ||
| 3x+2x-5= 0 | x3-3x2+12x-9= 0 | ||
| 2 ex + 3 x+1= 0 | 0,5x+lg(x-1)= 0,5 | ||
| x4-4x3-8x2+1= 0 | x3+0,2x2+0,5x-2 = 0 | ||
| 3x4+4x3-12x2-5= 0 | x3+3x+1 = 0 | ||

| 
|
Поиск по сайту: