 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задания для практической работы
ПРАКТИЧЕСКАЯ РАБОТА
Тема: Расчёт вала при кручении.
Цель: Для заданного вала построить эпюры крутящих моментов. Определить углы закручивания на каждом участке вала.
Пример
Дано: На распределительном валу установлены четыре шкива (рисунок 1), на вал через шкив 1 подаётся мощность Р1, которая через шкивы 2, 3, 4 передаётся потребителю. Вал вращается с постоянной угловой скоростью.
Р1 = 30 кВт; Р2 = 10 кВт; Р3 = 12 кВт; Р4 = 8 кВт; l1 = 0,4 м; l2 = 0,3 м; l3 = 0,5 м; ω = 100 рад/с.
Рисунок 1 – Распределительный вал
Решение.
Вал вращается с постоянной угловой скоростью, следовательно, система вращающих моментов уравновешена. Мощность, подводимая к валу без учёта потерь на трение, равна сумме мощностей, снимаемых с вала:
Р1 = Р2 + Р3 + Р4 = 10 + 12 + 8 = 30 кВт.
Определяем вращающий момент на шкивах по формуле:
Момент на шкиве 1 движущий, а моменты на шкивах 2,3,4 – моменты сопротивления механизмов, поэтому они имеют противоположное направление. Брус скручивается между движущим моментом и моментами сопротивления. При равновесии момент движущий равен сумме моментов сопротивления:
m1 = m2 + m3 + m4 = 100 + 120 + 80 =300.
Определяем крутящие моменты в поперечных сечениях бруса с помощью метода сечений.
Мк1 = – m4 = – 80 Н∙м;
Мк2 = – m4 – m3 = – 80 – 120 = – 200 Н∙м;
Мк3 = – m4 – m3 + m1 = – 80 – 120 + 300 = 100 Н∙м;
Мк4 = – m4 – m3 + m1 – m2 = – 80 – 120 + 300 – 100 = 0 Н∙м.
По полученным значениям строим эпюру крутящих моментов (рисунок 2).
Рисунок 2 – Эпюра крутящих моментов
Исходя из условия прочности:
где Мк max – максимальный крутящий момент на валу; Мк max = 200 Н·м;
[τ] – допускаемое касательное напряжение; [τ] = 30 МПа;
WХ – осевой момент сопротивления круглого сечения;
Таким образом
Диаметр вала:
Определяем углы закручивания на каждом участке вала:
где G – модуль упругости сдвига; G = 8·104 МПа.
Jρ – полярный момент инерции; для круга равен
Ответ: φ1 = 0,21º; φ2 = 0,4º; φ3 = 0,33º.
Задания для практической работы.
Исходные данные приведены в таблице 1.
| № варианта | № схемы | Р2, кВт | Р3, кВт | Р4, кВт | ω, рад/с | l1, м | l2, м | l3, м |
| 0,8 | 0,5 | 0,5 | ||||||
| 0,2 | 0,6 | 0,6 | ||||||
| 0,1 | 0,7 | 0,3 | ||||||
| 0,7 | 0,5 | 0,4 | ||||||
| 0,5 | 0,6 | 0,9 | ||||||
| 0,6 | 0,3 | 0,1 | ||||||
| 0,3 | 0,4 | 0,7 | ||||||
| 0,4 | 0,9 | 0,1 | ||||||
| 0,9 | 0,1 | 0,7 | ||||||
| 0,1 | 0,7 | 0,5 | ||||||
| 0,7 | 0,1 | 0,6 | ||||||
| № варианта | № схемы | Р2, кВт | Р3, кВт | Р4, кВт | ω, рад/с | l1, м | l2, м | l3, м |
| 0,5 | 0,7 | 0,4 | ||||||
| 0,6 | 0,5 | 0,9 | ||||||
| 0,7 | 0,6 | 0,1 | ||||||
| 0,5 | 0,7 | 0,7 | ||||||
| 0,6 | 0,5 | 0,5 | ||||||
| 0,3 | 0,6 | 0,6 | ||||||
| 0,4 | 0,7 | 0,7 | ||||||
| 0,9 | 0,4 | 0,5 | ||||||
| 0,1 | 0,9 | 0,6 | ||||||
| 0,7 | 0,1 | 0,3 | ||||||
| 0,1 | 0,7 | 0,4 | ||||||
| 0,7 | 0,5 | 0,4 | ||||||
| 0,5 | 0,6 | 0,9 | ||||||
| 0,6 | 0,7 | 0,1 | ||||||
| 0,7 | 0,5 | 0,7 | ||||||
| 0,5 | 0,6 | 0,1 | ||||||
| 0,6 | 0,3 | 0,7 | ||||||
| 0,7 | 0,4 | 0,5 | ||||||
| 0,5 | 0,9 | 0,6 | ||||||
| 0,6 | 0,7 | 0,7 | ||||||
| 0,3 | 0,4 | 0,5 | ||||||
| 0,4 | 0,9 | 0,6 | ||||||
| 0,9 | 0,1 | 0,7 | ||||||
| 0,1 | 0,7 | 0,5 |
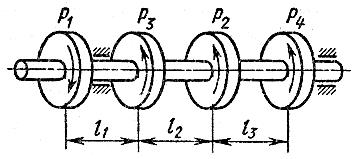 Схема 1
|  Схема 2
|
Схема 3
| 
Схема 4
|
Схема 5
|  Схема 6
|
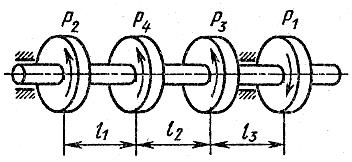Схема 7
| 
Схема 8
|
 Схема 9
| 
Схема 10
|
Поиск по сайту: