 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
РАСЧЕТНЫЕ ЗАДАНИЯ. 1) Векторы. Линейные операции над векторами
ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ
1) Векторы. Линейные операции над векторами.
2) Скалярное произведение, его свойства. Длина вектора. Угол между двумя векторами.
3) Определители, их свойства.
4) Векторное произведение. Свойства. Геометрический смысл.
5) Смешанное произведение, его свойства. Геометрический смысл. Необходимое и достаточное условие компланарности трех векторов.
6) Плоскость. Уравнение плоскости.
7) Расстояние от точки до плоскости.
8) Уравнения прямой в пространстве. Нахождение точки пересечения прямой и плоскости.
ТЕОРЕТИЧЕСКИЕ УПРАЖНЕНИЯ
1) Пусть векторы 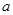 и
и 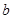 не коллинеарны и
не коллинеарны и  Найти
Найти 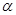 и
и 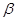 и доказать коллинеарность векторов
и доказать коллинеарность векторов 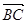 и
и 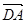 .
.
2) Разложить вектор  по трем некомпланарным векторам
по трем некомпланарным векторам 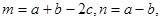
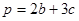 .
.
3) Найти угол между единичными векторами 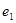 и
и 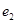 если известно, что векторы
если известно, что векторы 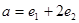 и
и 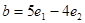 взаимно перпендикулярны.
взаимно перпендикулярны.
4) Доказать компланарность векторов 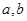 и
и  , зная, что
, зная, что
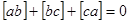 .
.
5) Доказать, что уравнение плоскости, проходящей через точки  и
и 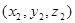 перпендикулярно плоскости
перпендикулярно плоскости 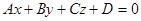 , можно записать в виде
, можно записать в виде
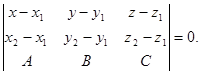
 6) Доказать, что уравнение плоскости, проходящей через пересекающиеся прямые
6) Доказать, что уравнение плоскости, проходящей через пересекающиеся прямые
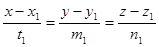 и
и 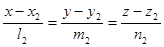 ,
,
можно записать в виде
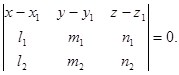
7) Доказать, что уравнения прямой, проходящей через точку  параллельно плоскостям
параллельно плоскостям 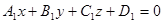 и
и  , можно записать в виде
, можно записать в виде
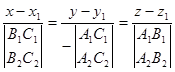
8) Доказать, что необходимым и достаточным условием принадлежности двух прямых
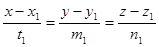 и
и 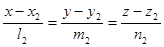 ,
,
одной плоскости является выполнение равенства
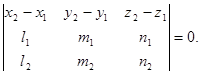
9) Доказать, что расстояние от точки 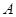 до прямой, проходящей через точку
до прямой, проходящей через точку  и имеющей направляющий вектор
и имеющей направляющий вектор  , определяется формулой
, определяется формулой

10) Даны две скрещивающиеся прямые, проходящие соответственно через точки 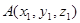 и
и 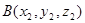 . Их направляющие векторы
. Их направляющие векторы 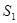 и
и 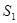 известны. Доказать, что расстояние между ними определяется формулой
известны. Доказать, что расстояние между ними определяется формулой
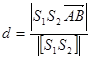 .
.
РАСЧЕТНЫЕ ЗАДАНИЯ
Задача 1. Написать разложение вектора 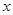 по векторам
по векторам 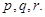
1. 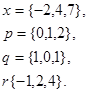
2. 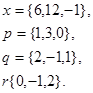
3. 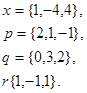
4. 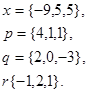
5. 
6. 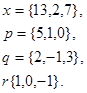
7. 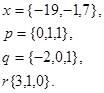
8. 
9. 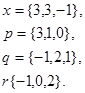
10. 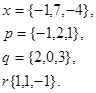
11. 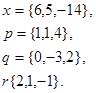
12. 
13. 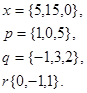
14. 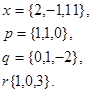
15. 
16. 
17. 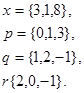
18. 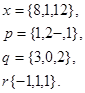
19. 
20. 
21. 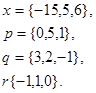
22. 
23. 
24. 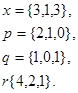
25. 
26. 
27. 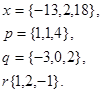
28. 
29. 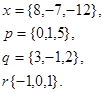
30. 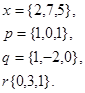
31. 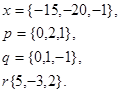
Задача 2. Коллинеарны ли векторы  и
и 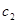 , построенные по векторам
, построенные по векторам 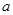 и
и 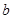 ?
?
1. 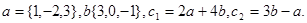
2. 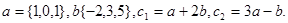
3. 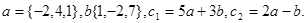
4. 
5. 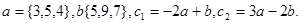
6. 
7. 
8. 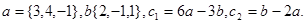
9. 
10. 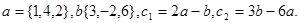
11. 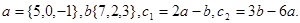
12. 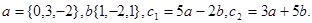
13. 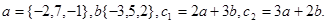
14. 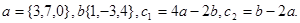
15. 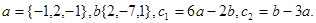
16. 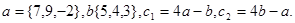
17. 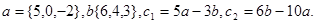
18. 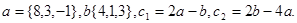
19. 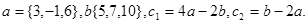
20. 
21. 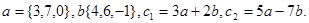
22. 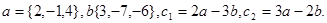
23. 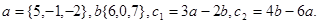
24. 
25. 
26. 
27. 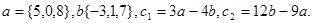
28. 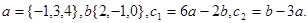
29. 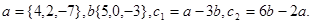
30. 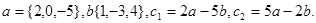
31. 
Задача 3. Найти косинус угла между векторами  и
и 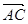 .
.
1. 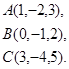
2. 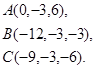
3. 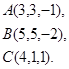
4. 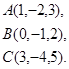
5. 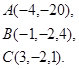
6. 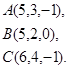
7. 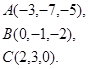
8. 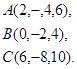
9. 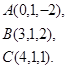
10. 
11. 
12. 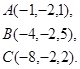
13. 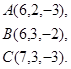
14. 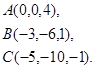
15. 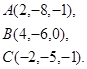
16. 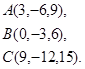
17. 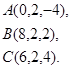
18. 
19. 
20. 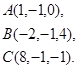
21. 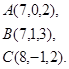
22. 
23. 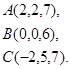
24. 
25. 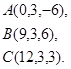
26. 
27. 
28. 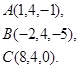
29. 
30. 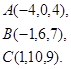
31. 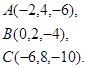
Задача 4. Вычислить площадь параллелограмма, построенного на векторах 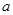 и
и 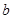 .
.
1. 
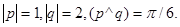
2. 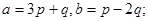
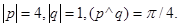
3. 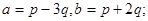
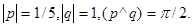
4. 

5. 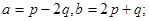
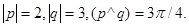
6. 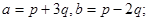
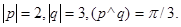
7. 
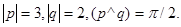
8. 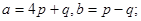
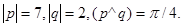
9. 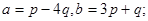
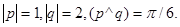
10. 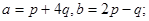
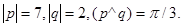
11. 

12. 
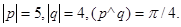
13. 
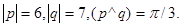
14. 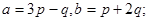

15. 
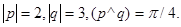
16. 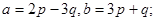

17. 
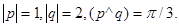
18. 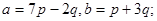
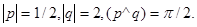
19. 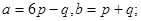
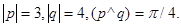
20. 

21. 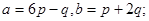
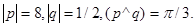
22. 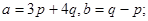
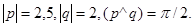
23. 
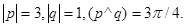
24. 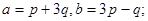
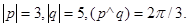
25. 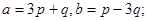
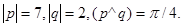
26. 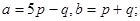

27. 
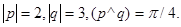
28. 

29. 
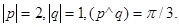
30. 
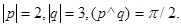
31. 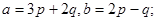
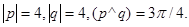
Задача 5. Компланарны ли векторы 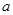 ,
, 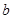 и
и  .
.
1. 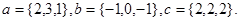
2. 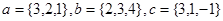
3. 
4. 
5. 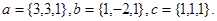
6. 
7. 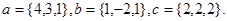
8. 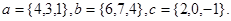
9. 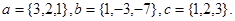
10. 
11. 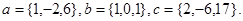
12. 
13. 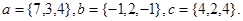
14. 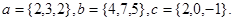
15. 
16. 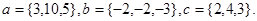
17. 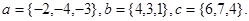
18. 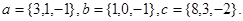
19. 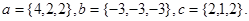
20. 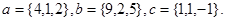
21. 
22. 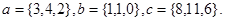
23. 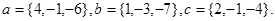
24. 
25. 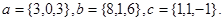
26. 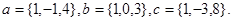
27. 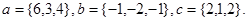
28. 
29. 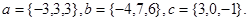
30. 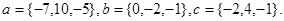
31. 
Задача 6. Вычислить объем тетраэдра с вершинами в точках 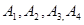 и его высоту, опущенную из вершины
и его высоту, опущенную из вершины 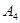 на грань
на грань 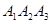 .
.
1. 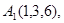
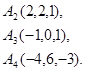
2. 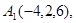
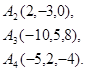
3. 

4. 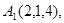
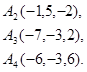
5. 

6. 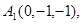
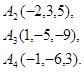
7. 
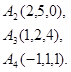
8. 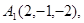
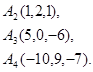
9. 

10. 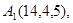
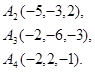
11. 
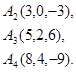
12. 

13. 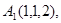
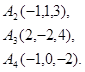
14. 

15. 

16. 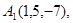

17. 

18. 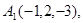
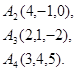
19. 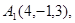
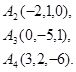
20. 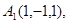
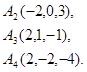
21. 
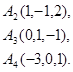
22. 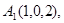
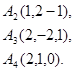
23. 

24. 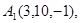

25. 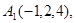
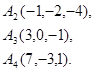
26. 
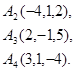
27. 

28. 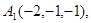

29. 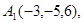
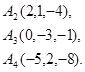
30. 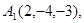
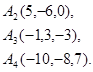
31. 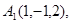
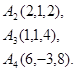
Задача 7. Найти расстояние от точки 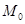 до плоскости, проходящей через точки
до плоскости, проходящей через точки  .
.
1. 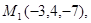

2. 
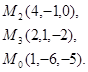
3. 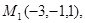
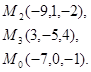
4. 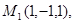

5. 
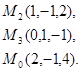
6. 

7. 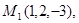
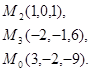
8. 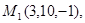

9. 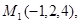
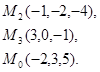
10. 

11. 

12. 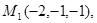

13. 

14. 
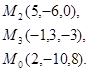
15. 
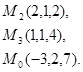
16. 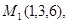

17. 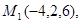

18. 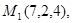
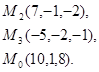
19. 
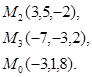
20. 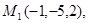
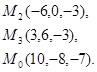
21. 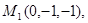

22. 

23. 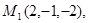
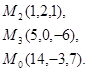
24. 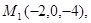
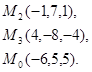
25. 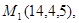

26. 
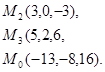 27.
27. 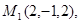

28. 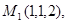
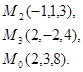
29. 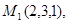
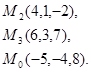
30. 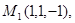
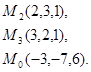
31. 
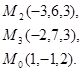
Задача 8. Написать уравнение плоскости, проходящей через точку 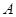 перпендикулярно вектору
перпендикулярно вектору 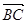 .
.
1. 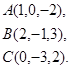
2. 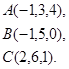
3. 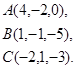
4. 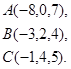
5. 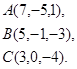
6. 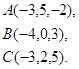
7. 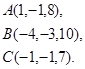
8. 
9. 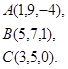
10. 
11. 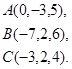
12. 
13. 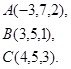
14. 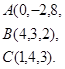
15. 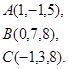
16. 
17. 
18. 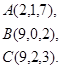
19. 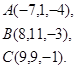
20. 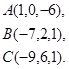
21. 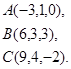
22. 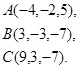
23. 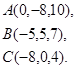
24. 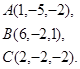
25. 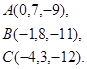
26. 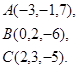
27. 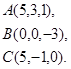
28. 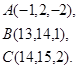
29. 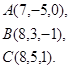
30. 
31. 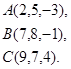
Задача 9. Найти угол между плоскостями.
1. 
2. 
3. 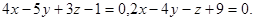
4. 
5. 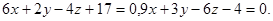
6. 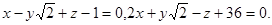
7. 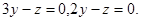
8. 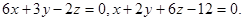
9. 
10. 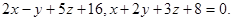
11. 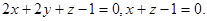
12. 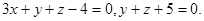
13. 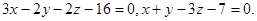
14. 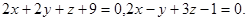
15. 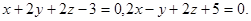
16. 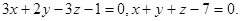
17. 
18. 
19. 
20. 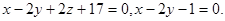
21. 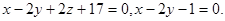
22. 
23. 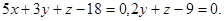
24. 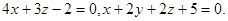
25. 
26. 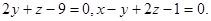
27. 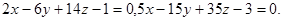
28. 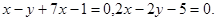
29. 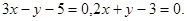
30. 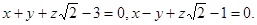
31. 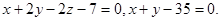
Задача 10. Найти координаты точки 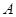 , равноудаленной от точек
, равноудаленной от точек  и
и  .
.
1. 
2. 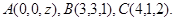
3. 
4. 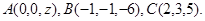
5. 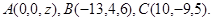
6. 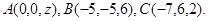
7. 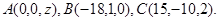
8. 
9. 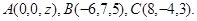
10. 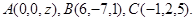
11. 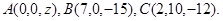
12. 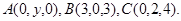
13. 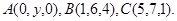
14. 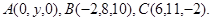
15. 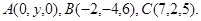
16. 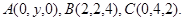
17. 
18. 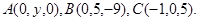
19. 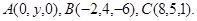
20. 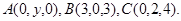
21. 
22. 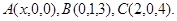
23. 
24. 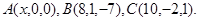
25. 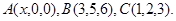
26. 
27. 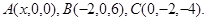
28. 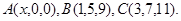
29. 
30. 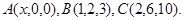
31. 
Задача 11. Пусть 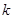 -коэффициент гомотетии с центром в начале координат. Верно ли, что точка
-коэффициент гомотетии с центром в начале координат. Верно ли, что точка 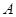 принадлежит образу плоскости
принадлежит образу плоскости 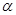 ?
?
1. 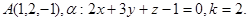
2. 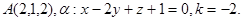
3. 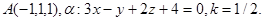
4. 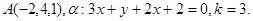
5. 
6. 
7. 
8. 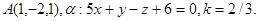
9. 
10. 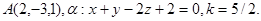
11. 
12. 
13. 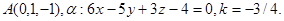
14. 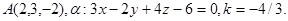
15. 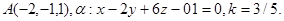
16. 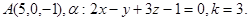
17. 
18. 
19. 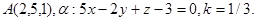
20. 
21. 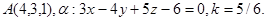
22. 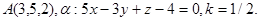
23. 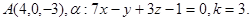
24. 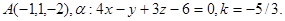
25. 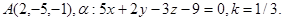
26. 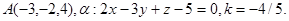
27. 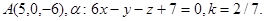
28. 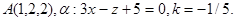
29. 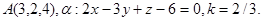
30. 
31. 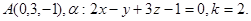
Задача 12. Написать канонические уравнения прямой.
1. 
2. 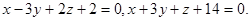
3. 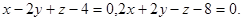
4. 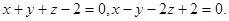
5. 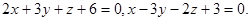
6. 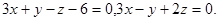
7. 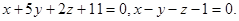
8. 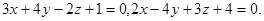
9. 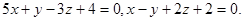
10. 
11. 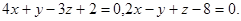
12. 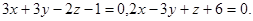
13. 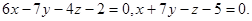
14. 
15. 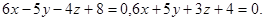
16. 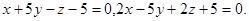
17. 
18. 
19. 
20. 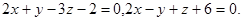
21. 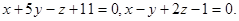
22. 
23. 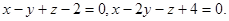
24. 
25. 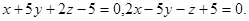
26. 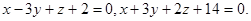
27. 
28. 
29. 
30. 
31. 
Задача 13. Найти точку пересечения прямой и плоскости.
1. 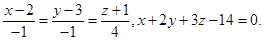
2. 
3. 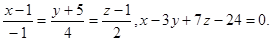
4. 
5. 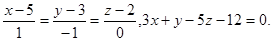
6. 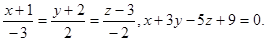
7. 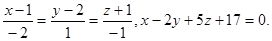
8. 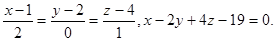
9. 
10. 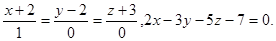
11. 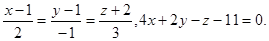
12. 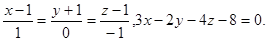
13. 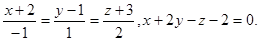
14. 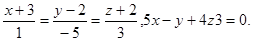
15. 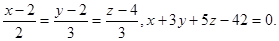
16. 
17. 
18. 
19. 
20. 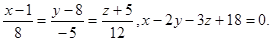
21. 
22. 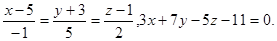
23. 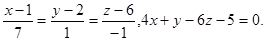
24. 
25. 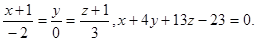
26. 
27. 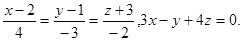
28. 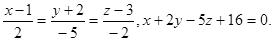
29. 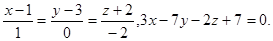
30. 
31. 
Задача 14. Найти точку 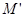 , симметричную точке
, симметричную точке 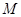 относительно прямой (для вариантов 1-15) или плоскости (для вариантов 16-31).
относительно прямой (для вариантов 1-15) или плоскости (для вариантов 16-31).
1. 
2. 
3. 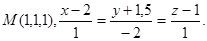
4. 
5. 
6. 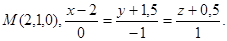
7. 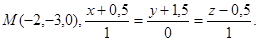
8. 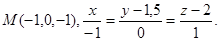
9. 
10. 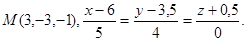
11. 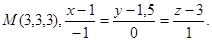
12. 
13. 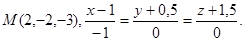
14. 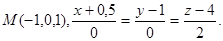
15. 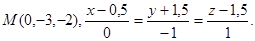
16. 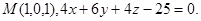
17. 
18. 
19. 
20. 
21. 
22. 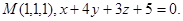
23. 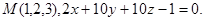
24. 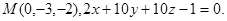
25. 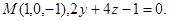
26. 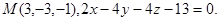
27. 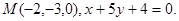
28. 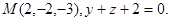
29. 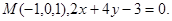
30. 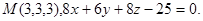
31. 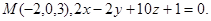
Поиск по сайту: