Непрерывная и дискретная информация

Лекция №1

Тема лекции: Вводная. Основные понятия об информации. Логические и однородные функции.

Содержание (план лекции)

· Непрерывная и дискретная информация.

· Абстрактные алфавиты.

· Слова и абстрактные языки.

· Данные. Типы элементарных данных.

· Логические функции.

· Однородные функции.

Литература по курсу

1. Бардачов Ю.Н., Соколова Н.А., Ходаков В.Е., Основы дискретной математики. Учебное пособие. Под редакц. Ходакова В.Е. – Херсон: из-во ХНТУ, 2000

2. Бардачов Ю.М., Соколова Н.А., Ходаков В.Є. Дискретна математика: Підручник. За ред. В.Є. Ходакова – К.: Вища школа, 2008 – 383 с.

3. Яблонский С.В. Введение в дискретную математику: Учебное пособие для ВУЗов – М.: Наука. – 384 с.

4. Бондаренко М.Ф., Белоус Н.В., Руткас А.Г. Компьютерная дискретная математика – Харьков: «Компания СМИТ», 2004 – 480 с.

5. Акимов О.Е. Дискретная математика: логика, группы, графы, фракталы. – М.: Издатель Акимова, 2005 – 656 с.

6. Тишин В.В. Дискретная математика в примерах и задачах – Санкт – Петербург.: - БВХ – Петербург, 2008 - 352 с.

7. Иванов Б.Н. Дискретная математика. Алгоритмы и программы. Учебное пособие – М.: Лаборатория Базовых Знаний, 2001 – 288 с.

Непрерывная и дискретная информация

Информация о явлениях, процесах представляется с помощью функций

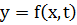
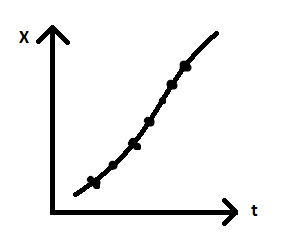
Непрерывное представление информации дискретное представление информации

Любая непрерывная информация может быть апроксимирована дискретной с любой степенью точности

Дискретная форма представления является универсальной.

Результаты измерения скалярных величин могут быть представленны в числовом виде, в виде наборов цифр.

Дискретная форма представления информации отождествляется с цифровой информацией.

Скаляр – величина, каждое значение которой выражается одним действительным числом.

Абстрактные алфавиты

Цифровая информация – частный случай алфавитного представления.

Абстрактный алфавит (алфавит) – конечный набор символов.

Примеры: десятичный алфавит, двоичный, алфавит русского или украинского языков.

Представление одного алфавита средствами другого – кодирование.

Х – алфавит десятичных цифр

У – русский алфавит

кодирование Х в У (10-тичных цифр)

0=а, 1=б, 2=в …. 9=к

Двоичные числа 0v1

N= при n=8 N=256 – достаточно для большинства алфавитов (английский, русский, украинский и т.п.).

Байт – последовательность из 8 двоичных чисел. Байтовый алфавит – 256 букв.

Данные

Данные – информация, с которой имеют дело ЭВМ.

Данные – входные (исходные), промежуточные, выходные.

Данные состоят из составляющих – элементарные данные.

Наиболее употребляемые: целые, вещественные числа, слова, булевы величины.

Булевы величины: 1 – истина

0 – ложь.

Предикат – функция , аргументы которой принадлежат множеству М, Y – истина или нуль (0v1).

Предикат – высказывание описывает свойство, которым обладает или не обладает набор .

При n=2 – предикат «бинарное отношение».

Множество М является алгеброй, если есть аргументы и операции. При n=2 – бинарные операции.

Поиск по сайту: