 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тригонометрическая и показательная формы к.ч
Алгебраическая форма к.ч.
è 
алгебраическая форма к.ч.
Утверждение. Сложение, вычитание, умножение и возведение в натуральную степень к.ч. в алгебраической форме выполняются по правилам действий с алгебраическими двучленами с последующим приведением «подобных слагаемых» и учетом степеней мнимой единицы:
--------------------------------------------------------------------------------------
Формулы «сокращенного умножения: 
----------------------------------------------------------------------------------------
Пример. 
Замечание. Деление к.ч. удобно выполнять, домножив предварительно числитель и знаменатель дроби на к.ч., сопряженное знаменателю:
Пример. 
Модуль и аргумент к.ч. Линии и области на к. плоскости.
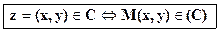
Кроме прямоугольных координат (x,y) точка на комплексной плоскости может быть задана
её радиус-вектором - расстоянием от начала координат 
и «полярным углом» φ – углом между радиус-вектором точки и полуосью X=Re(z)>0: M(x,y) 
M(r,φ), причем
- 
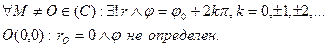
Определение 1.3 Модулемк.ч. z=(x,y) называется неотрицательное (вещественное!) число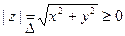 
, равное длине радиус-вектора точки M(x,y) (|z|=r).
Например, 
Определение 2.3 Аргументом к.ч.z=(x,y) называется любой угол Arg(z)=φ, такой, что
Главным значением аргумента к.ч. arg(z)=φ0 называется значение аргумента из интервала [0;2φ) или (-π;π].
Следствия 1.3
1) Arg(z)=arg(z)+2πk,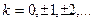 
2) Аргумент к.ч. z=0 не определен.
3) 
| t | 
| 
| 1/2 | -1/2 | -
| -
| -1 | ||
| arccos(t) | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | 5π/6 | π |
4) 
5) Очевидно, что на к. плоскости множеству 
- 
прямая x=a, параллельная оси X=Re(z);
- 
прямая y=а, параллельная оси Y=Im(z);
- 
луч φ=a из начала координат;
- 
окружность радиуса а с центром в начале координат;
- 
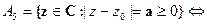окружность радиуса а с центром в точке z0.
ЭКЗ.: Изобразить на к. плоскости множества:
Тригонометрическая и показательная формы к.ч.
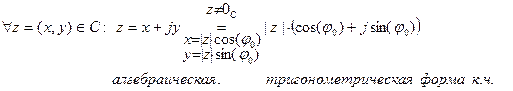
Пример.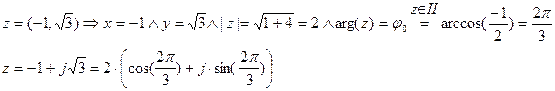 
Утверждение. 
ЭКЗ.: Используя формулу Муавра и условие равенства к. чисел в алгебраической форме, получить триг. формулы для sin(2φ), cos(2φ); sin(3φ), cos(3φ).
Следствия. Действия над к.ч. в показательной форме:
1)Условие равенства к. чисел: 
К. числа равны, если равны их модули, а аргументы отличаются на слагаемое, кратное 2π.
2) при умножении/делении к.ч. их модули перемножаются/делятся, а аргументы складываются/вычитаются:
2) при возведении в степень модуль к.ч. возводится в степень, а аргументумножаетсянапоказатель степени: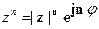 
Примеры.
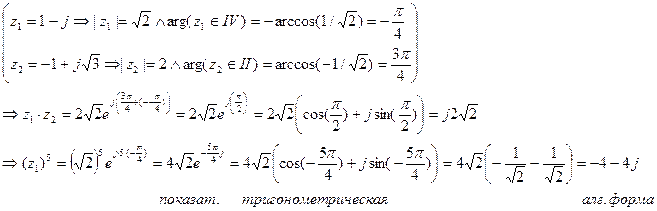
Замечания.
1) Показательная форма к.ч предпочтительна при умножении, делении и возведении к.ч. в степень. Тригонометрическая форма к.ч. удобна для приведения к. числа в показательной форме к алгебраической форме. Алгебраическая форма к.ч. предпочтительна при сложении и вычитании к. чисел.
2) Так как 
, к. число в показательной форме принято приводить к «стандартному виду» 
è 
ЭКЗ. Вычислить и записать три формы к.ч. 
| ТР 2.1 | «Комплексные числа»
Задание. Для заданных к. чисел 
1) Вычислить в алгебраической форме 
2) Записать три формы к. чисел  и изобразить их на комплексной плоскости.
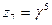3) Вычислить  и записать число  в алгебраической форме.
4) Определить корни полинома  , найти все корни полинома и записать разложение полинома на линейные множители.
5) Определить внутренний и внешний радиусы кольца, заданного неравенством
50.000<|αz+β|<51
|
Поиск по сайту: