Метод усреднения координат

Основы данного метода предлагались многими авторами, в наиболее законченном виде этот метод разрабатывался А.И. Рубаном и его учениками, начиная с 1975 года [12]. Рассмотрим метод более подробно.

Предположим, имеется некоторая вещественная функция одной переменной в ограниченной области евклидова пространства . Данная функция ограничена и непрерывна почти всюду на . Область состоит из конечного или счетного множества замкнутых ограниченных непересекающихся подобластей, в каждой из которых функция ограничена и непрерывна. Примером служат ограниченные на замкнутом интервале функции, имеющие конечное или счетное множество точек разрыва первого рода. Точки разрыва делят интервал на конечное или счетное множество подынтервалов, в каждом из которых функция непрерывна.

Необходимо найти в глобальный экстремум:

- минимум при ;

- максимум при ,

функции при условии его единственности. Глобальный экстремум может находиться внутри области и на ее границе.

Вводим последовательность непрерывных, положительных в функций при , таких, что для любых (где ) последовательность с ростом монотонно нарастает, таким образом, что

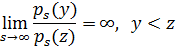
При выполнении указанных условий справедлив результат:

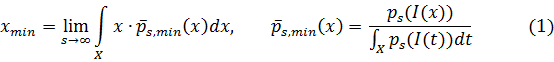
Каждую нормированную на единицу весовую функцию можно мыслить как плотность распределения вероятности непрерывной случайной величины, изменяющейся в области . Тогда в правой части формулы расчета 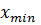стоит предел последовательности математических ожиданий от . С ростом плотности распределения при трансформируются так, что в пределе выделяют рассматриваемую функцию в точке глобального минимума . Таким образом, в пределе последовательность выходит к многомерной дельта функции с точкой локализации .

Для точки глобального максимума: при – справедливо равенство

аналогичное вышеприведенному с заменой на .

Считаем, что известны точная верхняя при и точная нижняя при границы рассматриваемой функции . Для удобства расчета и повышения точности вычислений в (1) и (2) используем нормированные неотрицательные переменные , лежащие в интервале [0; 1]:

Таким образом, метод усреднения координат основан на случайном просмотре области поиска экстремума и усреднении полученных значений, на основании которого происходит последовательное приближение к экстремуму.

Поиск по сайту: