Операції на множинах

Лекція 2

Тема: Геометрична інтерпритація множин. Операції на множинах

Геометрична інтерпритація множин.

Для наглядного зображення співвідношень між підмножинами універсальної множини використовуються діаграми Венна і круги Ейлера.

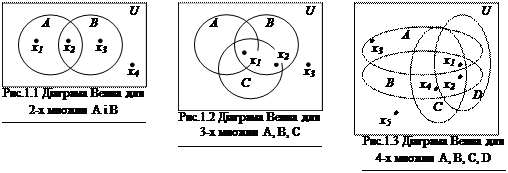
Побудова діаграми Венна полягає в розбитті площини на 2ⁿ областей за допомогою n фігур. Кожна фігура на діаграмі зображує окрему множину, n – число зображуваних множин. При цьому кожна наступна фігура повинна мати одну і тільки одну загальну область-перетин з кожною з раніш побудованих фігур. Площина, на якій зображуються фігури, становить універсальну множину U. Таким чином, точки, що не належать жодній з фігур, належать тільки U. Діаграма Венна для двох множин А і В зображена на малюнку 1.1.

За допомогою діаграм Венна можна графічно показати, чи належить деякий елемент певній множині. Наприклад, на рис.1.1 елемент х₁ÎА, х₁ÏВ, а елемент х₁ÎА, х₁ÎВ. На рис.1.2 зображено 2 множини, і видно, що елемент х₁ÎА, х₁ÎВ, х₁ÎС, а елемент х₂ÏА, х₂ÎВ, х₂ÎС. Елемент х₃ÏА, х₃ÏВ, х₃ÏС.

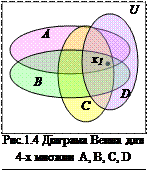
На рис.1.4 зображено 4 множини. Кожну множину для більш явного уявлення можна зображувати забарвленими різними кольорами.

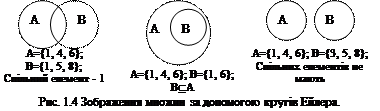Діаграми Венна не відображають реальні відношення включення, що встановлені між множинами, а розглядають їх в загальному випадку. Індивідуальні відношення між заданими множинами зображують за допомогою кругів Ейлера. В цьому випадку множини, що не мають спільних елементів, зображують не перетин ними фігурами. Відношення включення на множи-нах зображують, роз-ташовуючи їх вкладе-ними одна в одну. Розглянемо на рис.1.4 круги Ейлера.

Операції на множинах

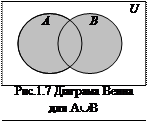Для наочного зображення операцій будемо використовувати діаграми Венна, в яких круги зображують множини, що беруть участь в операції, а заштрихована область – результат операції.

1. Об’єднання (сума) АÈВ є множина, що складається з тих і тільки тих елементів, які входять або до А, або до В, або до А і В одночасно.

Приклад. Нехай дані множини A={a,b,m}, B={m,c,p}, тоді АÈВ={a,b,m,c,p}.

2. Перетин (добуток) АÇВ є множина, що містить тільки елементи, які належать А і В одночасно. (рис.1.8)

Приклад. Нехай дані множини A={a,b,m}, B={m,c,p}, тоді АÇВ={m}.

3. Різниця А\ В є множина, що складається в точності з усіж елементів А, які не належать до В. (рис.1.9)

Приклад. Нехай дані множини A={a,b,m}, B={m,c,p}, тоді А\ В={a,b}.

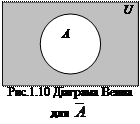Доповнення (заперечення) 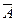(читається «не А») є множина U\ A. (рис.1.10).

Приклад. Якщо універсалом U визначити всю множину натуральних чисел, а множина А – множина парних чисел, то 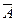- множина непарних чисел.

Запитання

1. В чому відмінність між діаграмами Венна і кругами Ейлера?

2. Як розташовані круги Ейлера для множин, які не мають спільних точок, мають спільні точки?

3. Як за допомогою кругів Ейлера зобразити підмножини даної множини?

4. Дайте визначення операціям на множинах.

5. Наведіть самостійно приклади множин і виконайте кожну з чотирьох операцій.

6. При виконанні якої операції використовується універсальна множина?

7. Чи можуть деякі з операцій бути виражені одна через іншу? Яким чином?

Поиск по сайту: