 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Часть 1. Теоретические основы теории кодирования
Полная версия.
Кодирование информации.
Постановка проблемы.
Что такое кодирование информации? Для чего оно необходимо?
Как сжать текст, сохранив возможность его реконструкции?
В каком порядке целесообразно размещать слова в словаре или в памяти компьютера?
Как работают такие популярные программы сжатия информации как PKZIP, ARJ, LHA, STACKER, SuperStor? Какие алгоритмы сжатия информации лежат в основе их работы?
В чем смысл магической формулы:
СЖАТИЕ = МОДЕЛИРОВАНИЕ + КОДИРОВАНИЕ?
Что такое шифрование?
Примеры кодирования.
1. Кодирование чисел:
- Десятичная система счисления;
- Римские цифры;
- Кодирование чисел в памяти компьютера - типы: byte, integer, longint, real.
2. Кодирования геометрических объектов формулами - Декартовы координаты.
3. Кодирование текстовой информации:
- Азбука Морзе.
Азбука Морзе — это схема алфавитного кодирования, где по историческим и техническим причинам 0 называется точкой и обозначается знаком «•», а 1 называется тире и обозначается знаком «-». Непосредственно проверяется, что неравенство Макмиллана(см.ниже) для азбуки Морзе не выполнено, и, следовательно, эта схема не является разделимой. На самом деле в процессе передачи информации с использованием азбуки Морзе имеются дополнительные элементы — паузы между буквами (и словами), которые позволяют декодировать сообщения. Эти дополнительные элементы определены неформально, поэтому прием и передача сообщений с помощью азбуки Морзе, особенно с высокой скоростью, является некоторым искусством, а не простой технической процедурой.
Схема кодирования Морзе:
| Символ | Код | Символ | Код | Символ | Код | Символ | Код | Символ | Код | |||||
| А | .- | Л | .-.. | Ц | -.-. | .---- | . | ...... | ||||||
| Б | -... | М | -- | Ч | ---. | ..--- | , | .-.-.- | ||||||
| В | .-- | Н | -. | Ш | ---- | ...-- | ; | -.-.-. | ||||||
| Г | --. | О | --- | Щ | --.- | ....- | : | ... | ||||||
| Д | -.. | П | .--. | Ы | -.-- | ..... | ? | ..--.. | ||||||
| Е | . | Р | .-. | Ь,Ъ | -..- | -.... | ! | --..-- | ||||||
| Ж | ...- | С | ... | Э | ..-.. | --... | () | -.--.- | ||||||
| З | --.. | Т | - | Ю | ..-- | ---.. | / | ------ | ||||||
| И | .. | У | ..- | Я | .-.- | ----. | ||||||||
| Й | .--- | Ф | ..-. | ----- | ||||||||||
| К | -.- | Х | .... |
| Вступление в pаботу (сеpия букв ЖЖ) | ...-...-...- | Знак конца (ЕЦ) | .-.-. |
| Начало пеpедачи | -.-.- | Полный конец (СК) | ...-.- |
| Знак pаздела | -...- | Номеp (pаздельно НР) | -..-. |
| Знак ошибки (сеpия pаздельных точек) | ...... | "Ждать" | .-... |
- таблица АSCII.
Стандартная таблица ASCII (десятичные коды символов 0 - 127)
┌────────────┬────────────┬────────┬───────┬───────┬───────┬───────┬───────┐
| 000 (nul) | 016 (dle) | 032 sp | 048 0 | 064 @ | 080 P | 096 ` | 112 p |
| 001 (soh) | 017 (dc1) | 033! | 049 1 | 065 A | 081 Q | 097 a | 113 q |
| 002 (stx) | 018 (dc2) | 034 " | 050 2 | 066 B | 082 R | 098 b | 114 r |
| 003 (etx) | 019 (dc3) | 035 # | 051 3 | 067 C | 083 S | 099 c | 115 s |
| 004 (eot) | 020 (dc4) | 036 $ | 052 4 | 068 D | 084 T | 100 d | 116 t |
| 005 (enq) | 021 (nak) | 037 % | 053 5 | 069 E | 085 U | 101 e | 117 u |
| 006 (ack) | 022 (syn) | 038 & | 054 6 | 070 F | 086 V | 102 f | 118 v |
| 007 (bel) | 023 (etb) | 039 ' | 055 7 | 071 G | 087 W | 103 g | 119 w |
| 008 (bs) | 024 (can) | 040 (| 056 8 | 072 H | 088 X | 104 h | 120 x |
| 009 (tab) | 025 (em) | 041) | 057 9 | 073 I | 089 Y | 105 i | 121 y |
| 010 (lf) | 026 (eof) | 042 * | 058: | 074 J | 090 Z | 106 j | 122 z |
| 011 (vt) | 027 (esc) | 043 + | 059; | 075 K | 091 [ | 107 k | 123 { |
| 012 (np) | 028 (fs) | 044, | 060 < | 076 L | 092 \ | 108 l | 124 | |
| 013 (cr) | 029 (gs) | 045 - | 061 = | 077 M | 093 ] | 109 m | 125 } |
| 014 (so) | 030 (rs) | 046. | 062 > | 078 N | 094 ^ | 110 n | 126 ~ |
| 015 (si) | 031 (us) | 047 / | 063? | 079 O | 095 _ | 111 o | 127 |
└────────────┴────────────┴────────┴───────┴───────┴───────┴───────┴───────┘
Расширенная таблица ASCII (десятичные коды символов 128 - 255)
┌─────────┬───────┬───────┬───────┬────---┬────---┬───────┬───────┬─────────┐
| 128 А | 143 П | 158 Ю | 172 м | 186 ║ | 200 ╚ | 214 ╓ | 228 ф | 242 Є |
| 129 Б | 144 Р | 159 Я | 173 н | 187 ╗ | 201 ╔ | 215 ╫ | 229 х | 243 є |
| 130 В | 145 С | 160 а | 174 о | 188 ╝ | 202 ╩ | 216 ╪ | 230 ц | 244 Ї |
| 131 Г | 146 Т | 161 б | 175 п | 189 ╜ | 203 ╦ | 217 ┘ | 231 ч | 245 ї |
| 132 Д | 147 У | 162 в | 176 ░ | 190 ╛ | 204 ╠ | 218 ┌ | 232 ш | 246 Ў |
| 133 Е | 148 Ф | 163 г | 177 ▒ | 191 ┐ | 205 ═ | 219 █ | 233 щ | 247 ў |
| 134 Ж | 149 Х | 164 д | 178 ▓ | 192 └ | 206 ╬ | 220 ▄ | 234 ъ | 248 ° |
| 135 З | 150 Ц | 165 е | 179 | | 193 ┴ | 207 ╧ | 221 ▌ | 235 ы | 249 ∙ |
| 136 И | 151 Ч | 166 ж | 180 ┤ | 194 ┬ | 208 ╨ | 222 ▐ | 236 ь | 250 · |
| 137 Й | 152 Ш | 167 з | 181 ╡ | 195 ├ | 209 ╤ | 223 ▀ | 237 э | 251 √ |
| 138 К | 153 Щ | 168 и | 182 ╢ | 196 ─ | 210 ╥ | 224 р | 238 ю | 252 № |
| 139 Л | 154 Ъ | 169 й | 183 ╖ | 197 ┼ | 211 ╙ | 225 с | 239 я | 253 ¤ |
| 140 М | 155 Ы | 170 к | 184 ╕ | 198 ╞ | 212 ╘ | 226 т | 240 Ё | 254 ■ |
| 141 Н | 156 Ь | 171 л | 185 ╣ | 199 ╟ | 213 ╒ | 227 у | 241 ё | 255 |
| 142 О | 157 Э | | | | | | | |
└─────────┴───────┴───────┴───────┴───────┴───────┴───────┴───────┴─────────┘
Задачи, решаемые посредством кодирования:
1. Представление данных(приспособление формы данных к конкретному каналу связи или какому-либо другому устройству, предназначенному для преобразования или хранения информации).
2. Защита информации от несанкционированного доступа.
3. Обеспечение помехоустойчивости при передаче данных по каналам связи.
4. Сжатие информации.
5. Трансляция и компиляция кода программ.
Часть 1. Теоретические основы теории кодирования.
$0. Необходимые минимальные знания.
$0.1. Двоичная арифметика.
Двоичные коды чисел, перевод записи чисел из десятичной в двоичную и обратно, арифметические действия над двоичными числами.
$0.2. Элементы теории графов.
Граф. Ориентированный и неориентированный граф. Путь в графе. Связность. Циклы. Деревья. Бинарный граф. Бинарное дерево. Соотношение префиксный код <-> листья бинарного дерева.
Отступление.
Классическими в теории графов являются следующие задачи.
1. Задача о кенигсбергских мостах. Имеются два острова, соединенных семью мостами с берегами реки и друг с другом (рис.3). Задача состоит в следующем: осуществить прогулку по городу таким образом, чтобы, пройдя по каждому мосту один раз, вернуться обратно. Решение этой задачи сводиться к нахождению некоторого специального маршрута на графе.
С

Рис.3. План расположения мостов и соответствующий ему граф.
Вершины С, В соответствуют правому и левому берегам реки, А и D - островам, ребра графа - мосты. На языке графов, задача формулируется следующим образом: существует ли в графе простой цикл, содержащий все ребра (эйлеров цикл).
2. Задача о трех колодцах. На участке 3 дома и 3 колодца. От каждого дома к каждому колодцу ведет тропинка (см. соответствующий граф рис. 4). Когда владельцы домов поссорились, они задумали проложить дороги от каждого дома к каждому колодцу так, чтобы не встречаться на пути к колодцам.
Покажите, что их намерения не могли осуществиться.
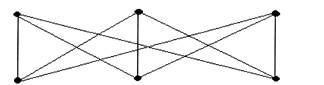
Рис.4
Определение. Граф - это набор точек на плоскости (эти точки называются вершинами графа), некоторые из которых соединены отрезками (эти отрезки называются ребрами графа).
Определение. Говорят, что две вершины графа соединены путем, если из одной вершины можно пройти по ребрам в другую вершину.
Путей между двумя данными вершинами может быть несколько. Поэтому обычно путь обозначают перечислением вершин, которые посещаются при движении по ребрам.
Определение. Граф называется связным, если любые две его вершины соединены некоторым путем.
На рис.5 и рис.6 приведены примеры несвязного и связного графов соответственно.
Определение. Состоящий из различных ребер замкнутый путь называется циклом. Определение. Связный граф, в котором нет циклов, называется деревом.
Пример дерева дан на рис. 2. Одним из основных отличительных свойств дерева является то, что в нем любые две вершины соединены единственным путем.
Определение. Дерево называется ориентированным, если на каждом его ребре указано направление.
Следовательно, о каждой вершине ориентированного дерева можно сказать, какие ребра в нее входят, какие выходят. Точно так же о каждом ребре можно сказать, из какой вершины оно выходит и в какую входит.
Определение. Двоичное дерево - это такое ориентированное дерево, в котором:
1) имеется ровно одна вершина, в которую не входит ни одного ребра(эта вершина называется корнем двоичного дерева);
2) в каждую вершину, кроме корня, входит одно ребро;
3) из каждой вершины (включая корень) исходит не более двух ребер
$1.1. Понятие кодирования. Формализация кодирования.
Пусть A={ a1, a2, …, an} - конечное упорядоченное множество символов, называемое алфавитом. Под словом в алфавите A будем понимать любую конечную последовательность символов из A. Длиной слова назовем количество букв его составляющих.
Обозначим через A* - множество слов в алфавите A.
Кодом назовем любую конечную совокупность слов {x1, x2,..., xk} в некотором алфавите A.
Определение. Кодирование - операция отождествления символов или групп символов одного кода с символами или группами символов другого кода.
Пример. Арабская запись целых чисел à формат integer.
Необходимость кодирования возникает прежде всего из потребности приспособить форму сообщения к данному каналу связи или какому-либо другому устройству, предназначенному для преобразования или хранения информации. Так, с помощью телеграфных кодов сообщения, представленные в виде последовательности букв, например, русского языка, и цифр, преобразуются в определенные комбинации посылок тока.
Задание. Разбить группу на пары. Обменяться закодированными с помощью таблицы А8СП текстами:
1. Неравенство_Макмиллана
2. Левенштейна_кодирование
3. Полиноминальное_хеширование
4. Источники_c_избыточностью
5. Арифметические_коды_Риссанена
6. Результаты_Зива_Лемпеля
Поиск по сайту: