Ограничения пучков лучей

Основы оптики

Все оптические явления, в том числе и формирование изображения в микроскопе, изучает оптика - учение о физических явлениях, связанных с распространением и взаимодействием с веществом электромагнитных волн, длина которых лежит в интервале 10^-4 - 10^-9 м.

На рис. 5. показан участок шкалы электромагнитного излучения в длинах волн, соответствующий оптическому диапазону. Границы оптического диапазона, а также границы между его участками установлены на основе экспериментальных данных и не являются абсолютно точными.

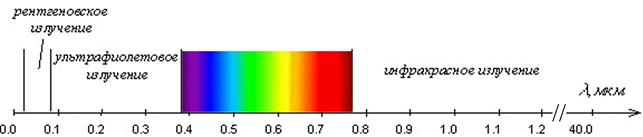
Рис. 5. Оптический диапазон.

Большое значение этой области спектра электромагнитных волн для практической деятельности человека обусловлено прежде всего тем, что внутри нее в узком интервале длин волн от 0,4 до 0,7 мкм лежит участок видимого света, непосредственно воспринимаемого человеческим глазом (рис.6).

Для частот, более низких, чем частоты оптического диапазона, нельзя построить оптические системы по законам геометрической оптики, а электромагнитное излучение более высоких частот, как правило, либо проходит сквозь любое вещество, либо разрушает его.

Специфика оптического диапазона заключается в его двух главных особенностях:

- в оптическом диапазоне выполняются законы геометрической оптики,

- в оптическом диапазоне свет очень слабо взаимодействует с веществом.

Наиболее полное представление о формировании изображения дает т.н. геометрическая оптика, которая основывается на представлении о прямолинейном распространении света. Геометрическая оптика, отвлекаясь от волновой природы света, описывает его распространение с помощью лучей.

И сейчас попытаемся разобрать основные положения геометрической оптики

Луч - это прямая или кривая линия, вдоль которой распространяется энергия светового поля. В волновой оптике световой луч совпадает с направлением нормали к волновому фронту, а в корпускулярной – с траекторией движения частицы. В случае точечного источника в однородной среде световые лучи представляют собой прямые линии, выходящие из источника во всех направлениях. На границах раздела однородных сред направление световых лучей может изменяться вследствие отражения или преломления, но в каждой из сред они остаются прямыми. Также в соответствии с опытом принимается, что при этом направление световых лучей не зависит от интенсивности света.

Отражение.

Когда свет отражается от полированной плоской поверхности, угол падения (измеренный от нормали к поверхности) равен углу отражения (рис. 7), причем отраженный луч, нормаль и падающий луч лежат в одной плоскости. Если на плоское зеркало падает световой пучок, то при отражении форма пучка не изменяется; он лишь распространяется в другом направлении. Поэтому, глядя в зеркало, можно видеть изображение источника света (или освещенного предмета), причем изображение кажется таким же, как и исходный объект, но находящимся за зеркалом на расстоянии, равном расстоянию от объекта до зеркала. Прямая, проходящая через точечный объект и его изображение, перпендикулярна зеркалу.

Отражение от кривых поверхностей происходит по тем же законам, что и от прямых, причем нормаль в точке отражения проводится перпендикулярно касательной плоскости в этой точке. Простейший, но самый важный случай – отражение от сферических поверхностей. В этом случае нормали совпадают с радиусами. Здесь возможны два варианта:

1. Вогнутые зеркала: свет падает изнутри на поверхность сферы. Когда пучок параллельных лучей падает на вогнутое зеркало (рис. 8, а), отраженные лучи пересекаются в точке, расположенной на половине расстояния между зеркалом и центром его кривизны. Эта точка называется фокусом зеркала, а расстояние между зеркалом и этой точкой – фокусным расстоянием. Расстояние s от объекта до зеркала, расстояние s  от зеркала до изображения и фокусное расстояние f связаны формулой 1/ f = (1/ s) + (1/ s ), где все величины следует считать положительными, если их измерять влево от зеркала, как на рис. 9, а. Когда объект находится на расстоянии, превышающем фокусное, формируется действительное изображение, но когда расстояние s меньше фокусного расстояния, расстояние до изображения s  становится отрицательным. При этом изображение формируется за зеркалом и является мнимым.

На рис. 9, а показано вогнутое зеркало. Слева в виде вертикальной стрелки изображен объект высотой h. Радиус сферического зеркала равен R, а фокусное расстояние f = R /2. В этом примере расстояние s от зеркала до объекта больше R. Изображение можно построить графически, если из бесконечно большого числа световых лучей рассмотреть три, исходящие из вершины объекта. Луч, параллельный главной оптической оси, после отражения от зеркала пройдет через фокус. Второй луч, попадающий в центр зеркала, отразится таким образом, что падающий и отраженный лучи образуют одинаковые углы с главной осью. Пересечение этих отраженных лучей даст изображение верхней точки объекта, а полное изображение объекта можно получить, если из этой точки опустить перпендикуляр h  на главную оптическую ось. Для проверки можно проследить за ходом третьего луча, идущего через центр кривизны зеркала и отражающегося от него обратно по тому же самому пути. Как видно из рисунка, он тоже пройдет через точку пересечения первых двух отраженных лучей. Изображение в этом случае будет действительным (оно формируется настоящими световыми пучками), перевернутым и уменьшенным.

То же самое зеркало представлено на рис. 9, б, но расстояние до объекта меньше фокусного. В этом случае после отражения лучи образуют расходящийся пучок, а их продолжения пересекаются в точке, которую можно рассматривать как источник, из которого выходит весь пучок. Изображение будет мнимым, увеличенным и прямым.

Преломление.

При прохождении света через границу раздела двух прозрачных сред, таких, как воздух и стекло, угол преломления (между лучом во второй среде и нормалью) меньше угла падения (между падающим лучом и той же нормалью), если свет проходит из воздуха в стекло (рис.10), и больше угла падения, если свет проходит из стекла в воздух. Преломление подчиняется закону Снеллиуса, согласно которому падающий и преломленный лучи и нормаль, проведенная через точку пересечения светом границы сред, лежат в одной плоскости, а угол падения i и угол преломления r, отсчитываемые от нормали, связаны соотношением n = sin i /sin r, где n – относительный показатель преломления сред, равный отношению скоростей света в этих двух средах (скорость света в стекле меньше, чем в воздухе).

Если свет проходит через плоскопараллельную стеклянную пластинку, то, поскольку такое двукратное преломление симметрично, выходящий луч параллелен падающему. Если свет падает не по нормали к пластинке, то выходящий луч будет смещен относительно падающего на расстояние, зависящее от угла падения, толщины пластинки и показателя преломления.

Если же пучок света проходит через призму (рис. 11), то направление выходящего пучка изменяется.

Кроме того, показатель преломления стекла неодинаков для разных длин волн: для фиолетового света он больше, чем для красного. Поэтому, когда через призму проходит белый свет, его цветовые составляющие отклоняются в разной степени, разлагаясь в спектр. Менее всего отклоняется красный свет, за ним следуют оранжевый, желтый, зеленый, голубой, синий и, наконец, фиолетовый. Зависимость показателя преломления от длины волны излучения называется дисперсией. Дисперсия, как и показатель преломления, сильно зависит от свойств материала. Угловое отклонение D (рис. 11) минимально при симметричном ходе луча через призму, когда угол падения луча при входе в призму равен углу, под которым этот луч выходит из призмы. Такой угол называется углом минимального отклонения. Для призмы с преломляющим углом A (углом при вершине) и относительным показателем преломления n справедливо соотношение n = sin[(A + D)/2]sin(A /2), которым определяется угол минимального отклонения.

Критический угол. Когда луч света переходит из оптически более плотной среды, такой, как стекло, в менее плотную, такую, как воздух, угол преломления оказывается больше угла падения (рис. 12). При некотором значении угла падения, которое называется критическим, преломленный луч будет скользить вдоль границы раздела, все еще оставаясь во второй среде. Когда угол падения превысит критический, преломленного луча уже не будет, а свет полностью отразится назад в первую среду. Такое явление называется полным внутренним отражением. Поскольку при угле падения, равном критическому, угол преломления равен 90 (sin r = 1), критический угол C, при котором начинается полное внутреннее отражение, дается соотношением sin C = 1/ n, где n – относительный показатель преломления.

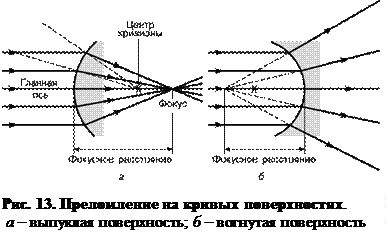Линзы. При преломлении на кривых поверхностях тоже применим закон Снеллиуса, как и закон отражения. Опять-таки наиболее важное значение имеет случай преломления на сферической поверхности. Рассмотрим рис. 13, а. Прямая, проведенная через вершину сферического сегмента и центр кривизны, называется главной осью. Луч света, идущий вдоль главной оси, падает на стекло по нормали и потому проходит без изменения направления, но другие, параллельные ему лучи падают на поверхность под разными углами к нормали, увеличивающимися с удалением от главной оси. Поэтому и преломление будет больше для удаленных лучей, но все лучи такого параллельного пучка, идущего параллельно главной оси, пересекут ее в точке, называемой главным фокусом. Расстояние от этой точки до вершины поверхности называется фокусным расстоянием.

Если пучок таких же параллельных лучей падает на вогнутую поверхность, то после преломления пучок становится расходящимся, а продолжения этих лучей пересекаются в точке, которая называется мнимым фокусом (рис. 13, б). Расстояние от этой точки до вершины тоже называется фокусным расстоянием, но ему приписывается знак «минус».

Тело из стекла или другого оптического материала, ограниченное двумя поверхностями, радиусы кривизны и фокусные расстояния которых велики по сравнению с другими размерами, называется тонкой линзой. Из шести линз, показанных на рис. 14, первые три – собирающие, а остальные три – рассеивающие. Фокусное расстояние тонкой линзы можно рассчитать, если известны радиусы кривизны и показатель преломления материала. Соответствующая формула имеет вид где R ₁ и R ₂ – радиусы кривизны поверхностей, которые в случае двояковыпуклой линзы (рис. 15) считаются положительными, а в случае двояковогнутой – отрицательными.

Положение изображения для заданного объекта можно рассчитать по простой формуле с учетом некоторых условностей, показанных на рис. 15. Объект помещают слева от линзы, а ее центр считается началом координат, от которого измеряются все расстояния вдоль главной оси. Область слева от линзы называется пространством объекта, а справа – пространством изображения.

При этом расстояние до объекта в пространстве объекта и расстояние до изображения в пространстве изображения считаются положительными. Все расстояния, показанные на рис. 15, положительные.

В этом случае, если f – фокусное расстояние, s – расстояние до объекта, а s  – расстояние до изображения, формула тонкой линзы запишется в виде 1/ f = (1/ s) + (1/ s ).

Руководствуясь рис. 15, можно построить также изображение точек, находящихся вне главной оси. Плоскому объекту, перпендикулярному оси, будет соответствовать также плоское и перпендикулярное оси изображение при условии, что размеры объекта малы по сравнению с фокусным расстоянием. Лучи, проходящие через центр линзы, не отклоняются, а лучи, параллельные главной оси, пересекаются в фокусе, лежащем на этой оси. Объект на рис. 15 представлен стрелкой h слева. Изображение верхней точки объекта находится в точке пересечения множества исходящих из нее лучей, из которых достаточно выбрать два: луч, параллельный главной оси, который затем пройдет через фокус, и луч, проходящий через центр линзы, который не меняет своего направления, проходя через линзу. Получив таким образом верхнюю точку изображения, достаточно опустить перпендикуляр на главную ось, чтобы получить все изображение, высоту которого обозначим через h . В случае, показанном на рис. 15, мы имеем действительное, перевернутое и уменьшенное изображение. Из соотношений подобия треугольников нетрудно найти отношение m высоты изображения к высоте объекта, которое называется увеличением:

m = h / h = s / s.

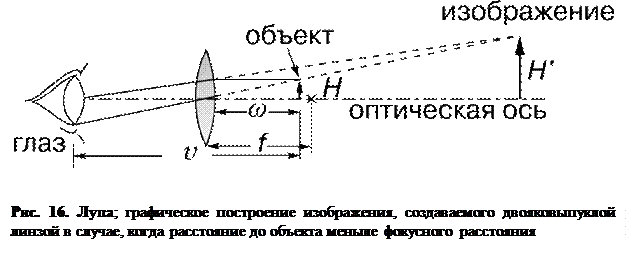
Если рассматривать через эту линзу предмет, расположенный за линзой не дальше ее фоукуса, то видно увеличенное мнимое изображение предмета. Такая линза представляет собой простейший микроскоп и называется лупой или увеличительным стеклом. Из схемы рис. 16 можно определить размер увеличенного изображения.

Когда глаз настроен на параллельный пучок света (изображение предмета находится на неопределенно большом расстоянии, а это означает, что предмет расположен в фокальной плоскости линзы), видимое увеличение M можно определить из соотношения (рис. 16): M = tg  /tg  = (H / f)/(H / v) = v / f, где f – фокусное расстояние линзы, v – расстояние наилучшего зрения, т.е. наименьшее расстояние, на котором глаз хорошо видит при нормальной аккомодации. M увеличивается на единицу, когда глаз настраивается так, что мнимое изображение предмета оказывается на расстоянии наилучшего зрения. Способности к аккомодации у всех людей разные, с возрастом они ухудшаются; принято считать 25 см расстоянием наилучшего зрения нормального глаза. В поле зрения одиночной положительной линзы при удалении от ее оси резкость изображения быстро ухудшается из-за поперечных аберраций. Хотя и бывают лупы с увеличением в 20 крат, типичная их кратность от 5 до 10. Увеличение сложного микроскопа, состоящего из нескольких линз, именуемого обычно просто микроскопом, доходит до 1500-2000 крат.

Комбинации линз. Когда речь идет о системе нескольких линз, положение окончательного изображения определяется последовательным применением к каждой линзе известной нам формулы с учетом знаков. Такую систему можно заменить одной линзой с «эквивалентным» фокусным расстоянием. В случае двух отстоящих друг от друга на расстояние a простых линз с общей главной осью и фокусными расстояниями f ₁ и f ₂ эквивалентное фокусное расстояние F дается формулой

Если обе линзы совместить, т.е. считать, что a  0, то получим

Величина, обратная фокусному расстоянию (с учетом знака), называется оптической силой. Если фокусное расстояние измеряется в метрах, то соответствующая оптическая сила выражается в диоптриях. Как явствует из последней формулы, оптическая сила системы близко расположенных тонких линз равна сумме оптических сил отдельных линз.

Оптическая система - это совокупность отражающих, преломляющих и ограничивающих поверхностей, которые отделяют друг от друга оптически однородные среды. Обычно эти поверхности являются сферическими или плоскими. Если центры всех поверхностей лежат на одной прямой, то оптическая система называется центрированной. Центрированные оптические системы могут включать в себя плоские зеркала и отражающие призмы, ломающие оптическую ось, но, по сути, не влияющие на симметрию системы (рис.17). Чтобы центрированная система была идеальной оптической системой, необходимо ограничиться только лучами, идущими под малыми углами к главной оптической оси. Такие лучи называются параксиальными (нулевые). Теория идеальных оптических систем была развита Гауссом (1841).

Ограничения пучков лучей

Ограничения пучков в оптических системах связаны с конечностью физических размеров оптических элементов. Эти ограничения обозначаются на схемах и чертежах в виде диафрагм, роль которых могут играть оправы линз, а также отдельно стоящие диафрагмы.

Ограничение размера пучков - результат совместного действия всех имеющихся в оптической системе диафрагм. Однако можно выделить одну (наименьшую) диафрагму, и считать, что остальные не ограничивают ход лучей. Такая диафрагма называется апертурной (рис.18.).

Апертура (apertus - открытый) - это понятие, которое в геометрической оптике определяет размер пучка лучей.

Апертурная диафрагма - это диафрагма, которая ограничивает размер осевого пучка (идущего из осевой точки предмета).

Луч, идущий из осевой точки предмета и проходящий через край апертурной диафрагмы называется апертурным лучом.

Рассмотрим апертурную диафрагму и предшествующую ей часть оптической системы.

Параксиальное изображение апертурной диафрагмы в пространстве предметов, сформированное предшествующей частью оптической системы в обратном ходе лучей, называется входным зрачком оптической системы.

Если апертурная диафрагма находится в пространстве предметов, то входным зрачком является сама апертурная диафрагма.

Выходной зрачок - это параксиальное изображение апертурной диафрагмы в пространстве изображений, сформированное последующей частью оптической системы в прямом ходе лучей.

Если апертурная диафрагма находится в пространстве изображений, то выходным зрачком является сама апертурная диафрагма.

Входной зрачок, выходной зрачок и апертурная диафрагма сопряжены. Апертурный луч внутри системы проходит через край апертурной диафрагмы, в пространстве предметов - через край входного зрачка, а в пространстве изображений - через край выходного зрачка.

Главный луч - это луч, идущий из внеосевой точки предмета и проходящий через центр апертурной диафрагмы.

По законам параксиальной оптики главный луч также проходит через центр входного зрачка в пространстве предметов и через центр выходного зрачка в пространстве изображений (рис.19).

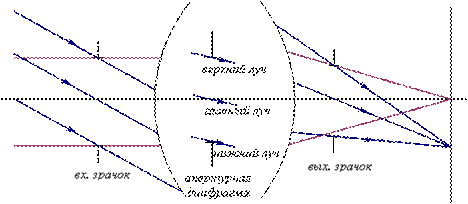Верхний луч внеосевого пучка - это луч, проходящий через верхний край апертурной диафрагмы и соответствующие ему сопряженные точки входного и выходного зрачков.

Рис.19. Внеосевой пучок.

Поле - это часть плоскости предметов, которая изображается оптической системой. В реальной оптической системе поле ограничивается полевой диафрагмой.

Поиск по сайту: