Выделение полного квадрата

.

, далее учесть, что , .

Разложение квадратного трехчлена на множители

.

где - корни квадратного трехчлена

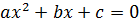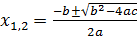, , если коэффициент b-четный, то удобнее использовать следующую формулу:

.

Тригонометрические формулы

ü Функции одного угла

; ; , ; ; .

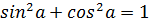ü Функции кратных углов

; ; .

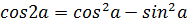ü Функции половинного угла

; .

ü Произведение функций

;

;

.

ü Универсальная тригонометрическая подстановка

; .

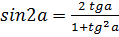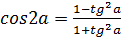Гиперболические функции

; ; .

Основные формулы гиперболической тригонометрии

; ; .

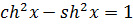Таблица производных элементарных функций

Функция	Производная
С (постоянная)
x

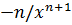
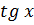
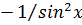
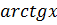
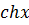
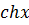
Правила дифференцирования

; ; ; .

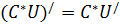Производная сложной функции (функции от функции - цепное правило)

; ; ;

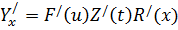
В случае длинной цепочки поступают аналогично.

Свойства дифференциала

, , , где С-константа.

Общие правила интегрирования

Постоянный множитель можно выносить за знак интеграла:

.

Интеграл суммы (разности) равен сумме (разности) интегралов от слагаемых:

, где u,v,w – функции от x.

Правило подстановки:

если x=z(t), то .

Интегрирование по частям

, где u,v – функции от x.

В дальнейшем во всех формулах постоянная интегрирования опущена, первообразные, содержащие , следует понимать как , знак абсолютной величины опущен для простоты.

Таблица основных интегралов

Степенные функции	Показательные функции
; .	.
.	.
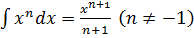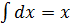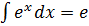Тригонометрические функции	Гиперболические функции
.	.
.	.
.	.
.	.
.	.
.	.
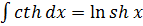Дробно-рациональные функции	Иррациональные функции
.	.
.	.
.	.

Интегрирование иррациональных функций

Эти интегралы вычисляются с помощью следующих подстановок:

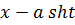; или
;

; ;

;

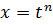
(n-наименьшее общее кратное показателей всех радикалов, под которым X входит в подынтегральную функцию)

, Интегралы этого вида после выделения полного квадрата под корнем линейными подстановками сводятся к следующим:

1) если а > 0, то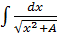

2) если а < 0, то

Поиск по сайту: