Механічні коливання

Механічні коливання і хвилі. Біоакустика

Механічні коливання, що відбуваються під дією сили, пропорційної зміщенню і напрямленої до положення рівноваги, називаються гармонічними коливаннями і описуються гармонічним законом:

(2.13)

Тут – зміщення тіла (точки) від положення рівноваги, – амплітуда, - циклічна частота, – період, - початкова фаза.

Швидкість коливань тіла (точки):

(2.14)

З рівняння (2.14) випливає, що швидкість коливання змінюється з часом. Отже, коливальний рух відбувається з прискоренням:

(2.15)

Рис. 2.13

Для наочності, зміна , і з часом (при гармонічному коливанні), розраховані по формулах (2.13-2.15) при представлені на рис. 2.12.

Коли на тіло діє лише сила пружності:

(2.16)

тут 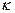– коефіцієнт жорсткості, тоді згідно з другим законом Ньютона, враховуючи (2.15) одержимо:

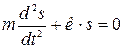
(2.17)

Позначивши через 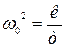, отримуємо диференціальне рівняння гармонічного коливання:

(2.18)

Розв’язком цього рівняння є функція – задана формулою (2.13).

Оскільки всередині коливальної системи завжди присутня сила тертя, то гармонічні коливання будуть затухати і з часом зовсім зникнуть. При невеликих швидкостях руху можна вважати, що сила тертя пропорційна швидкості руху тіла:

(2.19)

де 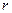– коефіцієнт опору середовища. Тоді другий закон Ньютона, для розглядуваного випадку, запишимо у вигляді:

(2.20)

Позначивши ( - коефіцієнт затухання), отримаємо диференціальне рівняння затухаючих коливань:

(2.21)

розв’язком якого є функція (рис. 2.14):

(2.22)

Рис.2.14

де .

Залежність зміни амплітуди з часом має вигляд:

(2.23)

і графічно показана на рис. 2.14.

Період затухаючих коливань визначається за формулою:

(2.24)

Відношення двох сусідніх амплітуд, розділених інтервалом часу, рівним періоду коливань, називається декрементом затухання і позначається буквою дельта :

(2.25)

У практиці частіше використовують логарифмічний декремент , який за визначенням:

(2.26)

Коливанням, які виникають в системі при дії зовнішньої сили, що змінюється за періодичним законом, називаються вимушеними коливаннями.

Якщо на матеріальну точку крім квазіпружної сили і сили тертя діє зовнішня вимушуюча сила

,

(2.27)

де F₀ – її амплітуда, - кругова частота вимушуючої сили, то другий закон Ньютона матиме вигляд:

,

(2.28)

або

(2.29)

де .

Розв’язок цього рівняння має вигляд:

(2.30)

де

,

(2.31)

Резонансна кругова частота, при якій зміщення досягає максимальної амплітуди визначається за формулою:

(2.32)

Амплітуда при резонансі дорівнює:

(2.33)

Залежність амплітуди коливань від частоти представлена на рис.2.15 ().

Рис. 2.15

При дії зовнішніх механічних коливань, резонансні коливання відбуваються і у внутрішніх органах. У цьому, очевидно, одна з причин негативного впливу інфразвукових коливань і вібрацій на організм людини.

Існують коливальні системи, у яких підтримуються незатухаючі коливання власної частоти. Такі системи називаються автоколивальними, а коливання, що в них відбуваються – автоколиваннями.

Поиск по сайту: