В чому полягає мета перевірки гіпотези про закон розподілу ряду?

Однією з найважливіших задач математичної статистики є встановлення теоретичного закону розподілу випадкової величини, що характеризує ознаку, що вивчається за дослідним (емпіричним) розподілом, що являє собою статистичний ряд.

Для розв’язання такої задачі необхідно визначити вид та параметри закону розподілу.

Пропозиція щодо закону розподілу може бути висунута з теоретичних посилань, досвіду аналогічних випробувань або графічного зображення емпіричного закону розподілу.

Параметри розподілу, як правило, невідомі, тому їх заміняють найкращими оцінками за вибіркою.

Між теоретичним та емпіричними законами завжди існуватимуть розбіжності (як би добре не був би підібраний закон). Виникає відповідно питання – чи можна пояснити ці розбіжності лише впливом деяких випадкових обставин (пов’язаних з обмеженою кількістю спостережень) чи вона є істотними та пов’язані з тим, що теоретичний закон підібрано погано. Для відповіді на це питання і використовують критерії згоди.

Хай необхідно перевірити нульову гіпотезу Н₀ про те, що дослідна величина Х розподілена за певним законом розподілу. Для перевірки гіпотези Н₀ обирають деяку випадкову величину U, що характеризує ступінь розходження теоретичного та емпіричного розподілів, закон розподілу якої при достатньо великих n відомий та практично не залежить від закону розподілу випадкової величини Х.

Якщо відомий закон розподілу U, то можна знайти ймовірність того, що U прийняла значення не менше ніж, фактично спостерігаєме у досліді u, тобто U≥u. Якщо P(U≥u)=α мала, то це позначає у відповідності до принципу практичної впевненості, що такі, як у досліді, та більші відхилення практично неможливі. В цьому випадку нульову гіпотезу відкидають. Якщо ж ймовірність P(U≥u)=α не мала, то гіпотезі Н₀ можна вважати такою, що не містить протиріч до вибіркових даних.

Χ² – критерій Пірсона. На практиці частіше за всього використовують Χ² – критерій Пірсона у ньому у якості міри розходження U береться величина Χ², що дорівнює сумі квадратів відхилень частостей (статистичних ймовірностей) w_i від гіпотетичних р_і, що розраховані за розподілом, що передбачається, та взяті з деякими вагами с_і.

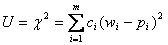
Ваги с_і вводяться таким чином, щоб при одних і таких самих відхиленнях 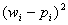більшу вагу мали відхилення, при яких р_і мала та меншу вагу – при яких р_і велика. Очевидно, так можна зробити, якщо взяти с_і обернено пропорційними ймовірностям p_i. Взяв у якості ваг 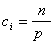, можна довести, що при n->∞ статистика

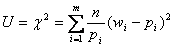
або

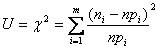
має Χ² – розподіл з k=m–r-1 степенями вільності, де m – кількість інтервалів емпіричного розподілу (статистичного ряду); r – кількість параметрів теоретичного розподілу, що обчислені за дослідними даними.

nw_i та np_i – відповідно емпіричні та теоретичні частоти.

Схему застосування критерію Χ² можна звести до наступного:

1. Визначається міра розходження емпіричних та теоретичних частот Χ².
2. Для обраного рівня значущості α за таблицею Χ²-розподілу знаходять критичне значення Χ²_α;k при кількості ступенів волі k=m–r–1.
3. Якщо значення Χ², що фактично спостерігається більше критичного, тобто Χ²>Χ²_α;k, то гіпотеза Н₀ відкидається, якщо Χ²≤Χ²_α;k, то гіпотеза не містить протиріч до вибіркових даних.

Зауваження. Статистика

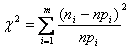
має Χ² розподіл лише при n->∞, тому необхідно, щоб у кожному інтервалі була достатня кількість спостережень (хоча б 5). Якщо в якому-небудь інтервалі кількість спостережень менша за 5, має сенс об’єднати сусідні інтервали, щоб в об’єднаних інтервалах частота була не менша з 5.

Поиск по сайту: