 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Средствами десятичной арифметики
То есть:
1. Дано число в системе счисления «q». Например, дано двоичное число (или восьмеричное число, или шестнадцатиричное число).
2. Надо пронумеровать цифры от запятой справа налево (начинаем нумерацию числом «0», затем «1», «2» и так далее), от запятой слева направо (начинаем нумерацию числом «–1», затем «–2», «–3» и так далее). Примечание: если число целое, то нумеровать надо справа налево (начинаем нумерацию числом «0», затем «1», «2» и так далее).
3. Разложить на многочлен сокращенную запись выражения.
4. Решить полученный многочлен.
5. Приписать к полученному числу основание 10.
Пример 1.
Переведите число 1011,12 в десятичную систему счисления.
Решение:
| Число | 1 0 1 1, 1 2 = 1 * 2 3 + 0 * 2 2 + 1 * 2 1 + 1 * 2 0 + 1 * 2 –1 = 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1 + 1 * 0,5 = |
| Разряды | 3 2 1 0 -1 |
| = 8 + 0 + 2 + 1 + 0,5 = 11,5 10 |
Дробные числа можно записывать и обыкновенной дробью. Тогда решение будет выглядеть следующим образом:
| Число | 1 0 1 1, 1 2 = 1 * 2 3 + 0 * 2 2 + 1 * 2 1 + 1 * 2 0 + 1 * 2 –1 = 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1 + 1 * 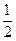 = =
|
| Разряды | 3 2 1 0 -1 |
= 8 + 0 + 2 + 1 + 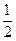 = = 
|
Пример 2.
Переведите число 276,528 в десятичную систему счисления.
Решение:
| Число | 2 7 6, 5 2 8 = 2 * 8 2 + 7 * 8 1 + 6 * 8 0 + 5 * 8 -1 + 2 * 8 –2 = |
| Разряды | 2 1 0 -1 -2 |
| = 2 * 64 + 7 * 8 + 6 * 1 + 5 * 0,125 + 2 * 0,015625 = = 128 + 56 + 6 + 0,625 + 0,03125 = = 190,65625 10 |
или:
| Число | 2 7 6, 5 2 8 = 2 * 8 2 + 7 * 8 1 + 6 * 8 0 + 5 * 8 -1 + 2 * 8 –2 = |
| Разряды | 2 1 0 -1 -2 |
= 2 * 64 + 7 * 8 + 6 * 1 + 5 * 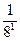 + 2 * + 2 * 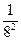 =
= 128 + 56 + 6 + 5 * =
= 128 + 56 + 6 + 5 * 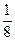 + 2 * + 2 * 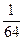 =
= 190 + =
= 190 + 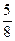 + + 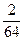 = 190 + = 190 + 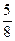 + + 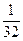 = 190 + = 190 + 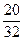 + + 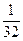 = 190 + = 190 + 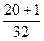 =
= 190 + =
= 190 + 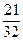 = = 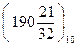
|
Примечание:
1. Дроби НАДО сократить!
2. Дроби НЕЛЬЗЯ округлять!
Пример 3.
Переведите число А32,С16 в десятичную систему счисления.
Решение:
| Число | А 3 2, С 16 = А * 16 2 + 3 * 16 1 + 2 * 16 0 + С * 16 –1 = А * 256 + 3 * 16 + 2 * 1 + С * 0,0625 = |
| Разряды | 2 1 0 -1 |
| = 10 * 256 + 3 * 16 + 2 * 1 + 12 * 0,0625 = = 2560 + 48 + 2 + 0,75 = 2610,75 10 |
или:
| Число | А 3 2, С 16 = А * 16 2 + 3 * 16 1 + 2 * 16 0 + С * 16 –1 = А * 256 + 3 * 16 + 2 * 1 + С * 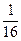 = =
|
| Разряды | 2 1 0 -1 |
= 10 * 256 + 3 * 16 + 2 * 1 + 12 * 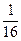 =
= 2560 + 48 + 2 + =
= 2560 + 48 + 2 + 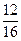 = 2610 + = 2610 + 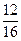 = 2610 + = 2610 + 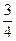 = = 
|
Примечание:
1. Дроби НАДО сократить!
2. Дроби НЕЛЬЗЯ округлять!
Примеры задач на основе «перевода из одной системы счисления в другую»
Задача 1:
Какое наибольшее десятичное число можно записать четырьмя цифрами:
1) в двоичной системе;
2) в пятеричной системе;
3) в девятеричной системе;
4) в шестнадцатеричной системе?
Решение:
11112 = 1 * 23 + 1 * 22 + 1 * 21 + 1 * 20 = 8 + 4 + 2 + 1 = 1510
44445 = 4 * 53 + 4 * 52 + 4 * 51 + 4 * 50 = 4 * 125 + 4 * 25 + 4 * 5 + 4 * 1 = 500 + 100 + 20 + 4 = 62410
88889 = 8 * 93 + 8 * 92 + 8 * 91 + 8 * 90 = 8 * 729 + 8 * 81 + 8 * 9 + 8 * 1 = 5832 + 648 + 72 + 8 = 656010
FFFF16 = F * 163 + F * 162 + F * 161 + F * 160 = 15 * 163 + 15 * 162 + 15 * 161 + 15 * 160 =
= 15 * 4096 + 15 * 256 + 15 * 16 + 15 * 1 = 61440 + 3840 + 240 + 15 = 6553510
Задача 2.
В какой системе счисления справедливо следующее: 21 + 24 = 100?
Решение.
Пусть x – искомое основание системы счисления. То есть 21х + 24х = 100х
Тогда
100x = 1 · x2 + 0 · x1 + 0 · x0 = x2
21x = 2 · x1 + 1 · x0 = 2x + 1,
24x = 2 · x1 + 4 · x0 = 2х + 4.
Таким образом, вместо 21х + 24х = 100х запишем (2x + 1) + (2х + 4) = x2
Решим полученное уравнение.
x2 – 4x – 5 = 0.
х1 = – 1, х2 = 5
Проверим, подходят ли корни.
х1 = – 1 – не подходит, так отрицательное число
х2 = 5 – подходит, так как: во-первых, положительное число;
во-вторых, нет противоречия: 215 – верно (2<5, 1<5)
245 – верно (2<5, 4<5)
1005 – верно (1<5, 0<5)
Ответ. Выражение верно в пятеричной системе счисления.
Примечание: при проверке корней надо учитывать, что:
· Самой маленькой позиционной системой счисления является двоичная система счисления (в рассмотрении современной компьютерной техники).
· Система счисления – натуральное число. То есть система счисления НЕ может быть отрицательным числом и НЕ может быть дробью.
· Цифры, из которых состоят числа (данные в примере), должны быть СТРОГО МЕНЬШЕ полученного корня (по определению основания системы счисления).
· Если ни один из корней уравнения не подходит, ответом будет фраза «нет решений».
Задача 3.
В какой системе счисления справедливо следующее: 37 + 18 + 11 = 102?
Решение.
Пусть x – искомое основание системы счисления. То есть 37х + 18х + 11х = 102х
Тогда
102x = 1 · x2 + 0 · x1 + 2 · x0 = x2 + 2
37x = 3 · x1 + 7 · x0 = 3x + 7,
18x = 1 · x1 + 8 · x0 = х + 8,
11x = 1 · x1 + 1 · x0 = х + 1.
Таким образом, вместо 37х + 18х + 11х = 102х запишем (3x + 7) + (х + 8) + (x + 1) = x2 + 2
Решим полученное уравнение.
3x + 7 + х + 8 + x + 1 = x2 + 2
5x + 16 = x2 + 2
x2 + 2 – 5x – 16 = 0
x2 – 5x – 14 = 0.
х1 = – 2, х2 = 7
Проверим, подходят ли корни.
х1 = – 2 – не подходит, так отрицательное число
х2 = 7 – не подходит, так как:
С одной стороны, это положительное число. Это правильно.
НО, с другой стороны, проверим соответствие «цифр в данных числах» и «найденого корня».
377 – не верно (3<7, но 7=7, такого быть не может)
187 – не верно (1<7, но 8>7, такого быть не может)
117 – верно (1<5, 1<5)
1027 – верно (1<5, 0<5, 2<5)
Ответ. Нет решений.
Поиск по сайту: