 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Позиционная система счисления
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы.
Сама же запись числа 757,7 означает сокращенную запись выражения
700 + 50 + 7 + 0,7 = 7 * 102 + 5 * 101 + 7 * 100 + 7 * 10-1 = 757,7.
Любая позиционная система счисления характеризуется своим основанием.
Основание позиционной системы счисления – количество различных цифр, используемых для изображения чисел в данной системе счисления.
За основание системы можно принять любое натуральное число – два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел (an-1 ... a0 , a-1 a-2... a-m)q в каждой из систем счисления с основанием q означает сокращенную запись выражения
an-1 * qn-1 + an-2 * qn-2 +... + a1 * q1 + a0 * q0 + a-1 * q-1 +... + a-m * q-m,
где ai – цифры системы счисления (цифры данного числа)
n – число целых разрядов (количество цифр до запятой)
m – число дробных разрядов (количество цифр после запятой)
(an-1 ... a0 , a-1 a-2... a-m)q – число, записанное в системе счисления q
Пример 1:
| Число | 1 0 1 1, 1 2 = 1 * 2 3 + 0 * 2 2 + 1 * 2 1 + 1 * 2 0 + 1 * 2 –1 |
| Разряды | 3 2 1 0 -1 |
В этом примере: (an-1 ... a0 , a-1 a-2... a-m)q = (1 0 1 1, 1) 2
q = 2
n = 4 (то есть n – 1 = 3)
m = 1
an - 1 = a4 - 1 = a3 = 1
an - 2 = a4 - 2 = a2 = 0
an - 3 = a4 - 3 = a1 = 1
an - 4 = a4 - 4 = a0 = 1
a - m = a - 1= 1
Примечание.
Нумеруем цифры
1. От запятой справа налево по целой части. Нумерация начинается с «нуля». Далее «единица», далее «два», далее «три» и так далее.
2. От запятой слева направо по дробной части. Нумерация начинается с «минус единицы». Далее «минус два», далее «минус три», далее «минус четыре» и так далее.
Пример 2:
| Число | 2 7 6, 5 2 8 = 2 * 8 2 + 7 * 8 1 + 6 * 8 0 + 5 * 8 -1 + 2 * 8 –2 |
| Разряды | 2 1 0 -1 -2 |
Кроме десятичной широко используются системы с основанием, являющимся целой степенью числа 2, а именно:
· двоичная (используются цифры 0, 1);
· восьмеричная (используются цифры 0, 1,..., 7);
· шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1,..., 9, а для следующих чисел – от десяти до пятнадцати – в качестве цифр используются символы A, B, C, D, E, F). Примечание: А = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
В компьютерной (вычислительной) технике используется двоичная система счисления в качестве основной. Эта система счисления является минимальной позиционной системой счисления.
Полезно запомнить запись в этих системах счисления первых двух десятков целых чисел:
| ()10 | ()2 | ()8 | ()16 |
| A |
| ()10 | ()2 | ()8 | ()16 |
| B | |||
| C | |||
| D | |||
| E | |||
| F | |||
Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления.
Перевод из одной системы счисления в другую
Правило 1.
Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.
То есть:
1. Точка отсчета в таком делении – запятая. От неё «движемся» влево по целой части числа и вправо по дробной части числа. Примечание: если число целое, то движемся справа налево.
2. Делим (дугами) на группы по три цифры (для перевода в восьмеричную систему счисления) или на группы по четыре цифры (для перевода в шестнадцатиричную систему счисления).
3. Если цифр для «группы» не хвататает, то приписываем нули (справа для дробной части, слева для целой части). Приписываение нулей не нарушает правила математики: если к целой части приписать слева нули (если к дробной части присать справа нули), то число не изменится. Примечание: если нули не приписать, то будет ошибка на следующем этапе решения!
4. Каждую группу цифр заменяем на одну цифру (например, по таблицам).
5. Записать ответ, не забыв написать запятую и основание системы счисления
| ()2 | ()8 |
| ()2 | ()16 |
| A | |
| B | |
| C | |
| D | |
| E | |
| F |
Пример 1.
Переведите число из двоичной системы в восьмеричную: 1110101,101112
Решение:
1. Движемся от запятой влево по целой части и вправо по дробной части.

2. Разделим число на группы по три цифты (делим число на триады), начиная о запятой (то есть «двигаемся» от запятой влево по целой части и вправо по дробной части).
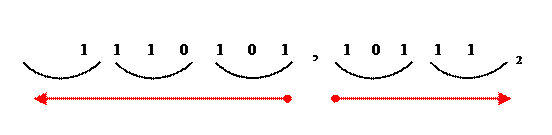
3. Припишем нули, если не хватает цифр для полной группы (состоящей из трех цифр)
В данном случае надо приписать два нуля в целой части, то есть приписать два нуля слева. И надо приписать один нуль в дробной части, то есть приписать один нуль справа.

4. Используя таблицу, заменим каждую такую группу (смотрим на двоичный столбик) одной цифрой (смотрим на соответствующий восьмеричный столбик)
| ()2 | ()8 |

5. Запишем ответ, не забыв написать запятую и основание системы счисления.
Ответ: 165,568
Запись примера (в тетради):

Пример 2.
Переведите число из двоичной системы в шестнадцатиричную: 1110101,101112
Решение:
1. Движемся от запятой влево по целой части и вправо по дробной части.

2. Разделим число на группы по четыре цифты (делим число на тетрады), начиная о запятой (то есть «двигаемся» от запятой влево по целой части и вправо по дробной части).

3. Припишем нули, если не хватает цифр для полной группы (состоящей из четырех цифр)
В данном случае надо приписать один нуль в целой части, то есть приписать один нуль слева. И надо приписать три нуля в дробной части, то есть приписать три нуля справа.

4. Используя таблицу, заменим каждую такую группу (смотрим на двоичный столбик) одной цифрой (смотрим на соответствующий шестнадцатиричный столбик)
| ()2 | ()16 |
| A | |
| B | |
| C | |
| D | |
| E | |
| F |

5. Запишем ответ, не забыв написать запятую и основание системы счисления.
Ответ: 75,В816
Запись примера (в тетради):

Правило 2.
Для перевода целого десятичного числа N в систему счисления с основанием q необходимо N разделить с остатком ("нацело") на q, записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q, и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа N в новой системе счисления будет последовательность остатков деления, изображенных одной q -ичной цифрой и записанных в порядке, обратном порядку их получения.
То есть:
1. Дано целое десятичное число. Его надо перевести в любую другую систему счисления. Например, перевести данное число в двоичную систему счисления, в восьмеричную систему счисления, в шестнадцатиричную систему счисления.
2. Сначала разделим число с остатком на новое основание (например, раздели на 2, если надо перевести в двоичную систему счисления).
3. Затем полученное неполное частное (если оно не равно нулю) снова разделим на это основание.
4. Так делим до тех пор, пока неполное частное не станет равным нулю.
5. Далее записываем полученные остатки в порядке, обратном их получения. То есть смотрим остатки справа налево. Примечание: для шестнадцатиричной системы счисления надо не забыть, что часть цифр записывается буквами.
6. В ответе надо приписать основание системы счисления, в которую переводили данное число.
Пример 1.
Переведите число 75 из десятичной системы в двоичную.
Решение:
1. Разделим нацело: данное число 75 на 2 (так как надо перевести в двоичную систему счисления).
Число 2 помещается в числе 75: 37 раз. При этом остается остаток равный 1.

2. Полученное неполное частное 37 не равно нулю. Поэтому разделим его нацело на 2.
Число 2 помещается в числе 37: 18 раз. При этом остается остаток равный 1.

3. Полученное неполное частное 18 не равно нулю. Поэтому разделим его нацело на 2.
Число 2 помещается в числе 18: 9 раз. При этом остается остаток равный 0.

4. Аналогично выполняем деление до тех пор, пока неполное частное не станет равным нулю. В итоге получим следующую запись:

5. Запишем остатки в обратном порядке
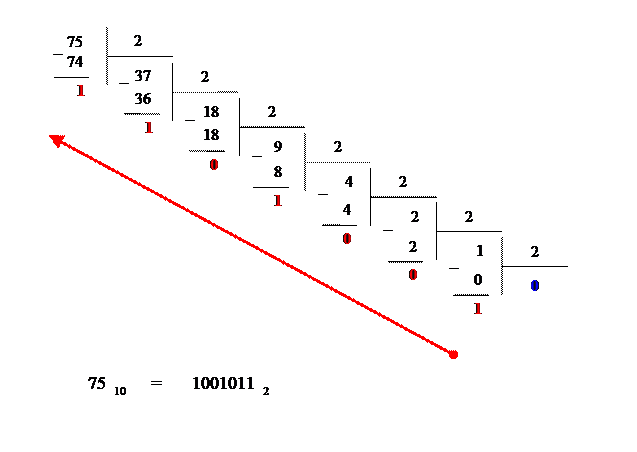
Пример 2.
Переведите число 75 из десятичной системы в восьмеричную.
Решение:
Аналогично примеру 1.

Пример 3.
Переведите число 75 из десятичной системы в шестнадцатиричную.
Решение:
Аналогично примеру 1. НО надо ВНИМАТЕЛЬНО записывать остатки, не забыв про буквы!

Правило 3.
Перевод в десятичную систему числа x, записанного в q -ичной системе счисления (например, q = 2, 8 или 16) в виде xq = (an-1 ... a0 , a-1 a-2... a-m)q сводится к вычислению значения многочлена
x q = an-1 * qn-1 +... + a0 * q0 + a-1 * q -1 + a-2 * q-2 +... + a-m * q-m
Поиск по сайту: