 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Корреляционно-регрессионный анализ
Выборочных показателей группы студентов
Определить форму и направление взаимосвязи между показателями а) 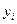 и
и  , б)
, б) 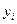 и
и  у 19 исследуемых с помощью корреляционного поля.
у 19 исследуемых с помощью корреляционного поля.
а) 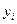 - средний балл успеваемости студента группы 811 за первый семестр 2008-2009 учебного года;
- средний балл успеваемости студента группы 811 за первый семестр 2008-2009 учебного года;  - количество учебных дней пропущенных студентом за семестр.
- количество учебных дней пропущенных студентом за семестр.
б) 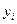 - средний балл успеваемости студента группы 811 за первый семестр 2008-2009 учебного года;
- средний балл успеваемости студента группы 811 за первый семестр 2008-2009 учебного года;  - количество часов в день в среднем, потраченное на выполнение домашнего задания студентом за 1семестр.
- количество часов в день в среднем, потраченное на выполнение домашнего задания студентом за 1семестр.
 Корреляционные поля
Корреляционные поля
а)
 б)
б)
Расчет нормированного коэффициента корреляции Пирсона производим по формуле:  , с учётом того, что мы предположили о наличии линейной зависимости.
, с учётом того, что мы предположили о наличии линейной зависимости.
а)  -0,54
-0,54
Рассчитаем число степеней свободы:
К = n –2, K = 19 – 2 = 17
б)  ,
,
Рассчитаем число степеней свободы:
К = n –2, K = 19 – 2 = 17
Рассчитаем уравнение прямолинейной регрессии для показателей а) 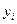 и
и  , б)
, б) 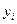 и
и 
а) 


 Т.е.
Т.е.  ,
,  (*)
(*)
Рассчитаем абсолютные погрешности уравнений регрессии по формулам:




Рассчитаем относительные погрешности уравнений регрессии по формулам
 ,
, 
 %,
%,  %
%
С целью расширения возможностей анализа, используется частный коэффициент эластичности, определяемый по формуле: 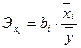 , где
, где  - среднее значение соответствующего факторного признака;
- среднее значение соответствующего факторного признака;  - среднее значение результативного признака; bi- коэффициент регрессии при соответствующем факторном признаке. Коэффициент эластичности показывает, на сколько в среднем изменится значение результативного признака при изменение факторного признака на 1%.
- среднее значение результативного признака; bi- коэффициент регрессии при соответствующем факторном признаке. Коэффициент эластичности показывает, на сколько в среднем изменится значение результативного признака при изменение факторного признака на 1%.
Высчитаем его для нашего случая  =-0,08
=-0,08
б) 
Рассчитаем конечный вид уравнений прямолинейной регрессии:


Т.е.  ,
, 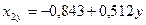
Рассчитаем абсолютные погрешности уравнений регрессии по формулам:


Рассчитать относительные погрешности уравнений регрессии по формулам
 %,
%,  %
%
Высчитаем коэффициент эластичности для данного факторного показателя  =0,169.
=0,169.
Поиск по сайту: