Решение систем нелинейных уравнений методом простой итерации

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ

1. Решение систем нелинейных уравнений методом простой итерации.

2. Алгоритм метода простой итерации при решении систем нелинейных уравнений.

Листинг примера 1

4. Программная реализация решения систем нелинейных уравнений методом простой итерации в MathCad.

Заключение.

Список использованных источников.

ВВЕДЕНИЕ

Решение систем нелинейных уравнений является в общем случае задачей несравненно более сложной, нежели решение систем линейных уравнений. Не существует методов, которые гарантировали бы успех решения любой такой задачи.

Как и для отдельных уравнений, наибольшую проблему представляет задача отделения решений (корней). Для системы уравнений с п неизвестными необходимо, во-первых, понять, сколько у нее решений, а во-вторых, выделить области n-мерного пространства, в каждой из которых есть одно и только одно решение, лишь после этого можно говорить о нахождении решений с заданной точностью (оцениваемой в соответствии с используемой метрикой).

Для отделения корней общих методов, гарантирующих успех, не существует. Для системы с двумя неизвестными можно пытаться использовать геометрические построения. В реальных задачах, являющихся этапами моделирования, исследователь обычно догадывается, где примерно находятся корни системы (или по крайней мере тот корень, который его интересует из содержательных условий модели). Описанные ниже приемы, явно или неявно, исходят из того, что задача отделения корней решена и имеется достаточно малая часть n-мерного пространства, в которой находится корень, надлежащийуточнению. Отметим, что уточнение корней ведется почти исключительно итерационными методами.

Часто для решения линейных и нелинейных задач алгебры используют приближенные методы, позволяющие найти корни системы с заданной точностью. Эти методы представляют собой сходящийся итерационный процесс. Они не дают точного решения задачи, однако отличаются несколько большим быстродействием и порой из-за ошибок округления даже при использовании чисел с двойной точностью могут дать ответ точнее, нежели полученный прямыми методами[1].

Решение систем нелинейных уравнений методом простой итерации

Система нелинейных уравнений с неизвестными обычно имеет вид

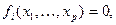
где хотя бы одна функция 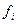нелинейная.

Для решения такой системы в редких случаях можно применить метод последовательного исключения неизвестных, который приводит решение системы к решению одного нелинейного уравнения с одним неизвестным с последующей подстановкой.

Метод простой итерации применим к системам, которые предварительно приведены к виду

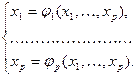
(1.1)

или, в векторной форме,

(1.2)

Пусть 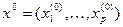— начальное приближение. Последующие приближения в методе простой итерации находятся по формулам

(1.3)

или, в векторной форме,

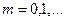
(1.4)

Если последовательность векторов сходится к вектору , а функции непрерывны, то вектор 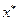является решением системы (1.2). Для получения условий сходимости метода итераций введем в -мерном векторном пространстве какую-либо норму (например, кубическую, октаэдрическую или сферическую).

Теорема. Пусть для уравнения (1.2) и начального приближения выполнены условия:

1) для из сферы

(1.5)

вектор-функция удовлетворяет условию

(1.6)

где ;

2)

Тогда уравнение (1.2) в сфере (1.5) имеет единственное решение 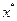, к нему сходится последовательность (1.4) и погрешность метода оценивается неравенством

(1.7)

Сходимость метода итераций считается хорошей, если .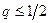

Приведем достаточное условие, обеспечивающее выполнение неравенства (1.6) в кубической норме. Сфера (1.5) в кубической норме является -мерным кубом с центром в точке :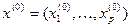

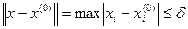
(1.8)

Предположим, что в кубе (1.8) функции 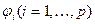имеют непрерывные частные производные Неравенство (1.6) будет выполнено, если 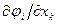удовлетворяют в кубе (1.8)[2].

(1.9)

Пример 1.

Методом простой итерации решить систему

на отрезке с точностью

Решение:

Выделим и 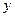в этой системе:

Разделим на 5 и получим:

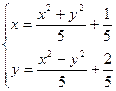
Запишем заданную систему в следующем виде:

Проверим сходимость итерационного процесса:

;

.

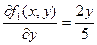Отсюда

так как

Требование сходимости итерационного процесса выполняется.

В качестве начальных значений выберем . Найдем:

Подставим эти значения и получим:

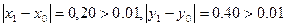
Далее:

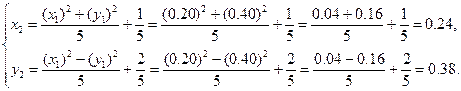
Далее:

Так как , имеем окончательное решение x=0.24, y=0.38.

2.Алгоритм метода простой итерации при решении систем нелинейных уравнений

3. Листинг программы примера

Uses crt;

Var x,y,xn,yn,d,e,f,g,h,i:real;

BEGIN

Writeln('Решим систему уравнений методом простой итерации.');

Readln;

Writeln('Введите начальное значение х');

Readln(x);

Writeln(''Введите начальное значение y');

Readln(y);

Writeln('Введите точность определения корня');

Readln(e);

xn:=x; yn:=y;

d:=(2*x)/5; f:=(2*y)/5;

g:=(2*x)/5; h:=(-2*y)/5;

If (d+f+g+h)<1 then

writeln('Требование сходимости итерационного процесса выполняется')

else writeln('Требование сходимости итерационного процесса не выполняется ');

Readln;

Repeat

BEGIN

x:=xn; y:=yn;

xn:=(x*x+y*y)/5+0.200; yn:=(x*x-y*y)/5+0.400;

i:=i+1;

END;

until (ABS(xn-x)<=e) and (ABS(yn-y)<=e);

if (d+f+g+h)<1 then writeln(' Мы получили ответ x=',xn:0:2,' y=',yn:0:2,

' на ',i:0:0,'шаге итерации.') else Writeln('Нет решений');

Readln;

END.

Поиск по сайту: