Циклические коды CRC

Циклический избыточный контроль CRC (Cyclic redundancy check) - это метод обнаружения ошибок с использованием полиномиального кода. Полиномы представляют собой альтернативную запись чисел в двоичной системе. Например, двоичному числу 1100 соответствует полином .

Для полиномов определяются операции сложения, вычитания, умножения и деления, которые используются для кодирования и декодирования сообщения. Особенностью всех арифметических операций над полиномами является отсутствие переносов и заемов.

Правила полиномиального арифметического сложения без переноса:

0 + 0 = 0; 0 + 1 = 1; 1 + 0 = 1; 1 + 1 = 0.

Правила полиномиального арифметического вычитания без переноса:

0 - 0 = 0; 0 - 1 = 1; 1 - 0 = 1; 1 - 1 = 0.

Полиномиальные арифметическое сложение и вычитания соответствуют логической операции сумма по модулю два: 0 Å 0=0; 0 Å 1=1; 1 Å 0=1; 1 Å 1=0.

Правила полиномиального арифметического умножения выполняются по обычным правилам арифметического умножения:

0 0 = 0; 0 1 = 0; 1 0 = 0; 1 1 = 1.

Сложение промежуточных результатов умножения выполняется по правилам полиномиального арифметического сложения без переноса (сумма по модулю два).

При умножении полиномов степени складываются:

Правила полиномиального арифметического деления выполняются по обычным правилам арифметического деления. Вычитание промежуточных результатов деления выполняется по правилам полиномиального арифметического вычитания без переноса (сумма по модулю два).

Алгоритм вычисления CRC основан на свойствах деления с остатком двоичных полиномов (многочленов).

Циклические коды задаются с помощью порождающих полиномов:

,

где 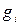= {0,1}; x = 2.

Полином исходного сообщения имеет вид:

.

Полином кодированного сообщения имеет вид:

.

Пример. Переход от двоичного представления числа к полиномиальному выполняется следующим образом. Пусть дано восьмиразрядное двоичное число 01010011. В таблице приведены соответствия между номерами, значениями битов и переменными полинома.

Таблица Соответствие между двоичными числами и полиномом

Номер бита
Значение бита
Переменная полинома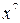

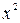
Двоичное число 01010011 переводится в полиномиальную форму следующим образом:

01010011 = 0∙ 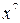+ 1∙ + 0∙ + 1∙ + 0∙ + 0∙ + 1∙ + 1∙ =

= 0 + + 0 + + 0 + 0 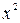+ + = + + + = + + + 1.

Получаем 01010011 = + + + 1.

Порядок кодирования и декодирования данных методом CRC.

Кодирование данных и передача по линии связи:

1. Выбор исходного полинома:

.

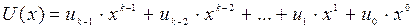2. Умножение исходного полинома на фиксированное двоичное число :

.

3. Деление 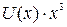на порождающий полином

:

.

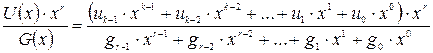Результатом является:

- - полином (частное от деления);

- - полином (остаток) с максимальной степенью (r - 1).

4. Кодированное сообщение представляется в виде:

=

= .

5. Передача сообщения .

Прием и проверка данных:

1. Прием сообщения .

2. Деление сообщения на порождающий полином :

.

Результатом является - полином (частное от деления); - полином (остаток) с максимальной степенью (r - 1).

3. Проверка на наличие ошибок:

- если остаток равен нулю, то ошибки нет;

- если остаток равен не нулю, то ошибка есть.

Пример. Передать исходный полином с CRC - кодированием циклического кода (7,4,3).

Кодирование данных и передача по линии связи: Рассмотрим последовательность кодирования:

- исходный полином = ;

- порождающий полином = ;

- множитель .

1. Умножение исходного полинома на фиксированное двоичное число :

.

2. Деление полинома на порождающий полином и вычисление остатка :

							=
					=

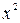
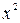
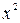
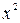
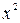
Получаем остаток , равный х.

4. Формирование сообщения:

= .

5. Передача сообщения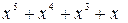

Прием и проверка данных:

1. Прием сообщения .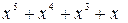

2. Деление сообщения на порождающий полином :

							=
					=

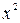
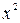
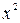
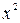
3. Проверка на наличие ошибок:

- остаток равен нулю, ошибки нет.

Пример. Передать исходный полином с CRC - кодированием циклического кода (7,4,3) в двоичных кодах.

Кодирование данных и передача по линии связи: Рассмотрим последовательность кодирования:

- исходный полином = = 0111;

- порождающий полином = = 1011;

- множитель = 1000.

1. Умножение исходного полинома = 111 на фиксированное двоичное число = 1000:

= (0111)∙ 1000 = 0111000.

2. Деление полинома = 111000 на порождающий полином = 1011:

							=

Остаток = 10.

3. Формирование сообщения:

= .

4. Передача сообщения 0111 010.

Прием и проверка данных:

1. Прием сообщения 0111 010.

2. Деление сообщения = 0111 010 на порождающий полином

= 1011:

							=

3. Проверка на наличие ошибок:

- остаток равен нулю, ошибки нет.

Поиск по сайту: