 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Двухмерный контроль паритета
Двухмерный контроль паритета позволяет:
1. Обнаруживать и исправлять одиночные ошибки.
2. Обнаруживать двойные ошибки.
Способность приемника обнаруживать и исправлять ошибки называют прямым исправлением ошибок (Forward Error Correction, FEC). Двухмерный контроль паритета применяются в устройствах хранения данных. Такие методы При двухмерном контроле вычисляются множественные биты паритета четности.
Кодирование данных и передача по линии связи:
1. Данное, состоящее из (n∙m)-разрядов разбивается на n -фрагментов, состоящих из m -разрядов.
Например, данное, состоящее из 16-разрядов,  разбивается на 4 фрагмента длиной по 4 разряда (n = 4 фрагмента, m = 4 разряда).
разбивается на 4 фрагмента длиной по 4 разряда (n = 4 фрагмента, m = 4 разряда).
| Фрагмент 3 | Фрагмент 2 | Фрагмент 1 | Фрагмент 0 | ||||||||||||

| 
| 
| 
| 
| 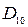
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
2. Фрагменты образуют прямоугольную матрицу, содержащую 4 строки и 4 столбца.
| J 3 | J 2 | J 1 | J 0 | |||
| I 3 | 
| 
| 
| 
| ||
| I 2 | 
| 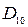
| 
| 
| ||
| I 1 | 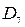
| 
| 
| 
| ||
| I 0 | 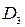
| 
| 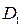
| 
| ||
где 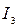 ,
, 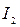 ,
,  ,
,  – номера строк;
– номера строк;  ,
,  ,
,  ,
,  – номера столбцов.
– номера столбцов.
Соответствие прямоугольной матрицы и исходного сообщения приведено в таблице.
| Фрагмент 3 (строка I3) | Фрагмент 2 (строка I2) | Фрагмент 1 (строка I1) | Фрагмент 0 (строка I0) | ||||||||||||

| 
| 
| 
| 
| 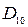
| 
| 
| 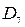
| 
| 
| 
| 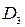
| 
| 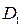
| 
|
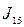
| 
| 
| 
| 
| 
| 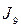
| 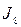
| 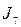
| 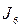
| 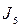
| 
| 
| 
| 
| 
|
3. Для каждой строки и столбца вычисляются биты паритета четности.
| J 3 | J 2 | J 1 | J 0 | PI | |
| I 3 | 
| 
| 
| 
| РI 3 |
| I 2 | 
| 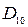
| 
| 
| РI 2 |
| I 1 | 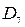
| 
| 
| 
| РI 1 |
| I 0 | 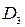
| 
| 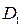
| 
| РI 0 |
| PJ | РJ 3 | РJ 2 | РJ 1 | РJ 0 | |
где РI 3, РI 2, РI2 , РI0 - паритеты строк; РJ 3, РJ 2, РJ 1, РJ 0 - паритеты столбцов.
4. Для всех битов паритета строк и столбцов вычисляется дополнительный бит паритета паритетов РIJ строк и столбцов паритета.
| J 3 | J 2 | J 1 | J 0 | PI | |
| I 3 | 
| 
| 
| 
| РI 3 |
| I 2 | 
| 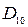
| 
| 
| РI 2 |
| I 1 | 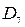
| 
| 
| 
| РI 1 |
| I 0 | 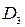
| 
| 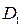
| 
| РI 0 |
| PJ | РJ 3 | РJ 2 | РJ 1 | РJ 0 | РIJ |
5. Из фрагментов и битов паритета, содержащих (n +1)∙(m +1)-разрядов, образуется сообщение:
 РI 3
РI 3  РI 2
РI 2 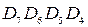 РI2
РI2  РI0 РJ 3 РJ 2 РJ 1 РJ 0 РIJ.
РI0 РJ 3 РJ 2 РJ 1 РJ 0 РIJ.
6. Передающий узел посылает по линии связи сообщение:
 РI 3
РI 3  РI 2
РI 2 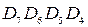 РI2
РI2  РI0 РJ 3 РJ 2 РJ 1 РJ 0 РIJ.
РI0 РJ 3 РJ 2 РJ 1 РJ 0 РIJ.
.
Прием и проверка данных:
1. Приемный узел принимает сообщение:
 РI 3
РI 3  РI 2
РI 2 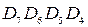 РI2
РI2  РI0 РJ 3 РJ 2 РJ 1 РJ 0 РIJ.
РI0 РJ 3 РJ 2 РJ 1 РJ 0 РIJ.
2. Сообщение разбивается на (n + 1) - фрагментов, состоящих из (m + 1) - разрядов:
| J 3 | J 2 | J 1 | J 0 | PI | |||||||
| I 3 | 
| 
| 
| 
| РI 3 | ||||||
| I 2 | 
| 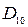
| 
| 
| РI 2 | ||||||
| I 1 | 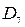
| 
| 
| 
| РI 1 | ||||||
| I 0 | 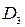
| 
| 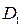
| 
| РI 0 | ||||||
| PJ | РJ 3 | РJ 2 | РJ 1 | РJ 0 | РIJ | ||||||
3. Для каждой строки вычисляются синдромы SI 3, SI 2, SI 1, SI 0, SР. Для каждого столбца вычисляются синдромы SJ 3, SJ 2, SJ 1, SJ 0, SР
| J 3 | J 2 | J 1 | J 0 | PI | SI | |
| I 3 | 
| 
| 
| 
| РI 3 | SI 3 |
| I 2 | 
| 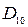
| 
| 
| РI 2 | SI 2 |
| I 1 | 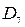
| 
| 
| 
| РI 1 | SI 1 |
| I 0 | 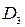
| 
| 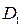
| 
| РI 0 | SI 0 |
| PJ | РJ 3 | РJ 2 | РJ 1 | РJ 0 | РIJ | SРIJ |
| SJ | SJ 3 | SJ 2 | SJ 1 | SJ 0 | SРJI |
3. Проверка на наличие ошибок:
- если все синдромы равны нулю, то ошибки нет;
- если синдром строки и синдром столбца содержат только по одной единице, то есть одна ошибка, которая находится на пересечении соответствующих строк и столбца.
Например, если синдромы SI 2 = 1 и РJ 0 =1, то на пересечении строки I2 и столбца J0 находится испорченный бит D8, который может быть исправлен.
| J 3 | J 2 | J 1 | J 0 | PI | SI | |
| I 3 | 
| 
| 
| 
| РI 3 | SI 3 |
| I 2 | 
| 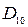
| 
| 
| РI 2 | SI 2 |
| I 1 | 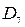
| 
| 
| 
| РI 1 | SI 1 |
| I 0 | 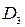
| 
| 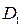
| 
| РI 0 | SI 0 |
| PJ | РJ 3 | РJ 2 | РJ 1 | РJ 0 | РIJ | SРIJ |
| SJ | SJ 3 | SJ 2 | SJ 1 | SJ 0 | SРJI |
- если обнаруживается более двух синдромов равных единице, то выявляется наличие множественных ошибок.
Например, если синдромы строк SI 2 = 1, SI 0= 1 и столбцов SJ 3 = 1, РJ 0 =1, то на пересечении строк I 2, I 0 и столбцов J 3, J 0 находятся биты  , D8,
, D8, 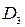 ,
,  ,которые не могут быть идентифицированы, а поэтому и исправлены.
,которые не могут быть идентифицированы, а поэтому и исправлены.
| J 3 | J 2 | J 1 | J 0 | PI | SI | |
| I 3 | 
| 
| 
| 
| РI 3 | SI 3 |
| I 2 | 
| 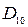
| 
| 
| РI 2 | SI 2 |
| I 1 | 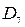
| 
| 
| 
| РI 1 | SI 1 |
| I 0 | 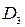
| 
| 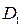
| 
| РI 0 | SI 0 |
| PJ | РJ 3 | РJ 2 | РJ 1 | РJ 0 | РIJ | SРIJ |
| SJ | SJ 3 | SJ 2 | SJ 1 | SJ 0 | SРJI |
Сборка исходного сообщения:
1. При отсутствии ошибки из принятого сообщения собирается исходное данное  .
.
2. При наличии одной ошибки:
- собирается исходное сообщение
 ;
;
- для синдромов SI 3, SI 2, SI 1, SI 0, SJ 3, SJ 2, SJ 1, SJ 0 в таблице приведены идентификаторы ошибок:
| Синдромы строк | Идентификатор ошибки строки | Синдромы столбцов | Идентификатор ошибки столбца | ||||||
| SI 3 | SI 2 | SI 1 | SI 0 | SJ 3 | SJ 2 | SJ 1 | SJ 0 | ||
| Ошибки нет | Ошибки нет | ||||||||
| Ошибка строки 0 | Ошибка столбца 0 | ||||||||
| Ошибка строки 1 | Ошибка столбца 1 | ||||||||
| Ошибка строки 2 | Ошибка столбца 2 | ||||||||
| Ошибка строки 3 | Ошибка столбца 3 |
Для синдромов SI 3, SI 2, SI 1, SI 0, SJ 3, SJ 2, SJ 1, SJ 0 рассчитывается идентификатор ошибки, который является номером N ошибочного бита данного:
N = 4∙ KI + KJ = 4∙ log2 (WI) + log2 (WJ),
где WI - вес синдромов строк SI 3, SI 2, SI 1, SI 0; WJ - вес синдромов столбцов SJ 3, SJ 2, SJ 1, SJ 0.
Например. Рассчитать номер ошибочного бита N для синдрома строк SI 3 SI 2 SI 1 SI 0 = 01002 = 410 и синдрома столбцов SJ 3 SJ 2 SJ 1 SJ 0 = 00012 = 110:
N = 4∙ log2 (410) + log2 (110) = 4∙ 2 + 0 = 8.
Получаем ошибку в восьмом бите  . Местонахождения ошибочного бита показано в таблице.
. Местонахождения ошибочного бита показано в таблице.
| Фрагмент 3 (строка I 3) | Фрагмент 2 (строка I 2) | Фрагмент 1 (строка I 1) | Фрагмент 0 (строка I 0) | ||||||||||||

| 
| 
| 
| 
| 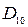
| 
| 
| 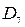
| 
| 
| 
| 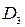
| 
| 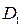
| 
|
| J 3 | J 2 | J 1 | J 0 | J 3 | J 2 | J 1 | J 0 | J 3 | J 2 | J 1 | J 0 | J 3 | J 2 | J 1 | J 0 |
Пример. Применить двухмерный контроль паритета для исходного сообщения 0001 0010 0100 1100.
Кодирование данных и передача по линии связи:
1. Сообщение разбивается на четыре фрагмента, для которых вычисляются паритеты четности
| J 3 | J 2 | J 1 | J 0 | PI | |
| I 3 | |||||
| I 2 | |||||
| I 1 | |||||
| I 0 | |||||
| PJ |
2. Передающий узел собирает из фрагментов сообщение 00011 00101 01001 11000 10111 и посылает его по линии связи.
Прием и проверка данных:
1. Приемный узел принимает сообщение 00011 00101 01001 11000.
2. Сообщение разбивается на фрагменты, для которых рассчитываются синдромы 0001 0010 0100 1100
| J 3 | J 2 | J 1 | J 0 | PI | SI | |
| I 3 | ||||||
| I 2 | ||||||
| I 1 | ||||||
| I 0 | ||||||
| PJ | ||||||
| SJ |
2. Выполняется анализ синдромов: все синдромы равны нулю, следовательно ошибок нет.
3. Исходное сообщение равно 0001 0010 0100 1100.
Прием и проверка данных (с одной ошибкой):
1. Приемный узел принимает сообщение 00011 00101 11001 11000.
2. Сообщение разбивается на фрагменты, для которых рассчитываются синдромы
| J 3 | J 2 | J 1 | J 0 | PI | SI | |
| I 3 | ||||||
| I 2 | ||||||
| I 1 | ||||||
| I 0 | ||||||
| PJ | ||||||
| SJ |
4. Расчет номера ошибочного бита N для синдрома строк SI 3 SI 2 SI 1 SI 0 = 00102 = 210 и синдрома столбцов SJ 3 SJ 2 SJ 1 SJ 0 = 10002 = 810:
N = 4∙ log2 (210) + log2 (810) = 4∙ 1 + 3 = 7.
Получаем ошибку в восьмом бите 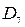 .
.
5. Восстановление данного 0001 0010 1100 1100.
6. Исправление ошибки, выполняется инверсией бита 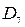 :
:
0001 0010  100 1100 = 0001 0010 0100 1100.
100 1100 = 0001 0010 0100 1100.
Код Хемминга
Помехоустойчивое кодирование методом Хемминга позволяет:
- обнаруживать одиночные ошибки;
- исправлять одиночные ошибки.
Метод основан на перекрестном вычислении битов паритета.
Основными свойствами кода Хемминга являются:
- расстояние по Хеммингу;
- минимальное расстояние по Хеммингу;
- вес Хемминга.
Расстоянием по Хеммингу d (x, y) называется число позиций, в которых различаются два n-разрядных кода.
Минимальным расстоянием d * называется наименьшее из всех расстояний по Хеммингу между различными парами всех n -разрядных кодов.
Весом Хемминга w (x) называется число ненулевых компонент n -разрядного кода.
Пример. Определить расстояние по Хеммингу d (x, y) для кодов х = 0110 и y = 1011:
| Код х | ||

| Сумма по модулю два | |
| Код y | ||
| Результат |
В результате 1101 единицы отражают число позиций, в которых различаются коды 0110 и 1011. Количество единиц равно 1 + 1 + 0 + 1 = 3.
Ответ. Расстояние по Хеммингу d (0110, 1011) = 3.
Пример. Определить минимальное расстояние d * для кодов 0110, 1011, 1101:
d (0110, 1011) = 3;
d (1011, 1101) = 2;
d (0110, 1101) = 2.
Ответ. Минимальное расстояние d * = 2.
Пример. Определить вес Хемминга w (x) для кода х = 0110.
Ответ. Вес Хемминга w (0110) = 0 + 1 + 1 + 0 = 2.
Помехоустойчивые коды характеризуется выражениями:
(n, k, d) или (n, k),
где n – общее число разрядов в передаваемом сообщении; k – число информационных разрядов (k = n - r); r – число проверочных разрядов; d * – минимальное кодовое расстояние между разрешенными кодовыми комбинациями.
Дополнительным показателями избыточности являются:
- относительная избыточность  ;
;
- относительная скорость передачи  .
.
Рассмотрим работу метода на примере кода Хемминга (7,4) для данного D 3 D 2 D 1 D 0 (n =7, k = 4).
Кодирование данных и передача по линии связи:
1. Вычисление для данного D 3 D 2 D 1 D 0 поверочных битов Р 2 Р 1 Р 0 по формулам:
Р 0 = D 2 Å D 1 Å D 0;
Р 1 = D 3 Å D 1 Å D 0;
Р2 = D 3 Å D 2 Å D 0.
2. Переда сообщения D 3 D 2 D 1 D 0 Р 2 Р 1 Р 0 по линии связи.
Прием и проверка данных:
1. Прием сообщения D 3 D 2 D 1 D 0 Р 2 Р 1 Р 0.
2. Вычисление синдромов  по формулам:
по формулам:
S 0 = D 2 Å D 1 Å D 0 Å Р 0;
S 1 = D 3 Å D 1 Å D 0 Å Р 1;
S 2 = D 3 Å D 2 Å D 0 Å Р 2.
Трёхразрядный код  называется синдромом.
называется синдромом.
Синдром представляет собой сочетание результатов проверки на чётность соответствующих символов кодовой группы и характеризует определённую конфигурацию ошибок (шумовой вектор).
3. Проверка на наличие ошибок:
- получение идентификаторов ошибки для синдромов  (восемь идентификаторов ошибки), приведенных в таблице.
(восемь идентификаторов ошибки), приведенных в таблице.
Таблица Идентификаторы ошибок
| № | Синдромы | Идентификатор ошибки | ||
| S 2 | S 1 | S 0 | ||
| Ошибки нет | ||||
| Ошибка в P 0 | ||||
| Ошибка в P 1 | ||||
| Ошибка в D 1 | ||||
| Ошибка в Р 2 | ||||
| Ошибка в D 2 | ||||
| Ошибка в D 3 | ||||
| Ошибка в D 0 |
Пример. Передать четырехразрядное данное D 3 D 2 D 1 D 0 = 0000 с контролем достоверности по Хеммингу.
Кодирование данных и передача по линии связи:
1. Вычисление для данного D 3 D 2 D 1 D 0 = 0000 поверочных битов Р 2 Р 1 Р 0 по формулам:
Р0 = D 2 Å D 1 Å D 0 = 0 Å 0 Å 0 = 0;
Р1 = D 3 Å D 1 Å D 0 = 0 Å 0 Å 0 = 0;
Р2 = D 3 Å D 2 Å D 0 = 0 Å 0 Å 0 = 0.
Поверочные биты Р 2 Р 1 Р 0 равны 000.
2. Передача сообщения D 3 D 2 D 1 D 0 Р 2 Р 1 Р 0 = 0000 000.
Прием и проверка данных:
1. Прием сообщения D 3 D 2 D 1 D 0 Р 2 Р 1 Р 0 = 0000 000.
2. Вычисление синдромов  :
:
S0 = D 2 Å D 1 Å D 0 Å Р 0 = 0 Å 0 Å 0 Å 0 = 0;
S1 = D 3 Å D 1 Å D 0 Å Р 1 = 0 Å 0 Å 0 Å 0 = 0;
S2 = D 3 Å D 2 Å D 0 Å Р 2 = 0 Å 0 Å 0 Å 0 = 0.
Синдромы  равны 000.
равны 000.
3. Проверка на наличие ошибок:
- из таблицы идентификаторов получаем, что для синдромов  = 0000 ошибки нет.
= 0000 ошибки нет.
Пример. Выполнить верификацию принятого сообщения 0100000, использующее кодирование методом Хемминга (7,4).
Прием и проверка данных:
1. Прием сообщения D 3 D 2 D 1 D 0 Р 2 Р 1 Р 0 = 0100 000.
2. Анализ принятого сообщения:
| Данное | Код Хемминга | |||||
| D3 | D2 | D1 | D0 | Р2 | Р1 | Р0 |
2. Вычисление синдромов  :
:
S0 = D2 Å D1 Å D0 Å Р0 = 1 Å 0 Å 0 Å 0 = 1 Å 0 Å 0 = 1 Å 0 = 1;
S1 = D3 Å D1 Å D0 Å Р1 = 0 Å 0 Å 0 Å 0 = 0 Å 0 Å 0 = 0 Å 0 = 0;
S2 = D3 Å D2 Å D0 Å Р2 = 0 Å 1 Å 0 Å 0 = 1 Å 0 Å 0 = 1 Å 0 = 1.
3. Проверка на наличие ошибок:
- для синдромов  = 101 из таблицы синдромов извлекаем сообщение: «Ошибка в D2».
= 101 из таблицы синдромов извлекаем сообщение: «Ошибка в D2».
4. Исправление ошибки:
- исправление ошибки с помощью логической операции инверсии  (второго разряда)
(второго разряда) 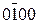 = 0000.
= 0000.
Ответ. Передавалось данное 0000.
Поиск по сайту: