Криптоанализ системы основанной на РСЛОС

Стандартный способ генерирования потока битов основан на использовании регистра сдвига с обратной связью. Это микросхема с ячейками памяти, в каждой из которых записан один бит информации. Множество таких ячеек и образует регистр. На каждом шаге содержимое нескольких заранее определенных ячеек, которые называются отводами пропускается через функцию обратной связи.

А ее значение записывается в самую левую ячейку регистра, сдвигая все остальные его биты на одну позицию вправо. Самый крайний справа, «вытолкнутый» из регистра, бит — выход регистра сдвига на данном шаге (рис. 1).

Рис. 1. Регистр сдвига с обратной связью

По причинам, о которых мы будем говорить позже, в качестве функций обратной связи желательно брать нелинейные функции. Однако это сложно осуществитьна практике, и поэтому пользуются регистром сдвига с линейной обратной связью или, сокращенно, РСЛОС, функция обратной связи в котором линейна. Этот регистр устроен так же, как и общий, описанный выше. Но в качестве функции обратной связи берется логическая операция XOR исключающего ИЛИ.

На языке математики работу регистра длины можно описать следующим образом. Задается последовательность битов , в которой на отводах стоят единицы, а в остальных ячейках — нули.

Допустим, что в начальном положении в регистре записана последовательность . На выходе регистра получается последовательность 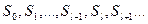, где при

Заметим, что если в начальном состоянии регистра во всех его ячейках стояли нули, то и на выходе мы будем получать сплошные нули.

Если же стартовая последовательность была нетривиальной, то генерируемая последовательность, в конечном счете, окажется периодической.

Действительно, число возможных последовательностей длины конечно, и меняя их на каждом шагу, мы волей-неволей получим одну из уже встречавшихся. После этого, ввиду детерминированности процесса, мы получим периодичность. Напомним, что периодом последовательности называется наименьшее натуральное число , при котором для всех достаточно больших значений параметра выполняется равенство .

Нетрудно подсчитать, что существует 2 -1 разных ненулевых начальных состояний регистра. Поэтому максимум, на что можно рассчитывать, это на то, что регистр сдвига с линейной обратной связью при любом ненулевом начальном положении будет генерировать последовательность битов периода 2 -1. Свойства выдаваемой РСЛОС последовательности тесно связаны со свойствами двоичного многочлена

,

ассоциированного с этим регистром. Его ненулевые коэффициенты называются отводами, как и соответствующие ячейки регистра, поставляющие значения аргументов функции обратной связи. На рис. 2 изображен РСЛОС, ассоциированный с многочленом , а на рис. 3 – с многочленом .

Рис. 2. Регистр сдвига с линейной обратной связью для ассоциированного многочлена

Свойства последовательности битов, генерируемой РСЛОС зависят от ассоциированного многочлена:

1. Если старший коэффициент ассоциированного многочлена , то периодичность генерируемой последовательности может проявиться не сразу.

2. Если = 1, то соответствующая последовательность называется неособой. Она будет периодичной с самого начала, т.е. равенство выполнено для всех , а не только для достаточно больших.

Рис. 3. Регистр сдвига с линейной обратной связью для ассоциированного многочлена

Наиболее интересны неособые последовательности, соответствующие многочленам со следующими дополнительным свойством: когда неприводим, при любом ненулевом начальном состоянии регистра период генерируемой последовательности равен наименьшему числу , при котором многочлен делит 1 . Как следствие, период последовательности будет делить число 2 -1.

Поиск по сайту: