Математические модели открытого текста

Потребность в математических моделях открытого текста продиктована, прежде всего, следующими соображениями. Во-первых, даже при отсутствии ограничений на временные и материальные затраты по выявлению закономерностей, имеющих место в открытых текстах, нельзя гарантировать того, что такие свойства указаны с достаточной полнотой. Например, хорошо известно, что частотные свойства текстов в значительной степени зависят от их характера. Поэтому при математических исследованиях свойств шифров прибегают к упрощающему моделированию, в частности, реальный открытый текст заменяется его моделью, отражающей наиболее важные его свойства. Во-вторых, при автоматизации методов криптоанализа, связанных с перебором ключей, требуется “научить” ЭВМ отличать открытый текст от случайной последовательности знаков. Ясно, что соответствующий критерий может выявить лишь адекватность последовательности знаков некоторой модели открытого текста.

Один из естественных подходов к моделированию открытых текстов связан с учетом их частотных характеристик, приближения для которых можно вычислить с нужной точностью, исследуя тексты достаточной длины (см. Приложение1). Основанием для такого подхода является устойчивость частот -грамм или целых словоформ реальных языков человеческого общения (то есть отдельных букв, слогов, слов и некоторых словосочетаний). Основанием для построения модели может служить также и теоретико-информационный подход, развитый в работах К.Шеннона [Шен63].

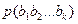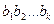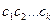Учет частот -грамм приводит к следующей модели открытого текста. Пусть представляет собой массив, состоящий из приближений для вероятностей появления -грамм в открытом тексте, , — алфавит открытого текста, Тогда источник “открытого текста” генерирует последовательность знаков алфавита , в которой -грамма появляется с вероятностью , следующая -грамма появляется с вероятность и т. д. Назовем построенную модель открытого текста вероятностной моделью -го приближения.

Таким образом, простейшая модель открытого текста – вероятностная модель первого приближения – представляет собой последовательность знаков , в которой каждый знак появляется с вероятностью , независимо от других знаков. Будем называть также эту модель позначной моделью открытого текста. В такой модели открытый текст имеет вероятность .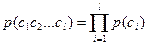

В вероятностной модели второго приближения первый знак 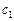имеет вероятность , а каждый следующий знак зависит от предыдущего и появляется с вероятностью

,

где 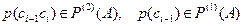, . Другими словами, модель открытого текста второго приближения представляет собой простую однородную цепь Маркова. В такой модели открытый текст имеет вероятность .

Модели открытого текста более высоких приближений учитывают зависимость каждого знака от большего числа предыдущих знаков. Ясно, что чем выше степень приближения, тем более “читаемыми” являются соответствующие модели. Проводились эксперименты по моделированию открытых текстов с помощью ЭВМ.

Приведем примеры “открытых текстов”, выработанных компьютером на основе частотных характеристик (алфавита со знаком пробела) собрания сочинений Р.Желязны объемом 10652970 байтов:

1. (Позначная модель) ались проситете пригнуть стречи разве возникл;

2. (Второе приближение) н умере данного отствии официант простояло его то;

3. (Третье приближение) уэт быть как ты хоть а что я спящихся фигурой куда п;

4. (Четвертое приближение) ество что ты и мы сдохнуть пересовались ярким сторож;

5. (Пятое приближение) луну него словно него словно из ты в его не полагаете помощи я д;

6. (Шестое приближение) о разведения которые звенел в тонкостью огнем только.

Как видим, тексты вполне “читаемы”.

Отметим, что с более общих позиций открытый текст может рассматриваться как реализация стационарного эргодического случайного процесса с дискретным временем и конечным числом состояний ([Гне88]).

Поиск по сайту: